3-11 바이아스가 추가된 Quadratic Hypothesis Perceptron에 의한 XOR 논리 처리
선형 hypothesis를 사용하는 단일 퍼셉트론에 의해서 XOR 논리 처리 결과 hypothesis 출력 값이 분류가 불가능한 0.5 의 값이 항상 얻어진다. 이에 대한 궁극적인 해결책으로 NN(neural network) 기법이 제시되었지만, 이와는 달리 전통적인 linear regression 기법을 탈피하여 quadratic regression 기법을 적용해 보기로 한다.
NN 기법이든 quadratic hypothesis 기법이든 간에 기법이 중요한 것이 아니라 주어진 문제를 해결하기 위해서 충분한 수의 웨이트 벡터가 필요한 것이다. 여기서 소개하는 quadratic regression 기법은 이미 2차 방정식의 2개의 실근을 구하는 문제 해결에 탁월한 성과를 보여 주었으며 다시 XOR 문제의 특성에 맞춰 hypothesis를 구성해 보기로 한다.
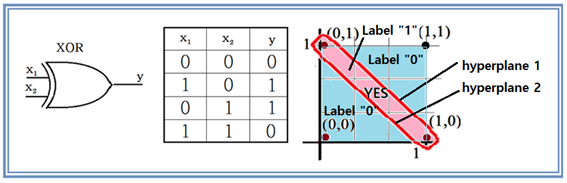
배타논리는 그림에서처럼 x1 이나 x2 2개 중의 1개만이 “1”일 때에 출력 y가 “1”이 된다. 좌표 평면에서 관찰해 보면 (-0,0) 과 (1,1) 이 “0”이며 (1,0)과 (0,1) 이 “1”이 되므로 서로 교차하는 위치에 있으므로 분리선을 긋기가 불가능하다. 쉽게 말하자면 (1,0)과 (0,1)을 분리해 내려면 그림에서처럼 적어도 2개의 hyperplane 이 필요한 것이다.
전통적인 linear regression 기법을 사용할 때의 hypothesis는 다음과 같이 W 또는 b 에 대해서 1차식 형태로 설정한다.
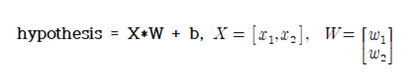

벡터 X 에 대해서 0.5 의 값을 주기 때문에 HIGH 또는 LOW 로 논리 값을 분별해 내기가 곤란해진다.
지금부터는 일차식 형태의 hypothesis 가 제대로 분리선을 학습해 내지 못하므로 웨이트를 늘려 보기로 한다. 첫 번째 은 그대로 사용하면서 랜덤한 바이아스 하나를 도입하여 quadratic hypothesis를 구성하여 시험해 보자.
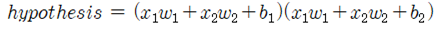

TensorFlow 학습을 위한 데이터 구조는 아무런 변동 없으며 단지 hypothesis 와 cost 함수만 바꾸어 주도록 한다.

learning_rate 값은 0.05 로 두고 학습 횟수를 500회로 설정하여 파이선코드 quadratic_regression_XOR_bias_01.py를 실행 해보자. 다음의 결과는 500회 반복계산을 시행한 학습결과이다. 결과를 자세히 관찰해 보면 100회 학습을 통해서도 약 0.2% 정도의 오차로 충분히 수렴된 결과를 보여준다. 하지만 때때로 hypothesis 값들이 0.5가 되는 즉 불완전한 hypothesis 설정에 따라 머신 러닝이 실패하는 경우도 자주 일어난다.
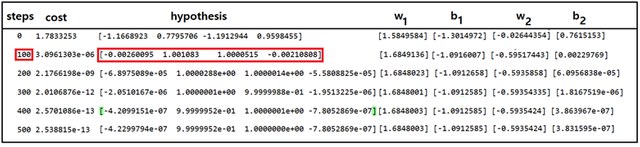
즉 바이아스를 하나 더 추가한 현재의 quadratic hypothesis 사용에 있어서 제대로 XOR 논리를 학습한 경우와 반면에 XOR 논리처리가 불가능한 경우 2 종류의 결과가 교대로 출력될 수 있다는 점이다. 실제로 코드를 많이 실행해본 결과 흥미롭게도 XOR 로직 해를 계산하는 경우와 그렇지 않은 경우와의 비율은 거의 50:50 임을 알 수 있다.
결국 이러한 문제를 해결하기 위해서는 웨이트를 더 추가해야 할 필요가 있을 것이다.
#quadratic_regression_XOR_bias_01.py
import tensorflow as tf
tf.set_random_seed(777)
x1_data = [0., 1., 0., 1.]
x2_data = [0.,0.,1.,1.]
y_data = [0., 1., 1., 0.]
#placeholders for a tensor that will be always fed.
x1 = tf.placeholder(tf.float32)
x2 = tf.placeholder(tf.float32)
Y = tf.placeholder(tf.float32)
w1 = tf.Variable(tf.random_normal([1]), name='weight1')
w2 = tf.Variable(tf.random_normal([1]), name='weight2')
b1 = tf.Variable(tf.random_normal([1]), name='bias1')
b2 = tf.Variable(tf.random_normal([1]), name='bias2')
hypothesis = (x1 * w1 + x2 * w2 + b1)*(x1 * w1 + x2 * w2 + b2)
#cost/loss function
cost = tf.reduce_mean(tf.square(hypothesis - Y))
#Minimize. Need a very small learning rate for this data set
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.05)
train = optimizer.minimize(cost)
#Launch the graph in a session.
sess = tf.Session()
#Initializes global variables in the graph.
sess.run(tf.global_variables_initializer())
for step in range(501):
cost_val, hy_val, _ = sess.run([cost, hypothesis, train],
feed_dict={x1: x1_data,x2: x2_data, Y: y_data})
if step % 100 == 0:
print(step, cost_val, hy_val,sess.run(w2),sess.run(b2),sess.run(w1),sess.run(b1))
짱짱맨 호출에 응답하여 보팅하였습니다. 꾸준한 활동을 응원합니다.
북이오(@bukio)는 창작자와 함께 하는 첫번째 프로그램을 만들었습니다. 이를 위해 첫번째 길드(Guild) 구성을 위한 공지글을 게시하였습니다. 영문 문학작품의 한글 번역에 관심이 있는 분들의 많은 참여를 바랍니다. 고맙습니다.