(고등수학)원의 방정식
원의 접선의 방정식에 대해서 알아보자.
원의 접선의 방정식
접점의 위치를 알 때,
원과 접선이 만날때의 접점의 위치를 알때 원과 접하는 접선의 방정식을 알 수 있는 방법이 있다.
(기본형) 원의 방정식 = x²+y²=r² 선의 방정식 = y=mx+b
원과 만나는 점을 ( x₁, y₁) 이라고 해보자.
그림으로 그려봤다.
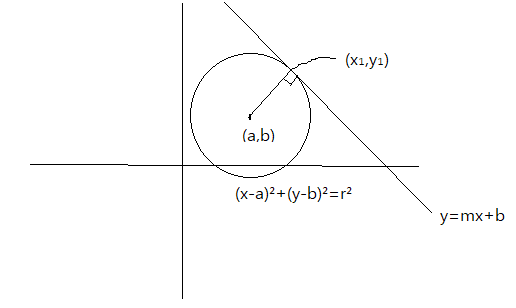
참고) (x-a)²+(y-b)²=r² 은 x와 y가 원위의 점을 의미하기 때문에
(x₁-a)²+(y₁-b)²=r² 이라고도 할 수 있다.
(앞으로 참고)는 cf)로 표시한다.)
원의 중심 (a,b)의 위치와 접점의 위치 (x₁,y₁)을 알고 있기 때문에 점과 점사이의 위치관계를 이용하여 기울기를 구할 수 있다.
기울기 = y증가량/x증가량 이다.
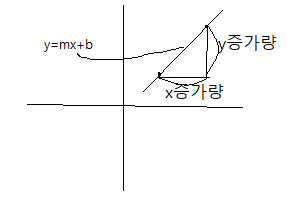
기울기는 선의 방정식의 기본형인 y=mx+b에서 m을 나타낸다.
원의 방정식의 원의 중심의 위치와 반지름 그리고 선의 방정식의 접점의 위치와 기울기를 알고있게 된다.
기울기와 점의 위치를 알고 있다면 간단히 직선의 방정식을 구할 수 있다.
점의 위치를 (x₁ , y₁) 이라고하고 기울기를 m 이라 할 때
직선의 방정식은 y-y₁ = m (x-x₁) 이 된다.
원의 중심을 (0,0)이라 하고 기본형 x²+y²=r²과 기울기와 점의 위치를 알 때의 직선의 방정식을 이용해서 식을 구해보면
원의 중점과 접점의 기울기 = y₁-0/x₁-0 이 되므로 m = y₁/x₁ 이 된다.
원의 중심에서 뻗은 선이 접선의 접점과 만나는 선은 서로 수직이고 수직이 되는 선은 서로 mm′=-1이 된다는 성질을 이용하면
접선의 방정식의 기울기는 -x₁/y₁이 된다. cf) m과 m′은 수직선끼리의 기울기이다.
그대로 위의 식의 m에 대입해보면
y-y₁ = -x₁/y₁ (x-x₁) 이라는 식이 나온다. 이 식을 정리해주면
y-y₁ = -x₁x/y₁ + x₁²/y₁ 이 되며 이항해주면 y = -x₁x+x₁²/y₁ + y₁ 이 된다.
간단히 해주기 위하여 y₁을 각 항에 곱해주면 y₁y = -x₁x+x₁² + y₁²
이항해 주면 y₁y +x₁x = -x₁x+x₁² + y₁² 가 되고 다시 정리해주면
x₁x + y₁y = x₁² + y₁² 이 된다. 원 위의 접점이 (x₁ , y₁) 이므로
x² + y² = r² 에서 x 와 y가 원 위의 점을 나타내므로 x₁과 y₁을 대입해주면 x₁² + y₁² = r² 이 된다.(r=반지름)
그러므로 x₁x + y₁y = r² 이 되는 것이다.
이런식을 원과 접선의 접점을 알때의 접선의 방정식을 구하는 식이 도출된다.
(본 글의 수정되어야할 부분은 알려주신다면 수정하겠습니다.)