MATHEMATICS IN TECHNOLOGY AND DAILY LIFE: Importance Of Mathematical Concept.
Million years ago, mathematics is one of the vital and most effective instrument that people use in daily life, especially scientists who use mathematical concept to derive and implement some equation and machine respectively for easy evaluation. Nowadays, most student would like to know why they have to study various mathematical concepts. 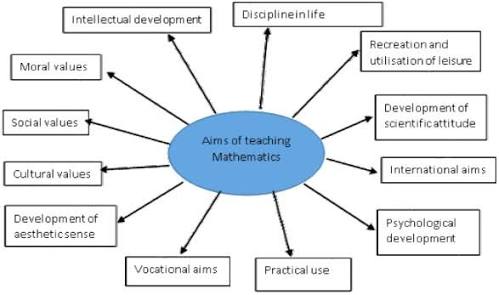.jpg) They believe mathematics has no real-life application but just to know the formula and apply it only in classroom. When teachers try to convince their students that mathematics is useful in many professions, such as engineering and medical sciences, many of these student may not be interested in these occupations. Some student wanted to be a computer game designers instead, but the wrongly believe that this profession did not require mathematics. Other students aspired to be soccer players but they did not realise that the sport could involve some mathematics.
They believe mathematics has no real-life application but just to know the formula and apply it only in classroom. When teachers try to convince their students that mathematics is useful in many professions, such as engineering and medical sciences, many of these student may not be interested in these occupations. Some student wanted to be a computer game designers instead, but the wrongly believe that this profession did not require mathematics. Other students aspired to be soccer players but they did not realise that the sport could involve some mathematics.
However, there are still many jobs that may not require much mathematics, except perhaps, for simple arithmetic like counting money and telling time, e.g., actor and actresses, taxi drivers, administrators and language teachers. How often do they use, for example, Algebra, in their workplace? Why study so much mathematics when many adults do not even use it in their professions? Isn't it a waste of time and resources? But mathematics involves not just concepts and procedural skills but also thinking processes. It can be concluded that "mathematics is the queen of science", mathematical cognitive and metacognitive processes, such as investigation proficiency, problem solving strategies, communication skills and critical and creative thinking, are important in and outside the workplace in our daily life
THE PURPOSE OF MATHEMATICS.
In ancient times, mathematical practices were divided into scientific mathematics and subscientific mathematics;the former being mathematical knowledge pursued for its own sake without any intentions of applications; and the latter being specialists’ knowledge that was applied in jobs such as architects, surveyors and accountants. Subscientific mathematics was often transmitted on the job and not found in books, but in modern days where mathematics is divided into PURE and APPLIED mathematical knowledge, the latter is usually taught at higher levels in schools because of the utilitarian ideology of the industrial trainers and the technological pragmatists who argue that schools should prepare students for the workforce (Ernest, 1991). However, groups with a PURIST ideology believe in studying mathematics for its own sake. For example, the old humanists advocate the transmission of mathematical knowledge because of their belief that mathematics is a body of structured pure knowledge, while the progressive educators prefer to use activities and play to engage students so as to facilitate self-realisation through mathematics because of their belief in the process view of mathematics and child-centreness. There is a third type of ideology called the SOCIAL change ideology of the public educators who wish to create critical awareness and democratic citizenship via mathematics through the use of questioning, discussion, negotiation and decision making.
However, the needs of the society may differ from the desires of individual students: the latter may not be interested to learn mathematics partly because they do not see the use of it, especially when most applications in the workplace are beyond their level, and partly because they may not be interested in professions that require a lot of mathematics. Therefore, there is a need to convince these students why they still need to study mathematics (and other subjects) which they may not need in their future working life.
AIM OF MATHEMATICS.
The aims of teaching and learning mathematics are to encourage and enable students to:
a. Recognize that mathematics permeates the world around usappreciate the usefulness, power and beauty of mathematics
b. Enjoy mathematics and develop patience and persistence when solving problems
c. Understand and be able to use the language, symbols and notation of mathematics
d. Develop mathematical curiosity and use inductive and deductive reasoning when solving problems
e. Become confident in using mathematics to analyse and solve problems both in school and in real-life situations
f. Develop the knowledge, skills and attitudes necessary to pursue further studies in mathematics
g. Develop abstract, logical and critical thinking and the ability to reflect critically upon their work and the work of others
h. Develop a critical appreciation of the use of information and communication technology in mathematicsappreciate the international dimension of mathematics and its multicultural and historical perspectives.
APPLICATION OF MATHEMATICS
Algebra
Computer Science
Cryptology (and the Protection of financial accounts with encrypted codes)
Scheduling tasks on processors in a heterogeneous multiprocessor computing network
Alteration of pattern pieces for precise seam alignment
Study of crystal symmetry in Chemistry (Group Theory)
Differential Equations and Fourier Analysis
Most of Physics and Engineering (esp. Electrical and Mechanical)
Sound waves in air; linearized supersonic airflow
Crystal growth
Cryocooler modeling
Casting of materialsMaterials science
Electromagnetics analysis for detection by radar
Probability and Statistics
Calculation of insurance risks and price of insurance
Analysis of statistical data taken by a census
Reliability and uncertainty of large scale physical simulations
Speech recognitionSignal processing
Computer network design
Tracking and searching for submarines
OTHERS ARE;
Carpentry (e.g., scale factor, isoclines/lines of constant elevation, angular measurement and conversions, calculations with decimals and fractions, converting distance and direction into latitudes and departures)
Construction Technology (e.g., unit conversions, Pythagorean theorem, sampling methods, right- triangle trigonometry, volume of cylinders)
Site Layout (e.g., angles and geometric figures; powers and square roots; unit conversions for lengths, areas and volumes; interpreting drawings)
Project Supervision (e.g., bar graphs, network diagrams, rates of productivity).