Understand The deep Q learning method : an usefull technic for AI
Understand The deep Q learning method : an usefull technic for AI
Foreword
One of the most popular models in the deep reinforcement-learning sub-branch is the algorithm called Deep Q Network or DQN. Understanding this method is extremely important. It is the basis of many deep reinforcement-learning algorithms. The DQN model was first proposed by researchers at Google DeepMind in 2013 in a paper called Playing Atari with Deep Reinforcement Learning. In it, they described the DQN architecture and explained why this method was so effective especially for Atari games.
In this period, it is no exaggeration to say that the DQN method appeared in a good time. Indeed, other methods based on the Q function had made it possible to advance in the field of reinforcement learning. However, researchers remained at an impasse. At the same time, the tabular Q-learning method was on the rise and had solved some problems regarding the accumulation of states in reinforcement problems. Despite everything, it was not very effective in the context of observation of large ensembles. Therefore, from there to evoking a solution for the resolution of video games, it was inconceivable. The complexity was too great for them. Having to read all of the pixels and their states was inconceivable. The algorithms would have had too many states to consider. Tests have shown that the available reinforcement methods did not even come close to a satisfactory solution.
Especially since in some environments the number of observations is almost endless. Quickly, it was necessary to decide on the ranges of parameters to be taken into account to distinguish the crucial states from those that are not relevant. For a video game, a single pixel will not make a difference in a game. It is therefore possible to create a larger assembly as part of the image as a state. However, even so, it is necessary to be able to distinguish areas of the screen where the action is relevant to the sequence of events. One solution in this case has been to provide both a state and an action mapped into a single value. In machine learning, we talk about a regression problem. There are several concrete ways to represent and train this type of representation.
Here we will describe one of them. Because of its efficiency and its ease in spreading over different problems, the Deep Q Network has become essential for reinforcement learning.
The genesis of DQN
Remember that the goal of reinforcement learning as a whole is to find the optimal policy that will give us the maximum return. In order to calculate this policy, we first start by calculating the emblematic function of the DQN method, the Q function.
Recall that the function Q is the function of value and state. It indicates the value of a state-action pair. Its use allows us to use the result obtained by the agent starting from a state s and executing the action “a” following a policy π.
In the case of the DQN method, we have to calculate the set of state-action values with the Q function. However, in some cases it can be extremely long and complicated to calculate the Q-value of each action-state pair. Instead of calculating Q values iteratively, we can use one of the many approximation functions. Here in the context of the DQN, it will be with a neural network that we will do. In this way, we can then parameterize our function Q with a parameter theta and calculate the Q value with parameter theta. We just feed the state of our environment into a neural network and it will return the Q value of all possible actions from that state. Once the Q values are found, we can select the best action like the one with the maximum Q value. Since we are using a neural network to approximate the Q values, the neural network is called the Q network. Since most of the time we are dealing with a deep neural network to approximate the Q value, then our deep neural network is called a deep Q network or DQN. Now you know all about the genesis of DQN. However, at this point, many questions remain unanswered. Let us try to take it one step further.
The interactions with the environment
Before going into details about the DQN method, it is important to review the agent's interactions with its environment. We know that for the agent it is necessary to interact with the environment in order to receive rewards but also data for training. We can act randomly as is done in some cases. But in the context of a video game, for example, is it really relevant? What is the probability of winning in this scenario? It's very rare. So it will take several games before you achieve enough success. An alternative would be to use our approximate Q function as a source of behavior. We find the principle mentioned in the context of the iterative value method.
If our representation of Q is good, then the experience we get from acting on the environment will show us that the agent's data is valid for training. In a low-quality approximation, we detect it by experience. The concern here is that our agent can get caught up in bad deeds without trying to behave differently. We return to our dilemma of exploitation - exploration. It is important to give the agent the opportunity to explore the environment and build a series of transitions and actions with various outputs. Even though we should not let it act in just any manner, we are above all looking for efficiency. For example, it would be silly to reproduce actions whose sequence has already been presented and did not yield any interesting data.
Research has shown that an initially randomized system, when the approximation cannot be used, is very often an interesting alternative since it provides a basis that offers sufficient and varied interactions with the environment. Eventually, as our training system progresses, the randomized behavior becomes ineffective and we can model our approximation Q and choose what action to take. This one proposing with our training, a more serious approximation.
A method that applies this proposition very well is the ϵ-greedy method. It will simply alternate between a random phenomenon and the policies of Q by using the hyper parameter ϵ. By varying ϵ, we choose the part of randomness in our actions. We start in practice with ϵ = 1.0, to gradually end around a value varying between 0.05 or 0.02 depending on the case. This method helps both to explore the environment at the start of the experiment, but also to maintain a good policy afterwards by switching to the Q function. There are other solutions to deal with the subject of exploration and exploitation. However, that will not be our subject here.
How to train a network in deep Q Learning ?
This is a question we can legitimately ask ourselves. Truthfully speaking, the good training of the network provides the quality of the results of the algorithm. So let us see the researchers' proposal on this subject.
Recall that we run our algorithm with the network parameter θ. Its initial value is random in order to be able to start approaching the optimal Q function. Since we are in the phase of initializing the function, the result will never be optimal. We are therefore going to train the network over several iterations. We try by this principle to find the optimal parameter θ. Once the optimal parameter θ has been found, we will have the optimal Q function. Then we can extract the optimal policy from the optimal Q function.
One of the most popular solutions to find optimal θ and Q is the use of a deep neural network. We find this approach especially in the context of representation associated with images on the screen.
The training data:
The basis of Q-learning is borrowed from the supervised machine learning model. Indeed, we are trying to work with a complex nonlinear function, in our case Q with a neural network. To do this we have to calculate targets for the function using the Bellman equation to claim to have a supervised learning problem at hand. This is a good idea, but to use an optimization SGD (the little name behind this technique), our training data must be independent and identically distributed (I.I.D principle).
In our case, our data does not agree with this principle. To remedy this, we can use a buffer in which we record our past experiences and our training samples. This collection will replace the latest experiments. We are talking about the replay buffer technique. We use this buffer called replay buffer to collect the agent's experience. The replay buffer will simply serve as a collection of experiences that we set aside to use for training. From there, based on that experience, we train our network.
Replay buffer :
This tuple in our replay buffer, also called in French, experience buffer. We usually denote it with D. This information transition is what is trivially called the agent experience. The idea of using a buffer to store user experience is interesting since we train our DQN with the experience we sampled in the buffer.
In this way, we collect the agent's transition information during several episodes and we save it in the replay buffer. Transition information is stored in a stack (our replay buffer) where the newly entered data will be added to the bottom of the stack. However, this method has a disadvantage. In fact, we are going to store the experiences here one by one. From experience to experience, these will often be similar. To avoid this, we can integrate some random transition into the replay buffer before training the network.
Remember that the replay buffer has a storage limit, and can therefore only keep a certain number of agent experiences. When this is filled, the new entries overwrite the old ones. The replay buffer is generally constructed like the structure of a queue. That is, so that the first entries are the first exits. Therefore, each addition after the full battery will eliminate the oldest experience and make room for the new one. At the same time, this allows the sample replay buffer to be improved. The further we go in training, the better the experiences tend to be.
Using the loss function, a great ally:
In our DQN method, we want to predict the values of Q. Now, these are continuous values. This will add complexity to the prediction. To overcome this, we use in DQN a regression task. The most popular method is the mean squared error, also noted MSE. It will come to play the role of loss function during the regression. The principle of the MSE can be translated as the squared average of the difference between the target value and the predicted value, we note that as follows:
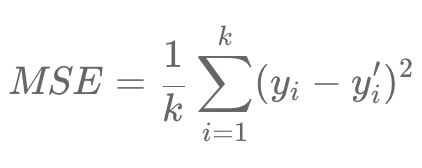
Where y plays the role of target value, y " of the predicted value and K the number of training samples.
Our goal is to train our network and try to minimize the MSE between the target Q value and the predicted Q value as much as possible. Obviously, the goal is to get the optimal Q value, which also comes down to minimizing error. Since the difference between the target Q value and the current Q value tends towards 0 as one approaches the optimal Q value. We use the Bellman equation for this. You will find an article covering the concept of this equation here. We know that the optimal Q value can be obtained using the Bellman Optimal equation:
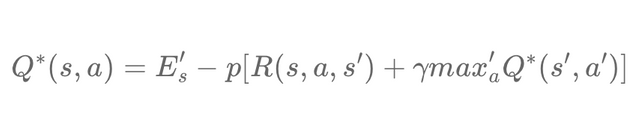
Where R (s, a, s ’) represents the immediate reward r, obtained by performing an action in state s leading to state s’. It is therefore possible to replace R (s, a, s ’) simply by r.
In our equation, we can also remove the expected factor E. Indeed, we will approximate this factor by taking a sample of K transitions from the replay buffer and recovering an average value. Thus according to the optimal Bellman equation, the optimal value Q is the sum of the rewards to which we add the maximum value Q reduced to the next action-state pair:
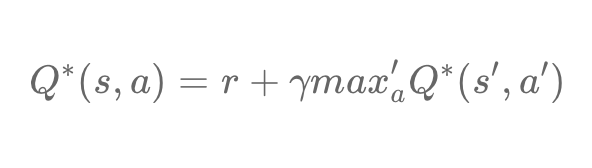
We can also define our loss as the difference between the target value (the optimal Q value) and the predicted value (the Q value predicted by DQN). The loss function will then be expressed:
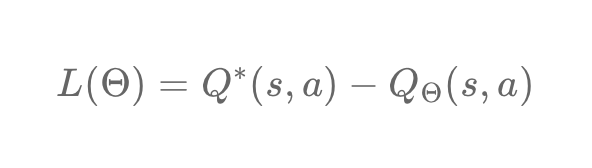
By substituting the above equation for the previous one, we get this simplified formula:
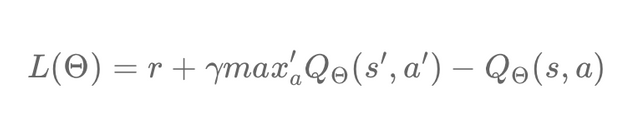
We calculated the predicted Q-value using the network parameter θ. Now let's see how to calculate the target value. We have seen that it is the sum of the rewards to which we add the maximum Q value reduced to the next action-state pair.
Similar to the predicted Q-value, we can calculate the Q-value of the next action-state pair by using the same network parameter, θ. Indeed, notice in our equation that we have, the two values Q parameterized by θ.
Instead of calculating the loss as just the difference between the target Q value and the predicted Q value, we use the MSE method as the loss function. Remember that we have our experiences stored in the replay buffer. In addition, we have a small part of our randomized sample. We then train the network and try to minimize the MSE. We can then translate our loss function as follows:
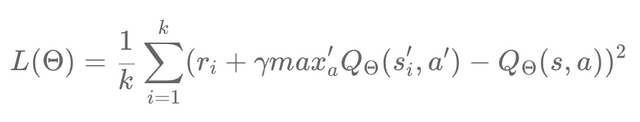
We have seen that the target value is simply the sum of the rewards and the maximum Q value reduced to the next action-state pair. Consider the case where state s is the terminal state. If s is the last step in an episode, then we cannot calculate the Q value, since we have no action to take in the terminal state. In this case, the target value will become our reward. Therefore, our loss function will look like:
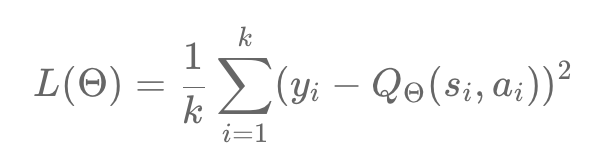
We have trained our network by minimizing the loss function. However, we have seen that it is also possible to minimize the loss function by finding the optimal parameter θ. To do this, we can use the gradient descent method and find the optimal parameter θ (how can we reduce the MSE with the gradient descent?).
Correlation between stages:
Another problem with our Q-learning model concerns its training procedure. By default, it is based on a method that does not respect the i.i.d principle. The Bellman equation gives us values of Q (s, a) in direct relation to Q (s ’, a’) (we speak of bootstrapping). The concern being that between s and s, only one step has passed. This makes s and s very similar, too similar in fact. This makes their differentiation very difficult for the neural networks. So when we optimize our neural network parameters, to achieve a Q (s, a) value close to the desired result, we can quickly alter the value of Q (s ’, a’) with each iteration. This will make our training very unstable. We have an error propagation which can completely destroy our approximation of Q (s, a).
There is a trick to solve this problem. We can build a new network playing the role of the target. With this, we create a copy of our network that we will use for Q (s ’, a’) in the Bellman equation. This network is synchronized with the main network. We regularly and periodically synchronize the two networks. At every N step with N that will become one of DQN's hyperparameters, often between 1k and 10k.
The target network to the rescue
Despite the steps already taken, we continue to have a little problem with our loss function. We know that the target value is the sum of the rewards plus the reduced maximum Q value at the next state-action pair. We calculate this Q value on the target and we predict the Q value using the same parameter θ. Now we have a problem since the target and predicted value both depend on the same parameter, in this case θ. This can cause instabilities when using the MSE and the networks will learn in a bad manner. It also causes a lot of discrepancy in training.
How can we avoid this? It is possible to freeze the target value for a time and calculate only the predicted value. To do this, we introduce another neural network called target network to calculate the Q value of the next state-action pair. The parameter of the target network is denoted θ '. Therefore, our main Q network will calculate the predicted Q values and learn the optimal θ parameter using the gradient descent method. The target network will be put on standby for a while in order to, after a period, resume operation and update the parameter θ ' by simply copying the parameter θ from the main network. We start to freeze the target network and so on. In this case, our loss function becomes:
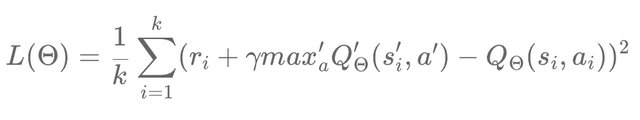
The Q value of the next action state is calculated by the target network with the parameter θ 'and the predicted Q value is calculated by the main network with the parameter θ. If we go back to our simplified notation, we get:
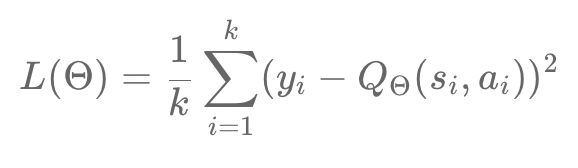
The Markov property applied to Deep Q Learning
Our DQ-learning method uses the formalism of the Markovian decision process. Which in principle specifies that the model obeys the Markov properties: According to this, the observations of the environment are all distributed in an optimal way. That is, each observation allows us to distinguish the entirety of the states. By analyzing a single image from a video game, we cannot retrieve all of the information. For example, the speed or direction of an object will not be known. This invalidates the Markov properties. Therefore, our system, in the case of video games, is relegated to the rank of Partial Markovian or MDPS or POMDPS decision process. We speak of POMDPS when we have a model with a Markovian decision process that does not respect the Markov properties. This method appears very regularly in a real context, such as in card games where the opponent's hand is unknown. There is a way to turn a POMDPS into an MDP.
Results
After introducing so much new information and technical mathematical concepts, let us go back to the key elements for the DQN model.
First, we update the general lattice parameter θ with a random value. We have learned that the target network is a simple copy of the general network. Then we update the parameter θ ' by copying the parameter θ. We also update D, our replay buffer.
Now for each step in an episode we add the state of the environment in our network, and we get its outputs corresponding to the Q values for all possible actions in the state. Then we choose the action, which has the maximum Q value.
If we only select the stock with the highest Q value, then we don't explore other new stocks. To avoid this, we select our stocks by adding the ϵ-greedy policy. We select our random action with an epsilon probability and with the probability ϵ-1, we select the best action with the maximum Q value.
Since we update our lattice parameter θ with a random value, the action we select by taking the maximum Q value will not necessarily be the optimal action. But that's okay, we're just improving the selected action. We then go to the next state and get the reward. If the action is good then we will receive a positive reward, otherwise, it will be negative. We store this information in replay buffer D.
Then, in a random manner, we create a sample of K of transitions coming from the replay buffer for which we have previously calculated the loss parameter. Our loss function is given by:
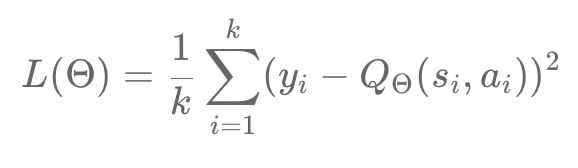
During the first iterations, the loss will be very high since our parameter θ of the network is configured randomly. To minimize the loss, we calculate the gradients of the losses and we improve our network parameter θ by following the principle of the gradient descent.
We do not change the target network parameter θ' at each step. We freeze the parameter θ' for several steps and then we inject the value of θ into θ'. We repeat this process for several episodes to approximate the optimal Q value. Once the optimal Q value is found, we extract the optimal policy.
The DQN process is certainly a process requiring an assimilation of all the steps that make up the method, it remains one of the most popular and effective reinforcement learning techniques. You will find it regularly in different variations during your research.
Let see more : https://01codex.com/