SLC S22W1 // Variables y expresiones

Portada diseñada en Canva
1- Explicar dos tipos de variables y expresiones distintos a los que se explican en este curso.
En álgebra, las variables corresponden a símbolos, generalmente son representadas con letras del abecedario, entre las mas comunes son la X y Y. Estas variables, como su nombre lo indica, tienen la particularidad de representar un valor cambiante dentro de una fórmula, ecuación o expresión lógica.
Es decir, que las variables pueden adquirir cualquier valor, y este es determinado debido a una asignación especifica o la resolución de un problema o cualquier tipo de operaciones matemáticas.
Las variables, pueden ser independientes o dependientes.
Variable independiente
Se considera una variable independiente, cuando su valor no depende de ninguna otra variable es decir, que se le pueden asignar valores sin tener en cuenta otras variables. Generalmente, son representadas por la letra (x).
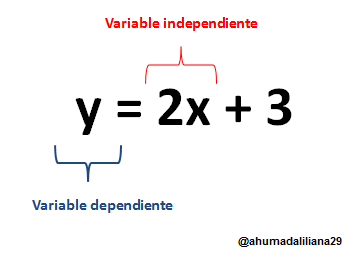
Tipos de Variables - IMG creada en Paint
Variable dependiente
Como su nombre lo indica, en este tipo de variables su valor varia en función de otras variables. Es decir, que el valor de esta, se obtiene del calculo de una ecuación u operación que contenga una o mas variables independiente (x). Generalmente, son representadas por la letra (y).
2- Muestra tu forma de evaluar una expresión algebraica si se dan los valores de las variables. ¡Se requiere una explicación paso a paso!
Gracias a esta lección he aprendido que existe una serie de reglas que nos ayudan a evaluar de forma correcta a las expresiones algebraicas. El PEMDAS es una guía que nos indica el orden en que se deben resolver las operaciones dentro de una expresión matemática.
Puede resultarnos desconocida y un poco complicada esta palabra. PEMDAS es un acrónimo en inglés, es decir, que cada letra corresponde a una palabra y estas nos indican el orden de prioridad para resolver las operaciones matemáticas:
P: Parentheses
E: Exponents
M: Multiplication
D: Division
A: Addition
S: Subtraction
Teniendo en cuenta la siguiente expresión matemáticas, aplicaremos esta guía de prioridades para resolver la operación según el PEMDAS.

Por lo que lo primero que debemos resolver es las operaciones que se encuentren dentro de los paréntesis, en este caso, es una resta. Así que procedemos a restar (4-9), el cual nos arroja el resultado de (-5).

Luego siguen los exponentes, así que procedemos a sacar (-5)², dándonos como resultado 25.

Continuamos resolviendo la multiplicación, que en este caso seria 6x25, dando el como resultado 150.

Continuando con el orden de prioridades de las operaciones, ahora corresponde la división, por lo que dividimos 150÷2, dando como resultado 75.

luego de la división, sigue la suma, así que procedemos a realizar el calculo de 75+5, el cual nos da como resultado 80.

Continuamos, y vemos que en el orden de prioridades para resolver operaciones matemáticas se encuentra la resta, así que procedemos a restar 80-20, así que obtendremos el resultado final que es 60.

Tarea 3
• Simplifica esta expresión: 3(2x - 1) + 2(x + 4) - 5
Teniendo la siguiente expresión, y siguiendo la guía del PEMDAS debemos resolver los paréntesis, así que el primer paso es resolver la multiplicación con los elementos que están dentro del paréntesis que en este caso seria 3.(2x-1) y 2.(x+4)

Continuamos combinando los términos similares para simplificar la ecuación, para ello sumamos 6x+2x.
Y el ultimo paso es resolver la operación matemática que en este caso es realizar la resta de -8+8, por lo que el resultado de la ecuación es 8x.
• Evalúa esta expresión: (x^2 + 2x - 3) / (x + 1) cuando x = 2
En esta expresión se nos indica el valor de nuestra variable independiente, por lo que el primer paso para resolver esta ecuación es sustituir el valor de x.

Luego de haber sustituido el valor de x, procedemos a realizar las operaciones con el orden de prioridad de cada uno, así que en primer lugar resolvemos la potencia de x^2 el cual da como resultado 4.
continuamos resolviendo la multiplicación que se encuentra dentro del paréntesis 2.(2, su resultado es 4.
Finalmente, procedemos a realizar la suma de los términos similares dentro del paréntesis, seguidamente resolvemos la resta y de esta manera obtenemos el resultado de la ecuación que es 5/3.
• Resuelve la siguiente ecuación: 2x + 5 = 3(x - 2) + 1
Para resolver esta ecuación, primero debemos simplificarla lo mas posible, por lo que vamos a eliminar el paréntesis al resolver la multiplicación 3(x - 2).
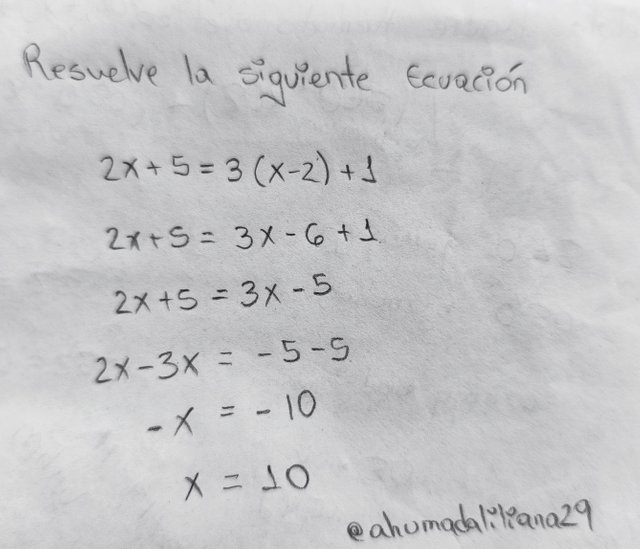
Al tener todos los términos, comenzamos a despejar la x, por lo que vamos a juntar los terminos similares, en este caso vamos a pasar 3x que se encuentra positiva en el lado izquiero, lo vamos a pasar al lado derecho en forma negatia.
y el 5 que esta en el lado izquiero que esta sumando, lo pasaremos al lado derecho restando, por lo que nuestra ecuación quedara de la siguiente manera:
2x-3x = -5+5
Ahora, procedemos a realizar la operación algebraica correspondiente y nos da el siguiente resultado.
-x = -10
Como en ambos lados tanto la variable X y el resultado es negativo, lo que hacemos es dividir en ambos lados entre 1 para anular el negativo de nuestra x.
Tarea 4
• Supongamos que hay una panadería que vende un total de 250 panes al día. Se venden panes de trigo integral y pan blanco, y la cantidad de panes de trigo integral vendidos es 30 veces mayor que la cantidad de panes de pan blanco. Si x representa la cantidad de panes de pan blanco vendidos y la panadería obtiene una ganancia de $0,50 por cada pan blanco y $0,75 por cada pan de trigo integral, escriba una expresión que represente la ganancia diaria total de la panadería.
Según los datos indicados en este ejercicio, podemos ver que necesitamos una variable dependiente para obtener el valor de ganancia total de la panadería.
Y= ganancia total de la panadería.
Luego tenemos una variable independiente que corresponde a la cantidad de pan blanco vendidos.
x=pan blanco vendidos.
y dos constante que corresponden a los precios de los panes:
$0,50 por cada pan blanco
$0,75 por cada pan de trigo integral.
Así que la expresión matemática que represente la ganancia diaria total de la panadería, segun mi entendimiento de esta tarea es la siguiente.
y = 0,50x + (30x . 0,75)
En donde la variable dependiente y, tendrá el valor correspondiente a la multiplicación de 0,50 por x que es la cantidad de pan blanco vendido, a ese resultado se le sumara el calculo de la multiplicación de 30 por x, aquí estaremos obteniendo la cantidad de pan integral vendido, ya que que nos indicio que es 30 veces mayor que la cantidad de pan blanco vendido, a su vez se multiplicara por 0,75 que es el valor de ganancia del pan integral.

• Supongamos que el costo de alquilar un automóvil por un día se representa mediante la expresión 2x + 15 y donde x es el número de horas en las que se alquila el automóvil. Si la empresa de alquiler ofrece un paquete de 3x - 2 dólares para los clientes que alquilan el automóvil durante más de 4 horas, escriba una expresión para el costo total de alquilar el automóvil durante x horas y muestre cómo la simplifica.
En primer lugar, hacemos una evaluación de la información dada en este ejercicio, en el cual se nos muestra que:
** 2x + 15** es la ecuación para representar el calculo de x horas, cuando esta es menor o igual a 4.
Luego tenemos un paquete de promoción para los clientes que alquilan el automóvil durante más de 4 horas
3x - 2
Entonces:
Tenemos dos ecuaciones que se pueden aplicar, según el plan de alquiler que elija el cliente:
CT= 2x + 15 Cuando x ≤ 4.
CT = 3x - 2 Cuando x > 4.
Estas ecuaciones no requieren de simplificarlas, ya que para su aplicación solo se necesita saber cuantas horas el cliente va a alquilar el automóvil y si es mayor a 4 horas se aplicara esta ecuación para calcular el costo total:
CT = 3x - 2
Mientras que si es alquilado el automóvil por 4 o menos horas, la ecuación a aplicar para calcular el costo seria:
CT= 2x + 15
Kindly have a look at some updated tasks at instructions of steemcurator01 and make edits in your post!
Let me know after going through this process so that I may review your post!
0.00 SBD,
0.02 STEEM,
0.02 SP
Disculpe profesor. No sé a cuáles instrucciones se refiere. Si me puede ayudar se lo agradecería, no se que me faltó o que tengo que modificar
0.00 SBD,
0.05 STEEM,
0.05 SP
Please check these updated tasks and edit your posts accordingly!
https://steemit.com/algebra-s22w1/@khursheedanwar/slc-s22w1-variables-and-expressions
I am referring to instructions of steemcurator01 that you can see in comment section of course
Your post is 17 hours ago!
I have to review it,just waiting when you will edit it!
Ya lo edite. Mis disculpas es que estaba cumpliendo con mi jornada laboral y n tenia el tiempo de realizar la modificación.
Ok no worries
I am reviewing it as it is done now!