SLC S22W1//Variables y expresiones

IMG diseñada en CANVA
Tarea 1
Explicar dos tipos de variables y expresiones distintos a los que se explican en este curso. (¡Se requieren ejemplos prácticos y algebraicos!)
Una variable es un símbolo, que usualmente son las letras "x" o "y", estas son utilizadas para representar valores que pueden variar dentro de una fórmula, algoritmo o ecuación.
Basado en sus propiedades matemáticas, las variables pueden ser:
- Variables Cualitativas: estas, como su nombre lo indica, expresan características, cualidades o atributos, es decir, que no pueden ser medidas con números.
Ejemplo:
Variable Sexo esta puede tener dos valores: Femenino o Masculino
Vemos que el valor de esta variable no es numérico, sino que representa una característica o cualidad, que en este caso es el sexo de una persona.
- Variables cuantitativas: son aquellas que se expresan mediante un número, es decir, que representan una magnitud puede ser medida y expresada en términos numéricos y por ende permite realizar operaciones aritméticas con ellas.
Ejemplo:
Variable: Cantidad puede tener cualquier valor numérico.
Variable: Edad puede variar su valor numero, en función de la edad de una persona.
Variable X esta puede tener cualquier valor numérico. X=25
Por otra parte, las expresiones algebraica son la representación de la combinación de diferentes variables, constantes, relacionadas entre si mediante operadores matemáticos (+, - , x , /, etc).
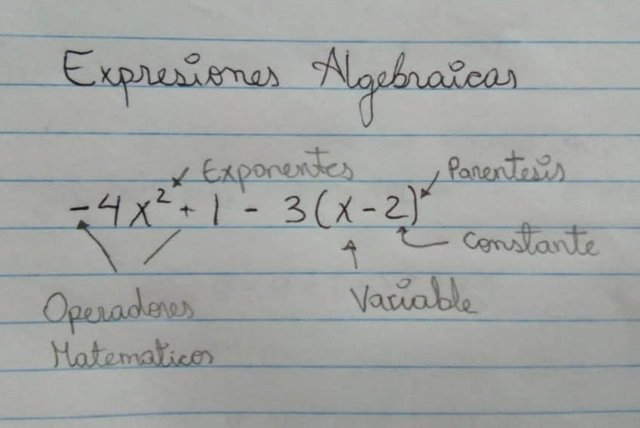
A continuación, les hablare de dos tipos de expresiones matemáticas:
1- Las expresiones radicales: como su nombre lo indica, son aquellas expresiones que incluyen un radical, el cual es el símbolo de calcular una raíz (√).
En esta caso, el radical nos indica que un número debe multiplicarse por sí mismo, la cantidad de veces que otro número se lo indique, para obtener un valor exacto.
Ejemplo:
Por ejemplo, la raíz cuadrada de 16 se expresa de la siguiente manera:
√16 = 4
En este caso, la raíz cuadra de 16 es 4, ya que si multiplicamos 4x4, el resultado es 16.
Otro ejemplo:
3√8
En esta expresión se calcula la raíz cúbica de 8, por lo que se debe hallar el multiplicado por sí mismo 3 veces que dé como resultado lo que está en la expresión numérica que en este caso es 8.
Así si multiplicamos 2x2x2, obtendremos como resultado 8. Así que entonces la raíz cubica de 8 es 2.
3√8=2
2- Expresiones exponencial: este tipo de expresión permite representar multiplicaciones repetidas o potencias en forma abreviada, dentro de esta expresión b es la base y x es el exponente.
El exponente indica la cantidad de veces que se usa la base como factor.
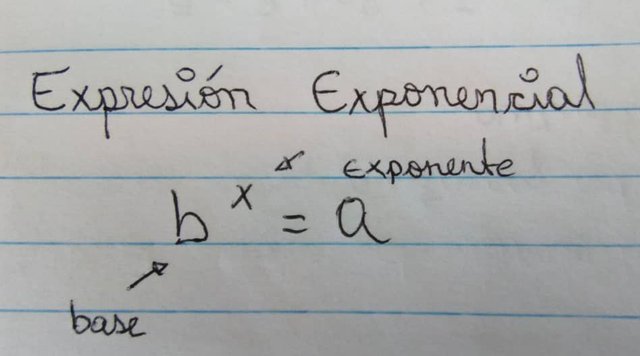
Ejemplo:
Tenemos la multiplicación 10x10, la cual se puede representar exponencialmente como 10². En esta expresión, 10 es la base y 2 es el exponente.
10²
Tarea 2
Muestra tu forma de evaluar una expresión algebraica si se dan los valores de las variables. ¡Se requiere una explicación paso a paso!
Para evaluar una expresión algebraica hay tener muy claro el orden a realizar en las operaciones, ya que de otra forma, podemos obtener un resultado equivocado. Para facilitar esta tarea es necesario entender las Reglas PEMDAS.
Las reglas PEMDAS son los acrónimos que nos indican el orden a realizar las operaciones matemáticas, estas son:
- P: Paréntesis
- E: Exponentes
- M: Multiplicación
- D: División
- A: Suma
- S: resta.
Así que veremos un ejemplo practico para entender su aplicación.
Tenemos la siguiente Expresión: 4x² - 2x + 3 y el valor de X=2
Al conocer el valor de X, lo primero que debemos hacer es sustituir su valor en la ecuacion, por lo que tendríamos:
4(2)² - 2(2) + 3
Ahora procedemos a aplicar las reglas PEMDAS, evaluamos nuestra expresión y consideramos todos sus componentes y vemos que debemos resolver en primer lugares las operaciones que involucren exponentes.
(2)² = 4
Quedando nuestra expresión de la siguiente manera:
4(4) - 2(2) + 3
Seguidamente, debemos resolver las multiplicaciones.
4.4= 8
2.2=4
Quedando nuestra expresión de la siguiente manera:
8 - 4 + 3
Continuamos con la suma, ya que tiene prioridad por encima de la resta
-4+3= -1
Así que la expresión queda:
8-1
Dando como resultado final: 7

Tarea 3
Simplifica esta expresión: 3(2x - 1) + 2(x + 4) - 5
Para simplificar esta expresión, debemos tomar en cuenta las reglas PEMDAS en la cual se nos indica, que el primer paso a realizar es la eliminación de los paréntesis, por lo que debemos realizar las operaciones correspondientes para lograr.
Para lograr esto, aplicaremos la propiedad distributiva, debido a que tenemos la multiplicacion de 3.(2x-1) y 2.(x+4).
Multiplicación:
3.(2x-1) = 6x
2.(x+4)=2x+8

Quedando la ecuación de la siguiente manera:
Paso 2: debemos proceder a agrupar los términos similares, para facilitar la resolución en los siguientes pasos.
Quedando la expresión de la siguiente manera:
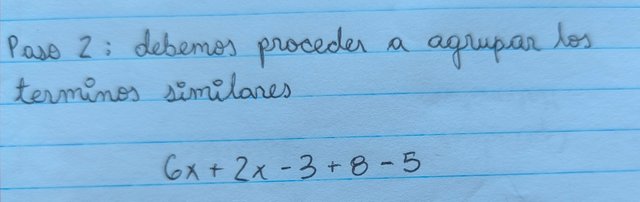
Paso 3: siguiendo la guía de las reglas PEMDAS, en el orden de prioridades debemos resolver primero la suma y luego las restas.
Por lo que vamos a realizar la suma de los términos similares:
6x + 2x= 8X
-3 + 8 = 5 Aplicando la regla de los signos, la cual nos dice que signos diferentes se restan y se mantiene el signo del mayor, por eso restamos -3+8 y el resultado es 5.
Luego nos queda + 5 - 5 en el cual se anulan.

Por lo que nos queda como resultado Final 8X.

Evalúa esta expresión: x² + 2x - 3 / (x + 1) cuando x = 2
El primer paso a cumplir para resolver esta expresión es sustituir el valor de la variable, ya que se nos indica cual es.
Así que al sustituir su valor, la expresión queda de la siguiente manera:
2² + 2(2) - 3 / 2 + 1

Paso 2: aplicando las reglas PEMDAS debemos resolver las operaciones en las cuales estén involucrados los paréntesis para eliminarlos.
2² = 4
2.(2)= 4
Quedando la ecuación de la siguiente manera: 4 + 4 - 3 / 2 + 1

Paso 3: resolvemos las operaciones de suma, ya que tiene prioridad antes que la resta segun las reglas PEMDAS.
4+ 4 = 8
2+1=3
Quedando la ecuación de la siguiente manera: 8 - 3 / 3
Paso 4: para finalizar, debemos resolver la operación de resta.
8-3 = 5
Quedando como resultado 5/3


Resuelve la siguiente ecuación: 2x + 5 = 3(x - 2) + 1
Para resolver esta ecuación, me guiare de las reglas PEMDAS.
Paso 1: eliminar los paréntesis, por lo que aplicare en primer lugar la ley distributiva para realizar dicha multiplicación:
3 (x - 2) = 3X - 6

Quedando nos la ecuación de la siguiente manera: 2x + 5 = 3x - 6 + 1
Paso 2: ahora debemos realizar la agrupación de los términos similares.
Quedándonos de la siguiente forma:
2x - 3x y en este caso, teníamos 3x con signo positivo de lado derecho, al trasladarla al lado izquierdo se coloca con signo negativo.
-5 -6 + 1 y es que el cinco estaba positivo en el lado izquierdo, al trasladarlo al lado derecho se debe cambiar el signo a negativo.
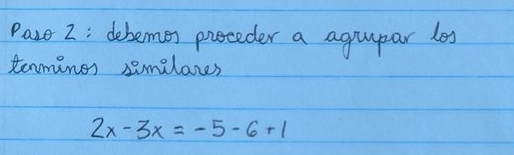
Nuestra ecuación queda de la siguiente manera: 2x - 3x = -5 - 6 + 1
Paso 3: según el orden de prioridades indicado por las reglas PEMDAS, debemos calcular las operaciones de suma.
-6 + 1 = -5 Aplicando la ley de los signos se realiza la resta los numeros y se mantiene el signo del mayor que en este caso nos queda negativo.

La ecuación queda de la siguiente manera: 2x - 3x = -5 - 5
Paso 4: Ahora realizamos las respectivas operaciones de resta.
2x - 3x = -x se realiza la resta y el resultado mantiene el signo negativo.
-5 - 5 = - 10 al ser los dos números negativos, se deben sumar y mantener el signo negativo.

La ecuación queda de la siguiente manera: - x = -10
Paso 5: para finalizar, debemos realizar la multiplicación por 1 en ambos lados, para anular el signo negativo a nuestra variable.

Dando como resultado X=10

Tarea 4
Supongamos que hay una panadería que vende un total de 250 panes al día. Se venden panes de trigo integral y pan blanco, y la cantidad de panes de trigo integral vendidos es 30 veces mayor que la cantidad de panes de pan blanco. Si x representa la cantidad de panes de pan blanco vendidos y la panadería obtiene una ganancia de $0,50 por cada pan blanco y $0,75 por cada pan de trigo integral, escriba una expresión que represente la ganancia diaria total de la panadería.
Para resolver este problema, debemos tomar en cuenta los datos proporcionados.
x corresponde al número de panes blancos vendidos
(x + 30) corresponde a los de panes integrales que se venden. Esta cantidad es determinada de esta manera, ya que nos dice que es 30 veces mayor que la cantidad de panes de pan blanco por eso se establece que es (x+30).
Total de panes vendidos por día = 250.
Para encontrar el valor de X, podemos establecer la siguiente expresión:
x + (x + 30) = 250
Ahora procedemos a simplificar dicha expresión.
2x + 30 = 250 realizamos la suma de términos similares.
2x = 250 - 30 luego trasladamos el 30 el cual estaba sumando, y pasa restando al lado derecho.
x = 220 / 2 Resolvemos la resta y y el 2 que estaba multiplicando a nuestra variable, la pasamos al lado derecho dividiendo.
x = 110 al resolver la división, obtenemos como resultado que el valor de nuestra variable es 110.
Al tener el valor de X, sabemos que los panes blancos vendidos diariamente fueron 110, asi que en base a este resultado podemos calcular la cantidad de pan integral vendido que nos indicaron que es 30 veces mayor, por lo tanto:
Pan integral = 110 + 30 = 140
Ya teniendo esta información, podemos crear una expresión que represente la ganancia diaria total de la panadería, para ello debemos tomar en cuenta la siguiente informacion:
Ganancias
Pan blanco = $0,50
Pan integral = $0,75
Así que la expresión quedaría de la siguiente manera:
Ganancia total = 0,50x + (0,75(x + 30))
Esta expresión aun la podemos simplificar aun mas.
En primer lugar y siguiendo las reglas pendas, debemos eliminar los paréntesis, asi que aplicamos la propiedad distributiva
0,75(x + 30) = 0,75x + 22.5
Quedando la expresión de la siguiente forma:
Ganancia total =0,50x + 0,75x + 22.5
Continuamos haciendo la suma de los términos similares:
Ganancia total =1,25x + 22,5
Ahora bien, sabemos que el valor de x=110, por lo que podemos sustirtuir su valor y calcular el resultado.
Ganancia total =1,25(100) + 22,5
Ganancia total = 137.5 +22.5
Ganancia total =160$
Al vender 250 panes diarios, la panadería obtiene un total de ganancias de 160 $.
Supongamos que el costo de alquilar un automóvil por un día se representa mediante la expresión 2x + 15 y donde x es el número de horas en las que se alquila el automóvil. Si la empresa de alquiler ofrece un paquete de 3x - 2 dólares para los clientes que alquilan el automóvil durante más de 4 horas, escriba una expresión para el costo total de alquilar el automóvil durante x horas y muestre cómo la simplifica.
2x + 15 representa el el costo del alquilar un automóvil.
3x - 2 representa el paquete adicional para los clientes que alquilen durante más de 4 horas.
Con esta información, podemos crear una expresión que nos permita calcular el costo total al alquilar un automóvil durante x horas.
Quedando de la siguiente manera
Costo total = (2x + 15) + (3x - 2)
Podemos simplificar esta ecuación, al agrupar los términos similares.
Costo total = 2x + 3x + 15 - 2
Ahora resolvemos las operaciones de suma y resta, quedándonos de la siguiente manera:
Costo total = 5x + 13
Ya con esta expresión es fácil determinar el costo total del alquiler, solo es necesario tener el valor de x, que seria la cantidad de horas que el cliente desee alquilar el automóvil.
Quiero invitar a @noelisdc, @tahispadron y @mariami para que también participen en este concurso.
Muchas gracias por la invitación.
Está bien interesante el tema del curso.
Saludos y mucho éxito.
Wow amiga muchas gracias por la invitación a este curso , tú sin duda eres una ingeniero nata jajaja, Te felicito porque es notorio que tienes una facilidad matemática para resolver operaciones de esta y también te felicito por tu extraordinaria publicación en la que te deseo el mayor de los éxitos , te lo mereces. Saludos y bendiciones.
Saludos, @khursheedanwar no ha sido verificada mi tarea.
I am verifying
Don't worry