SLC-S22W1/Variables and Expressions

Greetings Steemit friends
Explain any two variables and expression types other than that which are explained in this course. (Practical and algebraic examples are required!)
The variable is a symbol used in a mathematical equation, which is a placeholder to represent an unknown or changeable value. At the same time, an expression combines variables, numbers, and operations in a mathematical equation.
In the course, we mentioned the Independent variable and dependent variable. So I will go ahead to look at other types like Continuous and Discrete Variables.
Continuous Variables: This is a variable that can have any value within a given range without placing any restriction on whole numbers or fractions. Continuous can hold float values, mostly in measurements like temperature, weight, time, etc.
A practical example will be the temperature variable to get the weather forecast, as a given range of °C is being used. That is why we can have different temperatures, for example, 20.5°C, 20.55°C, 20.58°C, etc.
T is the temperature of an area in °C, and the temperature changes (rise) at a rate of 0.5°C per hour.
T=20+0.5t
t represents the time (in hours) of the temperature at any time. So now in our equation, we have to continue variables. That is T(Temperature) and t (time).
Discrete Variables: This is different from continuous variables, as here values are distinct and typically whole numbers. Discrete are countable and do not have cases of fractions. Examples of the number of people in a hall, and the number of books in a bookstore. Etc.
A practical example is several cars in a parking lot for sale. We can sell a fractional car LOL, only a whole car can be sold out. We can see a clear expression of a discrete variable.
x represents the number of cars, and each car costs FCFA 2 500 000. The cost of the car represents C for us to have our expression.
C = 2 500 000x
That means if we buy two cars.
C = 2 500 000(2)
C = 5 000 000
C is a whole number because x was a discrete variable.
In the course, we mentioned the Numerical expressions and Algebraic expressions. So I will go ahead to look at other types like Polynomial and Rational Expressions.
Polynomial Expressions: This is an algebraic expression making sum operations of different terms with a variable raised to a non-negative integer power. Polynomial Expressions have constant terms and do not have any denominator with variables,
Practical example,
C=3^2 + 2 + 5x + 50We have x with the squared team
We have the 5x which is the linear team
We have 50, which is the constant
Rational Expressions: This is the algebraic expression in a fraction form with both the numerator and denominator having a variable and polynomials. In this case, the denominator cannot be zero. In other words, rational expression can be seen as dividing a polynomial by a polynomial.
Practical example,
10x/x +210xis the numerator rational expressionx + 2is the denominator rational expression.
Show your way of evaluating an algebraic expression if values of variables are given. Step-by-step explanation required!(The more you will be detailed and accurate, the more your task will be perfect!)
Here we have to start by getting our algebraic expression, and then getting the given values for the variable. After replacing the value in place of the variable, we can go ahead to follow the order of operations (PEMDAS)
Let's make use of Polynomial Expressions.
2x^2 +3y−4z Values: x=3, y=2, z = 3
Step 1: Replace the variables (x, y, and z) with the values (3,2, and 3) respectively.
2(3)^2 +3(2)−4(3)
Step 2: Start with the exponents
Now we have
2(9) + 3(2) - 4(3)
Step 3: Let multiply, to take off the brackets
2(9) = 2x 9 = 18
2(3) = 2x3 = 6
4(3) = 4x3 = 12
Our expression now becomes
18 + 6-12
Step 4: We now have a simpler expression to go ahead with to make use of additions and subtraction.
Start with addition, 18 + 6 = 24
Next, we subtract 24 - 12 = 12
So our final result is 12
Task 3
• Simplify this expression: 3(2x - 1) + 2(x + 4) - 5
• Evaluate this expression: (x^2 + 2x - 3) / (x + 1) when x = 2
• Solve the following equation: 2x + 5 = 3(x - 2) + 1
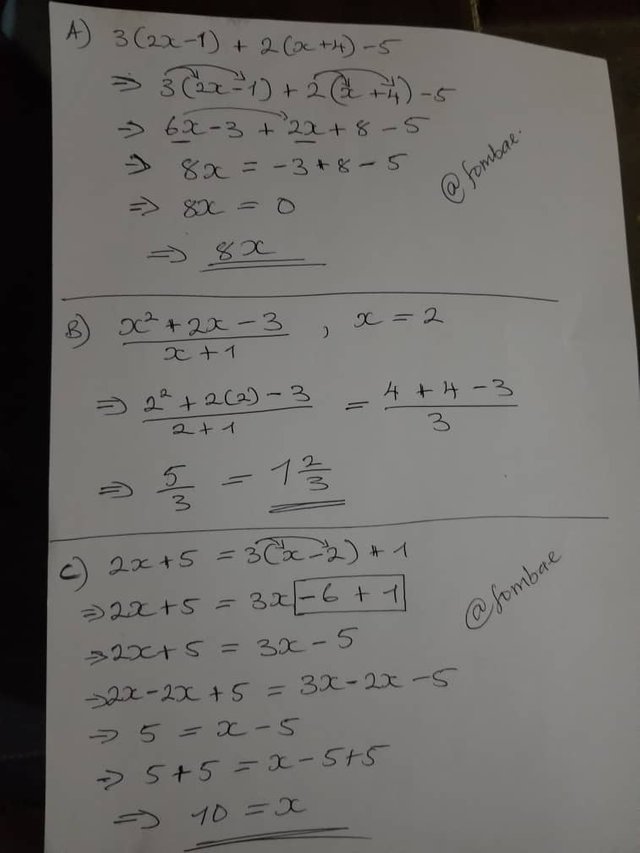
Task 4
Let's start by breaking down information in the first scenario.
- The total sales per day is
250( that is both white and whole wheat bread loaves). - We have
30more whole wheat than white loaves xrepresents white bread$0.50profit for each white bread$0.75profit for each whole wheat
I will start by subtracting the th 30 from the 250
250 - 30 = 220. Both white and whole wheat bread loaves will be equal at this point.
2x = 220
So our expression will look like this.
x + (x+30) = 250That is
white bread + whole wheat = 250 .
From here, I think it is pretty simple to get the exact value of x and the number of white and whole wheat loaves.
x + (x+30) = 250
2x + 30 = 250
2x = 250-30
2x = 220
x = 220/2
x = 110
White bread = 110
Whole wheat = 110 +30 = 140
We have the extracted amount of loaves for both white and whole wheat and can go ahead now to get our profit for each category.
White bread loaves : 0.50 x 110 = 55
Whole wheat loaves : 0.75 x 140 = 105
Total profit for the sell per day (250 loaves): 55 + 105 = $160
=================================
Let's start by breaking down information from the second scenario.
- Cost of renting a car =
2x + 15 - Note that
xis the number of hours.
Now the company has gone ahead to give a special package for customers who exceed 4 hours.
So if x(number of hours) is more than 4, the cost will be calculated 3x-2
Here we have two expressions, which have been simplified already.
Case 1 : x ≤ 4, 2x + 15
Case 2 : x > 4, 3x -2
So here, any of the expressions can only be used depending on the value of x. that is less than 4 for case 1 and greater than 4 for case 2.
Cheers
Thanks for dropping by
@fombae