---

As-salamu Alaykum ( 'Peace be upon you')

---

I am pleased to participate in the 1st of SLC Season 22. This week we will be learning Variables and Expressions. Mathematics was my favourite subject, and I was quite good at this, but when I was in class 11th, I fell in love with Biology (haha), so I broke up with mathematics. I hope this course will remind me of my school days. Thanks to @khursheedanwar for creating this opportunity to show our skills and learn about mathematics. So Let's start,

^{Made with Canva}

---

Explain any two variables and expression types other than that which are explained in this course. (Practical and algebraic examples are required!)

---

A variable is a symbol or letter that represents an unknown value. It may have only one value or it may change over time or as needed for a mathematical problem. In a word, a variable doesn’t have a fixed value. (It is often the letter X.). They act as symbols that represent unknown values. On the other hand, expressions are numbers, symbols or operators (such as addition, subtraction, multiplication and division) and they act as mathematical phrases to show the relationship between numbers and variables. For example, the expression “3X +5” means “trice the value of X plus five.” From this course lecture, we come to know about

• Independent variable - As per Its name, it doesn't depend on another variable.
• Dependent variable - As per Its name, it depends on another variable. Below, I am explaining two variables and expression types other than those that are explained in this course.

---

Binary Variable

---

This is a variable that can take only two possible values. That is, 0 and 1 or it can be said to be true or false, yes or no. A practical example of this is whether a student participated in an exam or not (1 for participation, 0 for non-participation).
To explain this with an algebraic example,
x= represents the state of participation.
If 𝑥=1, he participated and if
𝑥=0, he did not participate.

---

Categorical Variable

---

As per Its name, it is a variable that represents only categories or groups. It doesn’t take any numbers. For a practical example, we can say the types of fruits like apples, bananas, and oranges. For an Algebraic Example- Suppose X represent fruit types and x=1 for apple, x=2 for banana, and x=3 for orange.

---

Inequality Expression

---

An inequality expression is a mathematical statement that compares two or more expressions. It shows the relationship where two sides are not the same or equal, using symbols like >, <, ≥,≤.
For a practical example, a student has to get at least 50 marks to pass. The Algebraic Example is X≥50. Here X is the student's number.

---

Exponential Expression

---

Exponential expression is a way to write powers in short form. The exponent indicates the number of times the base is used as a factor. So we can explain it like 32 it can also be written as 2 × 2 × 2 × 2 × 2=32, where 2 is the “base”, and 5 is the “exponent”. We read this expression as “two to the power five”.

---

Show your way of evaluating of an algebraic expression if values of variables are given? Step-by-step explanation required! (The more you will be detailed and accurate, the more your task will be perfect!)

---

To evaluate an algebraic expression, we mainly substitute the values there provided for the variables and calculate using the exact sequence of operations (PEMDAS). From the lecture, we learnt what is PEMDAS

• P stands for parentheses, which are useful for the evaluation of expressions in parentheses in the first order.
• E stands for exponents, which are used for evaluation of any exponential expressions as second-order like 2^3.
• M stands for multiplication in third order.
• D stands for division in fourth order.
• A stands for addition as fifth order.
• S stands for subtraction as the sixth order.

Example 1: 3x+2y [Given Values: x=4, y=5]

---

Step 1: Write the expression

---

3x + 2y

---

Step 2: Substitute the values of variables

---

Replace x with 4 and y with 5 as the given value.

3(4)+2(5)

---

Step 3: Perform the multiplication first

---

12+10

---

Step 4: Perform the addition

---

12+10=22

---

Final Answer: The value of the expression is 22.

---

Example 2: 2x²−4y + z [Given Values: x=3, y= 2, z = 1]

---

---

Step 1: Write the expression

---

2x²−4y + z

---

Step 2: Substitute the values of variables

Replace x with 3, y with 2, and z with 1

2(3^2) − 4(2)+1

---

Step 3: Simplify exponents

---

2(9)−4(2) + 1

---

Step 4: Perform multiplication

---

18 - 8 + 1

---

Step 5: Perform addition and subtraction in order

---

18−8= 10
10+1=11

---

Final Answer: The value of the expression is 11.

Example 3:

---

I will show this Example on paper following the previous process.

---

Simplify this expression: 3(2x - 1) + 2(x + 4) - 5 and Evaluate this expression: (x^2 + 2x - 3) / (x + 1) when x = 2 and Solve the following equation: 2x + 5 = 3(x - 2) + 1

---

^Senerio-1

Initially I start writing the expression which is

3(2x - 1) + 2(x + 4) - 5

Here I applyed BODMAS rules. So here are the steps

---

Step 1: Distributing in the first term

---

3(2x-1)
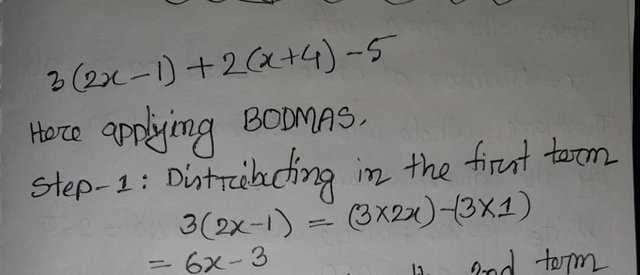
= (32x)-(31)
= 6x-3

---

Step 2: Distributing in the second term- In this step I got 2x+ 8
Step 3: Distributing in the second term- Combine them all and my final answer is 8x.

---

Problem-2

---

^Senerio-2

Write the expression then put the value of X. As per BODMAS and my final answer is 3/5.

I got the Denominator is 3 and the numerator is 5.

---

Problem- 3

---

^Senerio-3

---

First I write the expression then work on right hand side and left hand side. Then rearrange the equation.
2x+5=3x-6+1
Or, 2x-3x=-6-5+1
Or, -x=-10
Then divided bith sides by -1.
So, X=10.
Final answer is 10.

---

task-4

---

Suppose there's a bakery selling a total of 250 loaves of bread per day. They are selling whole wheat and white bread loaves with numbers of whole wheat loaves sold being 30 more than the number of white bread loaves. If x is representing number of white bread loaves sold out and bakery is making a profit of $0.50 for each white bread loaf and $0.75 for each whole wheat loaf then please write an expression for representing bakery total daily profit.

From the given info,

• The number of white loaves sold =X
• The numbers of whole wheat loaves sold being 30 more than the number of white bread loaves
  So, Whole wheat loaves= x+30

As per the condition,

White loaves+whole wheat loaves =250
X+X+30=250
2X+30=250
2x=250-30
2X=220
X=110

So, the number of white loaves is 110.

---

Now we know the number of white loaves and from that we can get number of whole wheat loaves.

X+30= Wheat loaves number
110+30=140

---

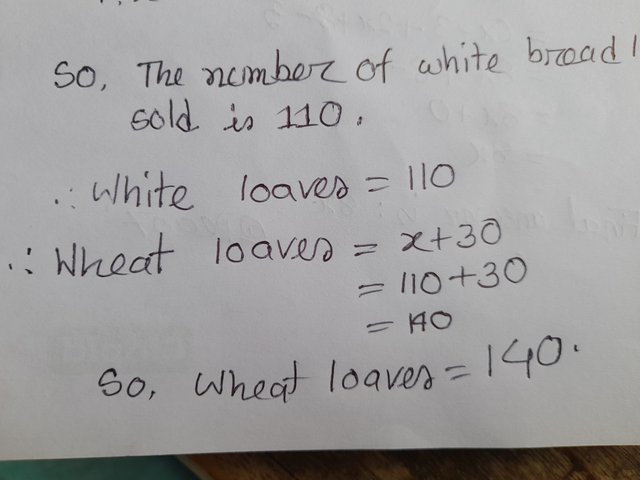
Again, From the question we can get the total daily profit expression

Total profit= profut of white loaves+ profit of whole wheat loaves
Total profit= 0.50*x+0.75(x+30)
Total profit= 0.5x+ 0.75x+22.5

So the final expression for daily total profit is =1.35x+22.5
=(1.35*110)+22.5
= 137.5+22.5
=160 dollar(Ans)

Suppose that cost of renting a car for a day is re-presented by the expression 2x + 15 and here x is the number of hours in which car is rented. If the rental company offers a package of 3x - 2 dollars for customers who take car at rent for more than 4 hours then write an expression for the total cost of renting the car for x hours and show how you simplify it.

---

To write an expression for the total cost of renting a car for x hours, I first analyzed the available data. The cost of renting a car for one day is given by the expression 2x + 15. Here x represents the number of hours. If the rental period is more than 4 hours, the rental company offers a package of 3x - 2 dollars.

So here are two fields,

Rental Cost for 4 Hours or Less (x ≤ 4)
In this case the expression is 2x+15.

Rental Cost for More than 4 Hours (x > 4)

---

In this case, the package expression 3x - 2 is used instead of the base cost 2x + 15, so the general expression for the total cost is:

Total Cost = (2x + 15) + (3x - 2)

To simplify the expression, I sremove bracket (BODMAS) rule
= 2x + 15 + 3x - 2
= 2x+3x+15-2 ( x are grouped together and the constant terms are grouped separately)
=5x+13(combined x and substract 2)
So the simplified cost for the total is 5x+13.

---

I am inviting my friends @impersonal,
@sohanurrahman @mayberling to participate

Thanks everyone for reading my post

Regards

@pea07