SLC-S22W2/Equations and inequalities
 Fuente
Fuente 
Ecuaciones lineales.
Las ecuaciones lineales se pueden diferenciar de las ecuaciones cuadráticas en los siguientes aspectos:
-
Forma general.
La forma que caracteriza una ecuación lineal general es:
a1x1+a2x2+...+anxn
donde x1, x2,…, xn son las variables o incógnitas y a1, a2,…, an son las constantes o coeficientes que suelen ser números reales.
Una de las formas más comunes y simples de este tipo de ecuación es y = mx + n donde “y, x” son las variables, “m, n” son las constantes.
Ejemplo:
y = 2x+1, donde “y” es la variable dependiente, “x” la variable independiente, 2 y 1 son las constantes.
Las variables solamente se involucran con sumas y restas entre sí. No pueden multiplicarse, tener exponentes mayores a 1, ni estar dentro de radicales, logaritmos etc.
Ejemplo práctico:
Juan duplica el dinero de Carlos. Entre ambos reúnen 3000 monedas. ¿Cuántas monedas tiene cada uno?
j = son las monedas de Juan
x =son las monedas de Carlos
m =son el total de monedas
Por tanto, se debe cumplir que
m = j+x =3000
- sustituimos j = 2x y obtenemos (2x + x) = 3000
- sumamos (2x+x)=3x y obtenemos 3x = 3000
- despejamos x dividiendo por 3 y obtenemos x = 1000
- sustituimos en j = 2x tenemos j = (2)1000 y obtenemos j = 2000
-
Grado.
El grado es el máximo exponente de una variable dentro de una ecuación. La ecuación lineal se caracteriza por ser de grado 1, ya que es el máximo exponente que posee la variable es igual a 1. -
Soluciones.
Las ecuaciones lineales tienen infinitas variables o incógnitas como se puede observar en la forma general, por tanto pueden tener una, dos, tres,... infinitas soluciones.
Ejemplo:
x+1 = 0 (tiene una variable “x” y una solución: x = -1) x+y = 0 (tiene dos variables “x,y” infinitas soluciones: x = y), para cualquier valor de “y” existe un valor de “x” idéntico).
-
Representación gráfica.
Las ecuaciones lineales como su nombre lo indica representan gráficamente líneas rectas. Si consideramos una de las formas más comunes como y = mx + n y la representamos gráficamente en un plano cartesiano “x,y”, obtenemos una línea recta con pendiente “m” y corte en la ordenada “n”
Ejemplo:
y= 2x - 1
Para x=0, y=-1 y cuando x=0.50, y=0. Por tanto, esta recta se puede graficar con dos puntos cartesianos (0;1) y (0.50;0), como se muestra a continuación:
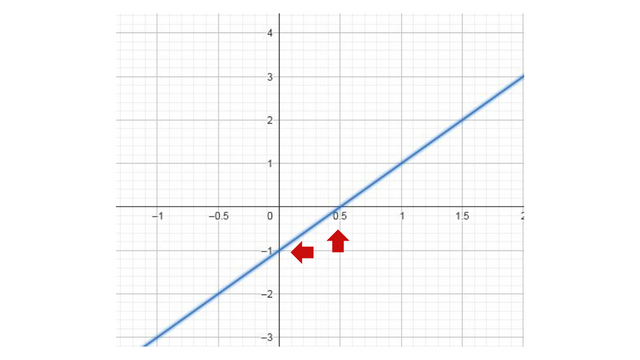 Gráfica de ecuación lineal y=2x-1 / Fuente
Gráfica de ecuación lineal y=2x-1 / Fuente
La ecuación y=2x-1 me indica que la pendiente de la recta m =2 y el corte en la ordenada n = -1. Se puede comprobar gráficamente que el corte en la ordenada pasa por el valor -1 y que la pendiente corresponde a (1/0.50) = 2
Ecuaciones cuadráticas.
Las ecuaciones cuadráticas se pueden diferenciar de las ecuaciones lineales en los siguientes aspectos:
-
Forma general.
La forma que caracteriza una ecuación cuadrática es:
ax2+bx + c
donde x es la variable o incógnita y a,b,c son las constantes o coeficientes que suelen ser números reales. Por lo general se muestra igualada a cero.
Son ecuaciones muy importantes que han facilitado la resolución de problemas reales.
Ejemplo:
x2-4x +3 = 0
Resolviendo esta ecuación por factorización tenemos que:
x2-4x +3 = (x-1)(x-3) =0
Por tanto las soluciones de la ecuación son x=1 y x=3
Ejemplo práctico:
Una pelota se deja caer de una torre y tarda en caer 5 segundos. Determina la altura de la torre.
Cuando se deja caer libremente un cuerpo desde una altura se cumple la ecuación cuadrática de Isaac Newton
h = Vt-½ gt2+H
Donde,
h es la altura en metros al final del movimiento
V es la velocidad inicial del cuerpo en m/seg
t es el tiempo en seg desde que inicia el movimiento
g es la aceleración de gravedad = 9.80 m/seg2
H es la altura a la que se deja caer el cuerpo
Definimos que h = 0 pues el cuerpo al final cae en el suelo, V = 0 porque el cuerpo parte de reposo. Entonces simplificamos la expresión como sigue:
0 = -½ gt2+H procedemos a despejar H de la expresión
H = ½ gt2 donde sustituimos los valores de g y t conocidos
H = ½(9.80)(5)2 luego se resuelve la multiplicación
H = 122.50
Respuesta: La altura de la torre (H) es 122.50 metros
-
Grado.
La ecuación cuadrática se caracteriza por ser de grado 2, ya que es el máximo exponente que posee la variable es igual a 2. -
Soluciones.
Las ecuaciones cuadráticas tienen dos soluciones denominadas raíces, no necesariamente distintas. Éstas pueden ser números reales o complejos.
Las dos soluciones para una ecuación de la forma ax2+bx+c =0 pueden calcularse por la siguiente fórmula general:
x1 = [-b + (b2-4ac)½]/(2a)
x2 = [-b - (b2-4ac)½]/(2a)
-
Representación gráfica.
Las ecuaciones cuadráticas representan gráficamente curvas parabólicas. Si graficamos en un plano cartesiano la ecuación resuelta anteriormente y = x2-4x +3 tenemos que sus dos raíces 1 y 3, definen dos puntos en las abscisas (1;0) y (3;0).
También se puede definir el punto donde la pendiente es cero por la siguiente relación general: 2ax+b =0. Aplicando a la ecuación que queremos graficar tenemos: 2(1)(x)-4 =0, lo que resulta x = 2.
Por tanto, cuando x=2 la ecuación y = (2)2-4(2)+3 = 4-8+3 = -1. Es decir, el punto donde la pendiente es cero es (2;-1) y se encuentra ubicada debajo de las raíces por lo cual es una parábola convexa que tiene dicho punto como el más bajo de la curva.
Otro punto que podemos evaluar en la ecuación es el corte en la ordenada cuando x=0 tenemos y= (0)2-4(0)+3 =3. Es decir en el punto cartesiano (0;3)
En resumen tenemos los siguientes puntos cartesianos típicos con los cuales podemos graficar la parábola y = x2-4x +3.
Puntos (x;y): (1;0), (3;0), (2;-1), (0;3) como se muestran en el gráfico
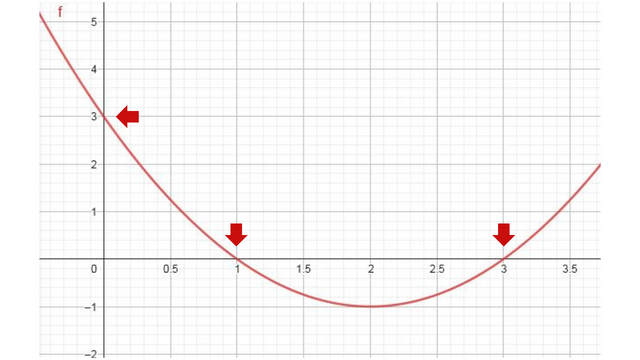 Gráfica de ecuación lineal y=x2-4x+3 Fuente
Gráfica de ecuación lineal y=x2-4x+3 Fuente

Existen diferentes tipos de inecuaciones o desigualdades que dependen de distintas operaciones y relaciones. Entre ellas tenemos:
- Lineales
- Cuadráticas
- Racionales
- Polinómicas
- Valor absoluto
- Exponencial
Son las inecuaciones que contienen fracciones algebraicas. Estas se pueden resolver siguiendo los siguientes pasos:
- Poner las fracciones algebraicas a un lado de la inecuación de manera que el otro lado quede en cero.
- Determinar los valores que anulan el numerador y el denominador.
- Los valores que anulan el denominador no forman parte de la solución.
- Representar en un diagrama de signos los puntos críticos anteriores.
- De lo anterior determinar los intervalos que cumplen con la inecuación.
Ejemplo 1.
(x+8)/(x-1) >1Paso 1. Poner las fracciones a un lado de la expresión y transformar la inecuación
- Restamos 1 en cada lado de la expresión y tenemos: (x+8)/(x-1)-1>0
- Multiplicamos ambos lados por (x-1) y tenemos: (x+8-x-1)/(x-1)>0
- Simplificamos la suma del numerado y tenemos la transformación: (2x+7)/(x-1)>0
Paso 2. Determinar los valores que anulan el numerador y el denominador
Anulación del numerador.
- Igualamos a cero el numerador y tenemos: (2x+7) =0
- Sumamos 7 en ambos lados y tenemos: (2x = -7)
- Dividimos por 2 ambos lados y tenemos el valor que anula el numerador: x = -7/2
- Igualamos a cero el numerador y tenemos: (x-1) =0
- Sumamos 1 en ambos lados y tenemos el valor que anula el denominador: (x =1)
Paso 4. Diagrama de signos con los puntos críticos. Los signos de la fracción en los diferentes intervalos los observamos en el siguiente diagrama:
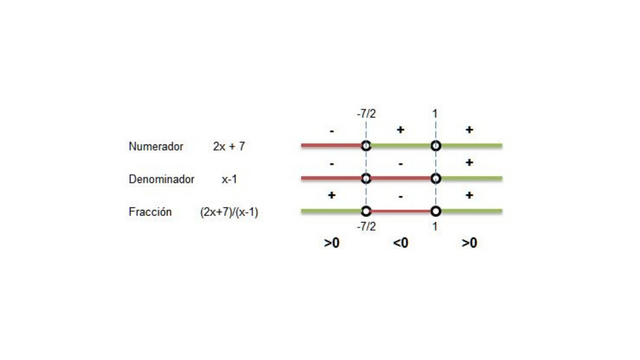 Diagrama de signos con los puntos críticos.
Diagrama de signos con los puntos críticos.
La solución a la inecuación racional es el intervalo donde la combinación de signo satisface la inecuación. En este caso, corresponde al intervalo donde la fracción sea de signo positivo (+) o mayor a cero como resultado de dividir los signos del numerador y denominador. El intervalo intermedio no satisface la inecuación.
Paso 5. Determinar los intervalos que cumplen con la inecuación. La solución de la inecuación racional planteada se encuentra en los dos intervalos siguientes:
x>1 ó x < -7/2
Por tanto, la solución está en: -7/2>x>1
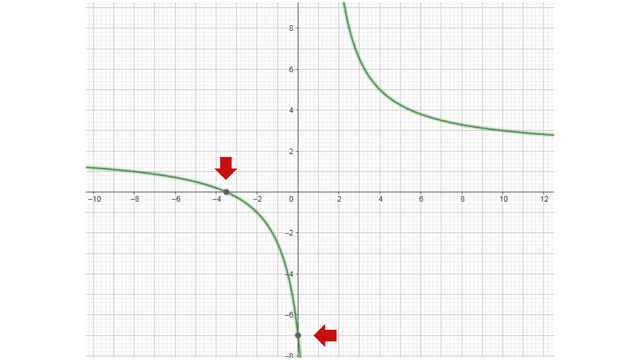 Grafica de la inecuación (2x+7)/(x-1) Fuente
Grafica de la inecuación (2x+7)/(x-1) Fuente
Gráficamente se identifican dos curvas una de las cuales es asíntota y no representa la solución. En la otra gráfica se observan los puntos críticos que cortan los ejes.
Inecuaciones con valor absoluto
Una inecuación de valor absoluto es una inecuación lineal combinada con el concepto de valor absoluto. La variable se encuentra dentro de un operador de valor absoluto.
El valor absoluto de un número x está representado por |x|, por tanto su valor siempre se representa con signo positivo. Por ejemplo:
|-x| = x
|-2| = 2
|2| =2
|0| = 0
Si tenemos una inecuación |x| < b, ésta se puede expresar como –b<x<b. Ejemplo práctico:
|3x-5|< 3-x
- Escribimos la inecuación como -(3-x)<3x-5<3-x
- Simplificamos el lado izquierdo y tenemos: x-3<3x-5<3-x
- Resolvemos la inecuación del lado izquierdo: x-3<3x-5
- Pasamos la x de la izquierda al otro lado y tenemos: -3<3x-x-5
- Sumamos 3 en ambos lados, sumamos términos y tenemos: 0<2x-2
- Dividimos por 2 en ambos lados y tenemos: 1<x
- Resolvemos la inecuación del lado derecho: 3x-5<3-x
- Pasamos la x de la izquierda al otro lado y tenemos: 4x-5<3
- Sumamos 5 en ambos lados, sumamos términos y tenemos: 4x<8
- Dividimos por 4 en ambos lados y tenemos: x<2

Resolución de la ecuación 2x+5 = 11
Paso 1. Para despejar la variable x de la ecuación comenzamos por anular la constante 5 restando su valor en ambos lados de la igualdad como sigue:
2x+5-5 = 11-5
2x = 11-5
Paso 2. Resolvemos la sustracción (11-5) en el lado derecho:
2x = 6
Paso 3. Seguidamente simplificamos la ecuación dividiendo ambos lados por 2, de tal manera que la variable quede despejada:
(2/2)x = (6/2)
x = 3. (Respuesta)
Ejemplo práctico
Frank tiene un total 11 regalos para repartir entre sus 2 amigas y 5 hermanos. ¿Cuántos regalos recibiría cada una de sus amigas si entrega uno a cada hermano?Se dice que 2 amigas reciben x regalos y que los 5 hermanos reciben uno cada uno. Entonces se debe cumplir que los regalos de las amigas y hermanos totalizan 11. En este caso, la totalidad de los regalos se puede expresar algebraicamente como:
2x + 5 = 11
Donde 2son las amigas, x es la cantidad de regalos para cada amiga, 5es la cantidad de regalos a los hermanos y 11es el total de regalos. Por tanto, x = 3 como se demuestra en la resolución previa de la ecuación, lo cual podemos comprobar sustituyendo el valor de x en dicha ecuación como sigue:
(2)(3)+5 = 11
(6+5) = 11
11 = 11 ¡Comprobado!


Escenario: La panadería de Tom
La panadería de Tom es una de las panaderías más famosas de remolque y es famosa por sus deliciosos pasteles y panes. Tom, el propietario, quiere asegurarse de que tiene suficientes ingredientes para preparar su famosa tarta de chocolate y la receta de la tarta de chocolate necesita 2 tazas de harina, 1 taza de azúcar y 1/2 taza de cacao en polvo para cada tarta.
| Ecuación | Si Tom quiere hacer x pasteles y tiene 10 tazas de harina, 8 tazas de azúcar y 4 tazas de cacao en polvo, calcule el número de tartas que puede hacer. |
Simplifiquemos la relación de los ingredientes de una tarta como sigue en la siguiente ecuación:
x= 2h +1a +c/2
Donde,
x es una tarta
h es una taza de harina
a es una taza de azúcar
c es una taza de cacao
Veamos cuántos pasteles se pueden hacer con cada ingrediente individual:
Con 10 tazas de harina se hacen (10h/2h)x = 5x
Con 8 tazas de azúcar se hacen (8a/1a)x = 8x
Con 4 tazas de cacao se hacen (4c/(½c))x = 8x
Por tanto, cuando se alcance la 5ta. tarta se agotará la harina disponible y Tom no podrá hacer más tartas con los tres ingredientes básicos.
Para 5 tartas multiplicamos por 5 ambos lados de la ecuación: x= 2h+a+c/2 como sigue:
5x = (2)(5)h+(5)a+(5/2)c
5x = 10h+5a+(5/2)c
Por tanto, para hacer 5 tartas se requieren 10 tazas de harina, 5 tazas de azúcar y 2½ taza de cacao.
En tal sentido, podemos asegurar que Tom tiene suficiente cantidad de estos ingredientes para hacer 5 tartas.
La respuesta es 5 tartas.
| Inecuación | Tom quiere asegurarse de que dispone de azúcar suficiente para cubrir las necesidades de su tarta de chocolate. También sabe que cada tarta necesita 1 taza de azúcar y que dispone de 8 tazas de azúcar. También sabe que quiere hacer al menos 6 tartas. |
Si x es la cantidad de tartas de chocolate, en este caso, Tom dispone de un máximo de 8 tazas de azúcar, es decir que x ≤ 8 Por otro lado, si Tom quiere hacer al menos 6 tartas requiere al menos 6 tazas de azúcar a razón de una taza por tarta. Es decir que x ≥ 6
Estas dos condiciones se simplifican en la siguiente inecuación:
6 ≤ x ≤ 8Por tanto, Tom dispone de azúcar suficiente para realizar las 8 tazas de azúcar disponibles son suficientes para cubrir las necesidades de la tarta de chocolate ya que dicha cantidad cumple con la inecuación.
Escenario: Número de galones que Ashley necesita
Supongamos que hay una persona llamada Ashley que está planeando un viaje por carretera desde la ciudad A a la ciudad B. Si hablamos de la distancia entre dos ciudades, entonces es de alrededor de 240 millas. El tanque del coche de Ashley tiene capacidad para 12 galones de gasolina. Supongamos que su coche recorre 20 millas por cada galón, entonces ¿cuántos galones de gasolina puede comprar Ashley si ya tiene 2 galones en su tanque y quiere que le sobre al menos 1 galón cuando llegue a la Ciudad B?
| Ecuación | Consideremos x como el número de galones de gasolina que Ashley puede comprar. |
Consumo de gasolina del viaje. Se determina dividiendo la distancia a recorrer por el rendimiento del galón, es decir (240/20) = 12 galones.
Reserva final del tanque. La capacidad máxima del tanque es de 12 galones, por tanto, se consumirán por completo al final del viaje. En tal sentido, Ashley necesitará surtir de nuevo, antes de completar el recorrido, al menos un galón que servirá de reserva.
En resumen se debe cumplir la siguiente relación:
Total de gasolina = Consumo del viaje + Reserva final del tanque
Por tanto se puede expresar en la siguiente ecuación:
(x+2)=(240/20)+1 donde x es la cantidad de galones a comprar
- A la derecha dividir (240/20)=12 y tenemos: (x+2)=(12+1)
- A la derecha sumar (12+1)=13 y tenemos: (x+2)=13
- A la derecha restar 2 en ambos lados y tenemos: x = (13-2)
- A la derecha restar (13-2) y tenemos: x=11 x=11
| Inecuación | x+2 ≥ (240/20)-1 |
Debo aclarar que esta inecuación tiene un error en su planteamiento por lo que su resolución no dará el resultado correcto al problema. Sin embargo, la resolveré tal como me la piden para cumplir con lo solicitado, haciendo la salvedad del resultado.
Resolvemos la inecuación como sigue:
- A la derecha dividir (240/20)=12 y tenemos:(x+2) ≥ (12-1)
- A la derecha sumar (12-1)=11 y tenemos: (x+2) ≥ 11
- A la derecha restar 2 en ambos lados y tenemos: x ≥ (11-2)
- A la derecha restar (11-2) y tenemos: x ≥ 9
x ≥ 9

Respuesta. Si Ashley compra al menos 9 galones adicionales a los 2 que tiene en tanque tendrá al menos 11 galones para iniciar el viaje. Sin embargo, éstos serán insuficientes ya que su coche consume 12 galones para hacer el viaje por tanto, no podrá llegar a su destino y mucho menos tener 1 galón de reserva. En definitiva, la inecuación solicitada no resuelve el problema de Ashley.
A continuación indico la inecuación correcta al problema basado en la ecuación resuelta al principio de esta tarea:
Resolvemos la inecuación planteada como sigue:
- A la derecha dividir (240/20)=12 y tenemos: (x+2) ≥ (12+1)
- A la derecha sumar (12+1)=13 y tenemos: (x+2) ≥ 13
- A la derecha restar 2 en ambos lados y tenemos: x ≥ (13-2)
- A la derecha restar (13-2) y tenemos: x ≥ 11
x ≥ 11

Respuesta. Si Ashley compra al menos 11 galones adicionales a los 2 que tiene en tanque, tendrá al menos 13 galones para hacer el viaje, si su coche consume 12 galones en el viaje le sobrará al menos 1 galón que es la reserva mínima que quiere Ashley al llegar a su destino. Por tanto, la compra de al menos 11 galones es la respuesta correcta.
Saludos @khursheedanwar

Notas:
📌 Imágenes presentadas con la aplicación canva.com
📌 Invito a participar a mis amigos @ridwant @patjewell @paholags @marito74 @genomil @cruzamilcar63 @dasudi @dove11 @goodybest
📌 Más información del concurso en el siguiente enlace.
📌 Mi twitter: steemit_casv
📌 Invito a participar a mis amigos @ridwant @patjewell @paholags @marito74 @genomil @cruzamilcar63 @dasudi @dove11 @goodybest
📌 Más información del concurso en el siguiente enlace.
📌 Mi twitter: steemit_casv
¡Gracias por su visita!

@tipu curate
;) Holisss...
--
This is a manual curation from the @tipU Curation Project.
Upvoted 👌 (Mana: 4/6) Get profit votes with @tipU :)
Post promocionado en X.com
https://x.com/steemit_casv/status/1873524573603598513
Saludos
Hola amigo, estás en tu elemento vale ja, ja, ja, te deseo éxitos en el desafío, un gran saludo desde Margarita y mis mejores deseos para ti y tu familia en el 2025. La matemática siempre está presente en nuestra vida, en mi época liceista la odiaba ja,ja,ja, creo se debió también a los profesores en ese momento pero con el tiempo aprendí a valorarla.
Con dos hijos liceistas he tenido que volver a repasar muchos aspectos entre ellos las ecuaciones, a dios gracias ellos son muy prácticos y han salido adelante sin problemas. Hasta un próximo encuentro virtual, un abrazo.
Gracias por tus comentarios, apoyo y buenos deseos.
Te deseo un Feliz Año Nuevo en la paz y armonía de tu hogar. Que este año nuevo sea de mucha salud y bienestar para tu familia y seres queridos.
Saludos y fuerte abrazo para todos.
😃💕igual amigo.Que el 2025 nos arrope en salud,amor,paz,prosperidad.