SLC-S22W2/Equations and inequalities.
Hello My dear friends, I hope everyone is well? Alhamdulillah! I am also well with your prayers and love.
I am @sheikhtuhin
From #Bangladesh
 |
|---|
| Edit by inshot |
|---|
Dear friends, today I will be joining "Steemit Learning Challenge Season 22 Week 2//Equations and inequalities"I'm inviting these few friends of mine to join me here.
@shadow04 @abdulmomin @sohag10 @mahmud552
Task 1 Explain difference between linear and quadratic equations. Provide examples of each type of equation and describe their general forms. |
|---|
Difference between linear and quadratic equations:
| Linear equation | Quadratic equation |
|---|---|
| 🔲The highest power of the variable is 1. | 🔲The highest power of the variable is 2. |
| 🔲On a two-dimensional plane, it represents a straight line. | 🔲On a two-dimensional plane, this represents a parabola |
| 🔲Its general form is ax + b = 0, where a and b are constants and a ≠ 0. | 🔲Its general form is ax² + bx + c = 0, where a, b, and c are constants and a ≠ 0. |
| 🔲Example:- 2x + 3 = 7, -5y = 10 | 🔲Example:- x² - 4x + 3 = 0, 2y² + y - 1 = 0 |
Linear equation Explanation:
In a linear equation, the unknown quantity (x or y) appears only once and its highest power is 1. It is represented by a straight line.For example:
I have 5 pens. If you buy x more pens, the total number of pens will be 10. This problem can be written as an equation: 5 + x = 10.
Quadratic equation Explanation:
In a quadratic equation, the highest power of the unknown is 2 and it is represented by a parabola.For example:
The length of a side of a square is x units. If the area of the square is 25 square units, the equation would be: x² = 25.
Task 2 Describe two different types of inequalities(Which are not explained in course). Provide examples of each type of inequality and explain how to solve them. |
|---|
At this point I will give examples of two different types of infinity, of course not mentioned here.In this case, I have chosen two different types of inequalities:
- Absolute value inequality.
- Infinite inequality
Absolute value inequality:
Absolute value is the distance of a number from zero.The absolute value of any number is the positive value of that number.
For example:
|3|=3 , |-3|=3
The absolute value symbol (| |) is used in absolute value inequalities.
Example:
|X|<3
|2X-1|≥5
|X+4|≤2
Rules for solving:
- First, we need to split the inequality into two equations.
For example,
|X|<3 means -3<X<3
|X|>3 means X<-3 or X>3
- Each equation must be solved separately.
For example, we can write,
For |X|<3 -3<X<3.
Now we can solve these two inequalities nicely.
- It is possible to show it visually by expressing it on a number line.However, in this case, expressing the solution on a number line is optional.
Infinite inequality
An infinite inequality is a mathematical concept that uses infinity (the ∞ symbol) to express the relationship between two quantities.
For example:
x > ∞
- This inequality implies that the value of x will be greater than infinity, meaning that x can be any positive number.
-∞ < y ≤ 5
- This inequality implies that the value of y will be between -∞ and 5, meaning that y can be any real number.
Rules for solving:
In fact, it is not possible to solve an infinite inequality specifically because it is just a concept and not seen as a specific number.It has no limits, it will continue forever, which is never known.
Task 3 Solve the following linear equation: 2x + 5 = 11.Show step-by-step solution and share its practical example of how this equation can be applied in real life scenario. |
|---|
2x + 5 = 11
I will try to solve the equation step by step, InshaAllah.I'll first show you a picture of the solution I'm working on in my notebook.
I will do today's solution in two steps, although I have a very simple method, I will adopt two steps to present it in a somewhat unique way.
 |
|---|
2x + 5 = 11
=> 2x + 5-5 = 11-5
=> 2x=6
=> 2x/2= 6/2
=> X=3 (Ans)
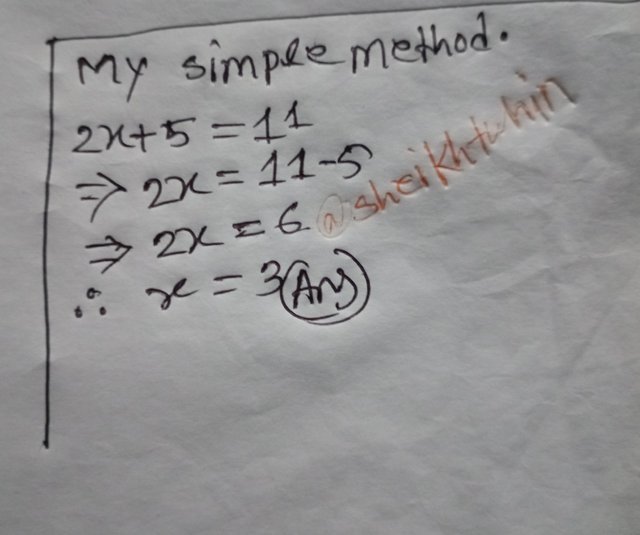 |
|---|
My simple method:
2x + 5 = 11
=> 2x=11-5
=> 2x=6
=> X=6/2
X=3

Application in real life:
Suppose,
I bought 2 apples. Each apple cost x rupees and I spent a total of 11 rupees.And 5 taka is the price of any other fruit.
- If we write it in equation form, we get:
2x + 5 = 11 - Where by solving we get the solution given above.
Task 4 Scenario: Tom's Bakery |
|---|
Tom's bakery is a most famous bakery of tow and it's famous for its yummiest pastries and bread. Tom which is owner want for making sure that he has sufficient ingredients for meeting needs for his famous chocolate cake and chocolate cake recipe needs 2 cups of flour, 1 cup of sugar and 1/2 cup of cocoa powder for each cake.
| Equation | If Tom wants for making x cakes and he has 10 cups of flour, 8 cups of sugar and 4 cups of cocoa powder then calculate number of cakes that can be made by Tom? |
|---|
Solution:
 |
|---|
Ingredients needed for every cake:
| 2 cups flour | 1 cup sugar | 1/2 cup cocoa powder |
Equation according to the element:
Step-1:
Flour required for each cake = 2 cups
Tom has flour = 10 cups.
"X" cake needs flour,
2x=10
=>X=10/2
=> X=5
Tom can make 5 cakes based on the dough.
Step-2:
Sugar required for each cake = 1 cup
Tom has sugar = 08 cups
"X" Sugar is needed for the cake.
X=8/1
X= 8
Tom can make 8 cakes based on sugar.
Step-3:
Cocoa powder required for each cake = 1/2 cup
Tom has total cocoa powder = 4 cups.
Cocoa powder is needed to make "X" cake.
1/2 x = 4
=> X/2=4
=> x= 2*4
X=8
Tom can make 8 cookies based on cocoa powder.
Final decision:
We have determined the ability to create based on three elements.Since the flour will run out after making five cakes, it is possible for Tom to determine the maximum number of cakes that can be made.
| Inequality | Tom wants for making sure that he has sufficient sugar for meeting needs for his chocolate cake. He also knows that each cake needs 1 cup of sugar and he has 8 cups of sugar which are available. He also knows that he wants to make at least 6 cakes. |
|---|
Solution:
 |
|---|
Step-1:
Hold on,
Tom wants to make = X cake.
For each cake, you need = 1 cup of sugar.
So, X cake needs = X cups of sugar.
Step-2
Tom has = 8 cups of sugar.
So, the sugar needed to make X cake is less than or equal to 8 cups.
= X≤ 8
Step-3
The number of cakes will be at least 6.
So,
X≥6
Step-4
Now we will combine these two conditions.
(1). X≤8 (where sugar content is limited)
(2). X≥6 (where the number of cakes is at least 6)
According to the conditions,
6 ≤ x ≤ 8
Decision:
Here Tom can make a maximum of six cakes and a minimum of six cakes since the question asked whether Tom could make six cakes.Of course, Tom has enough sugar to make six cakes.
Scenerio: Number of gallons Ashley needs. |
|---|
Suppose there's a person named Ashley who is planning for a road trip from City A to City B.If I talk about distance between two cities then it's around 240 miles. Ashley's car fuel tank have ability of holding 12 gallons of Suppose that his car gets 20 miles for each gallon then how many gallons of gas may Ashley purchase if he already has 2 gallons in his tank and he wants to have minimum 1 gallon left over when he arrives at City B?
| Equation | Let's consider x as number of gallons of gas Ashley can purchase. |
|---|
 |
|---|
Solution:
Step-1
Hold on,
Amount of gas Ashley will buy = X gallons
Then total gallons of gas=
X+2 gallons
step-2
Total gas needed। = 240 miles
Runs per gallon of gas= 20 Miles
So, the gas needed to go 240 miles is =
240/20
=12 Gallon.
Step-3
The total amount of gas to keep one gallon of gas =12-1
=11 Gallon
Step-4
Ashley already has gas = 2 gallons
He needs to purchase X gallons to reach =
X+2=11----(1)
| Solving the above equation, we get |
|---|
X+2=11
=>X+2-2=11-2 [Subtract 2 from both sides]
=> X=9
Decision making:
Ashley needs to buy 9 more gallons of gas to reach her desired goal.
| Inequality | x + 2 ≥ (240/20) - 1 |
|---|
 |
|---|
Solution:
Step-1
First, let's calculate,
240/2
=12
Then the inequality, = X+2≥12-1
Step-2
From the equation obtained from the first step, we subtract one from 12.
X+2≥12-1
=>X+2≥11
Step-3
To find the value of "X", we subtract 2 from both sides of the equation.
X+2-2≥11-2 [Subtract 2 from both sides]
=>X≥9
Decision making:
Ashley needs to buy at least 9 gallons of gas so that she can get from city A to city B and still have one gallon of gas left.

Many thanks to @khursheedanwar sir.Because of this, I had the opportunity to practice those topics again, even near the end of my studies, after going through these algebra chapters.However, to elaborate on these points, I had to take help from higher mathematics books and spent 24 hours editing this post.
Thank you very much everyone |
|---|
X promotion
https://x.com/sheikhtuhin24/status/1871591154653057203?t=1htR97Pw2UDkhOAiQpRyAQ&s=19
🤗 @sheikhtuhin - fantastic content as always! 🎯 ⭐
Hey friend! 🎉 Come check out your awesome post on my shiny new front-end! It's still a work in progress but I'd love to hear what you think! View your post here ✨
I would like to request you to please change task 4, second part about drawing calculator and replace it with this task!
• Scenerio: Number of gallons Ashley needs.
You have to solve for inequality now for finding minimum number of gallons of gas Ashley required to purchase.
Actually due to an error it was not showing in post now now I have edited my post!
I am really sorry for this!
Once you are done you can inform me so that I may review your post timely
Thank you very much @khursheedanwar sir.I had done it this way at the beginning, but after some time I saw an update and a picture of a calculator was asked for, so I solved it and left it.Thanks for telling me I have already removed the calculator picture and added the second task.