"SLC-S22W2/Equations and inequalities."
Designed by Pixellap
Good morning fellow steemians today I'll be participating on "SLC-S22W2/Equations and inequalities." organized by @khursheedanwar
I must say it has really been an amazing and interesting course starting from SLC22 week 1 and now to week 2.
TASK 1 |
|---|
Linear and quadratic equations are two fundamental types of algebraic equations, but they differ in their degree, graph representation, and solutions.
Linear Equation :A linear equation represents a straight line on a graph. It is called "linear" because the highest power of the variable is 1. Linear equations have a constant rate of change and involve no curvature.
General forms of a linear Equation are ;
ax+b=0
Where
a and b are constant
x is the variable
a cannot equals to 0
Examples :
4x+3= 0
Quadratic equation :A quadratic equation represents a parabola (a U-shaped curve) on a graph. It is called "quadratic" because the highest power of the variable is 2. Quadratic equations can open upwards or downwards depending on the sign of the leading coefficient.
General form of a quadratic equation
bx²+ax-d=4
b,a,d are constants
x is a variable
a cannot equals to 0
Example
x²+4x-3=0
Key differences |
|---|
| Aspect | Linear Equation | Quadratic Equation |
|---|---|---|
| Highest power | 1 | 2 |
| Number of Roots | 1 root | up to 2 root |
| Graph shape | Straight line | parabola(I shape) |
| General form | bx+a=0 | ax²-bx+c=0 |
| Example | 4x+a=0 | x²+4x+2=0 |
TASK 2 |
|---|
Below I'll be giving out two different types of inequalities and I'll also be explaining more on it and also giving examples of it
- Absolute value Inequality :An absolute value inequality is an inequality that involves the absolute value of a variable or expression,the absolute value of a number represents its distance from zero on a number line, regardless of direction. An absolute value Inequality can be linear or quadratic depending on the inequality we are dealing with.
There are two major types of Absolute value Inequality, they're
- Less than (|x|<a):this means a the value of x is within a distance a from 0, it can also be written as a compound Inequality
-a<x<a
-2<x<2
- Greater than (|x|>a):this means that the value of x is more than a distance a from 0, it can be rewritten as two separate inequalities
x<-a or x>a
x<-2 or x>2
Solving an Absolute value Inequality
Example:|4x -5|<=9
Solution
There are two approach of solving this. Theory States that the magnitude sign cancels out any negative, so it's simply a symbolic+ or -. So we can separate the equation as such and solve them independently and have a unique solution by using the number line.
On solving this equation , I'll square both side of the equation to get away with the magnitude sign and then resolve it.
I'll be starting with the first method
|4x -5|<=9
The + method
Removing the brackets,
(4x -5)<=9
4x -5<=9.
Balance the equation by adding 5 on both side of the equation from both sides.
4x -5+5<=9+5.
4x <= 14
Divide both side of the equation by 2.
x <= 7.
The - signs
(4x -5)<=9
Opening the bracket and multiplying the negative if the content inside, we have.
-4x + 5 <=9
Subtracting 5 from both side of the equation, we have
-4x + 5 - 5 <=9- 5
-4x <= 4
multiplying both sides of the equation By -1 first, transform the equation to.
4x >= -4
After multiplying both side by -1 we can notice that the sign has changed. Which means that the equation have been reversed. So now we'll be divide both side of the equation by 4 , who is equals to
x>=1
- Quadratic Inequalities:
This is a type of inequality in which a quadratic expression is involved. They are generally Written in the form of ax² + bx + c >, <, ≥, ≤ 0.
Where a, b, c are the constants while x is the variable.
Example 1.
x² + 4x + 4 > 0
Solution
We will need to factorize the quadratic expression to solve this inequality
= (x + 2)² > 0
Therefore, the inequality is true for values of x except x = -2.
TASK 3 |
|---|
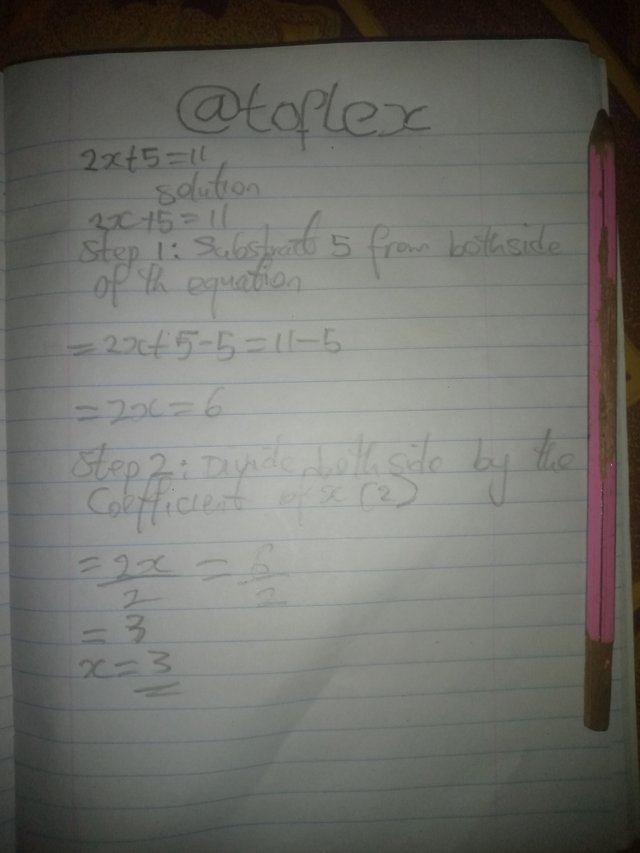
In Real Life Scenario |
|---|
@toflex bought gas for his car at the rate of 5steem with additional 2 STEEM per kilogram. Given that the total gas @toflex bought for his car is 11 Steem for a kilogram, calculate the total kilogram he bought for his car
Solution |
|---|
Let x = kilogram
Extra 2steem per kilogram= 2x
Initial amount of gas bought = 5steem
Total amount of gas= 11steem
Total amount of gas bought= initial amount of gas bought+ extra charge per kilometers.
==> 2x + 5 = 11
Subtracting 5steem from each
2x = (11 - 5)
2x = 6
Divide by 2
x = 3
Therefore total amount of kilogram of gas he bought for his car was 3 kilogram
SCENARIO - TOM'S BAKERY |
|---|
EQUATION |
|---|
Ingredients required per cake.
2 cups of flour.
1 cup of sugar..
0.5 cup of cocco powder.
This are available ingredients to be used.
10 cups of flour
8 cups of sugar and
4 cups of cocoa powder.
Number of cake per ingredients
flour
2 cups of flour for 1 cake.
10 cups of flour for x cakes
X = 10/2 = 5 cakes to be made
sugar.
1 cups of sugar for 1 cake.
8 cups of sugar for x cakes
X = 8/1 = 8 cakes
cocoa powder.
0.5 cups of cocoa powder for 1 cake.
4 cups of cocoa powder for x cakes
X = 4/0.5 = 8 cakes.
So Tom can only make maximum of 5 cakes with the available resources. Therefore x = 5 cakes.
INEQUALITY |
|---|
Let X represent the number of cakes Tom wants to make
flour
2x <= 10
sugar
1x <= 8
Cocoa powder
0.5x <= 4
at least 6 cakes
x>= 6
With the available resources, Tom is capable to make at least 6 cakes, For the available resources, x !<=5 but x>= 6
Now for sugar/ cocoa powder, x <= 8.
So they took conditions for this to be possible is
{x>= 6,
{ x <= 8.
2nd SCENARIO |
|---|

SOLUTION |
|---|
Let x represent number of gallons Ashley can purchase.
Distance between two city = 240 miles
Consumption = 1 Gallon /20 mile.
Considering the first given inequality
x + 2 >= 240/20 - 1
240/20 = 12 gallons
x + 2 >= 12 -1
The equation transform to
x + 2 >= 11
Subtract 2 on either sides
x + 2 - 2 >= 11 - 2
x >= 9
Ashley will have to purchase at least 9 gallons of gas to reach city be and be left with 1 gallon extra.
It was really an amazing learningchallenge to participate and I really appreciate@khursheedanwar for his time ,so I'll be inviting some of my steemit friends to participate on "SLC-S22W2/Equations and inequalities."; @jozzie90,@bessie2023,@bossj23
My x promotion