"SLC-S22W3//Equations and Systems of equations."

Hello friends and followers of STEM content, in this case specifically algebra.

This time is my second algebra challenge hosted by professor @khursheedanwar on equations and systems of equations.

In my case I consider systems of equations very important, since I have to recognize that in my profession petroleum engineering systems of equations help us to be able to simulate the behavior of certain physical phenomena that occur at the level of the oil reservoir in terms of productivity and transport of gas and oil flow.

I would dare to say that many of the users who are here in their different professions know that the systems of equations are of great help even in decision making in any problem in the professional branch that is.

• Task 1

Explain difference between linear and non linear systems of equations. Provide examples of each type of system of equation and describe their general forms.

The first important thing is to give some associated concepts, and then analyze some differences between the two systems of equations.

Systems of linear equations: It is called a system of equations because it is formed by a set of linear equations, these linear equations can be formed by several variables, the number of variables of the system of linear equations determines if the system of linear equations represents a matrix whose size is determined by rows and columns, for example:

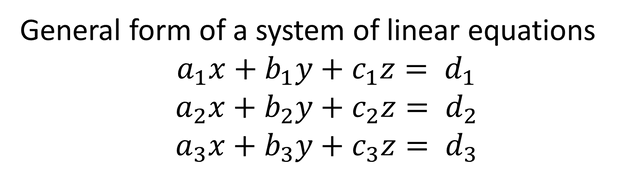
The previous example invites us to analyze that since the system has three variables (X Y Z) and has three linear equations, then it could represent a square matrix of size 3 x 3, i.e. three rows and three columns, as shown:

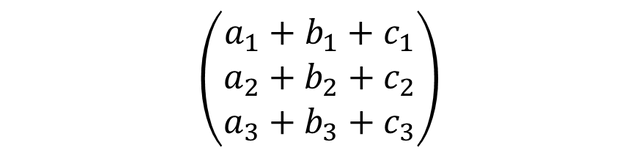
We could also add that certain algebraic operations with these matrices are performed with the intention of solving the system of equations that they may represent.

Who can be a,bc,d?

a,b,c,d can be real numbers that accompany the variables X, Y, Z, while the variables X, Y, Z, are characterized by being raised to the exponent one, that is to say they are first degree powers, hence they are considered systems of linear equations.

Systems of nonlinear equations: It is a system of equations where one of the terms of the equations that conforms it is not linear, that is to say, it can be a quadratic, cubic, trigonometric, logarithmic, exponential term, in short, if at least one term is nonlinear it is more than enough to affirm that it is a system of nonlinear equations. Another condition that makes the system of equations nonlinear is that there is a product of variables.

In the case of the general form of a system of nonlinear equations there is no general form to represent a system of nonlinear equations, since as it was said in the definition, with only one term being nonlinear, it can already be characterized as a system of nonlinear equations, therefore a system of nonlinear equations can take different forms.

An example of a nonlinear system of equations can be:

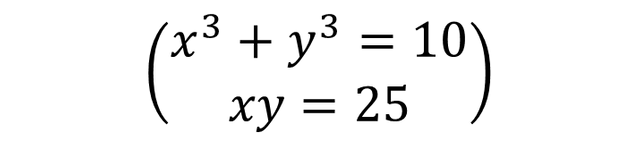
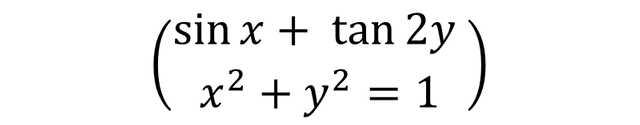
Differences between linear vs. nonlinear equations

In summary it can be said that the main difference between the systems of linear equations and the systems of nonlinear equations are the form and structure, since the systems of linear equations all their variables are of first degree, while the nonlinear ones can have a nonlinear variable.

At the same time by having different degrees of power in their variables, the solutions represent different graphs, in the linear equation system the solutions represent the intersections of straight lines, while in the nonlinear equation systems the solutions represent the intersections of other graphs such as parabolas, hyperbolas, circles, among others.

The methods to solve these systems of equations, result in that they are more complex to solve the systems of nonlinear equations, since the systems of linear equations use simple methods such as substitution, elimination, or even methods to solve matrices.

It is important to emphasize that if in a system of linear equations the straight lines can be plotted at the points where the straight lines intersect, those points are the solution of the system of equations, in the case of the system of nonlinear equations, where the curves intersect, that will be the solution of the system of nonlinear equations.

Example 1

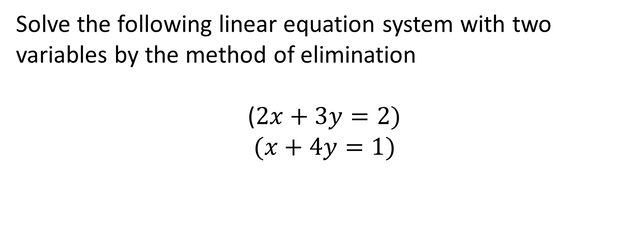
To apply the elimination method we simply multiply the equation number (1) by 1 and the equation number 2 we multiply it by -2, with this we get to eliminate the variable x, and we can find the value of the variable Y, as I show below:

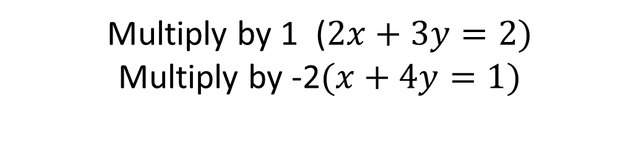
Therefore it remains:

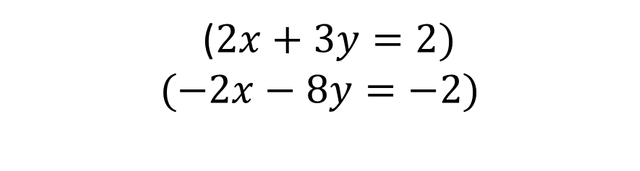
We cancel 2x - 2x, because it is equal to zero, so it remains:

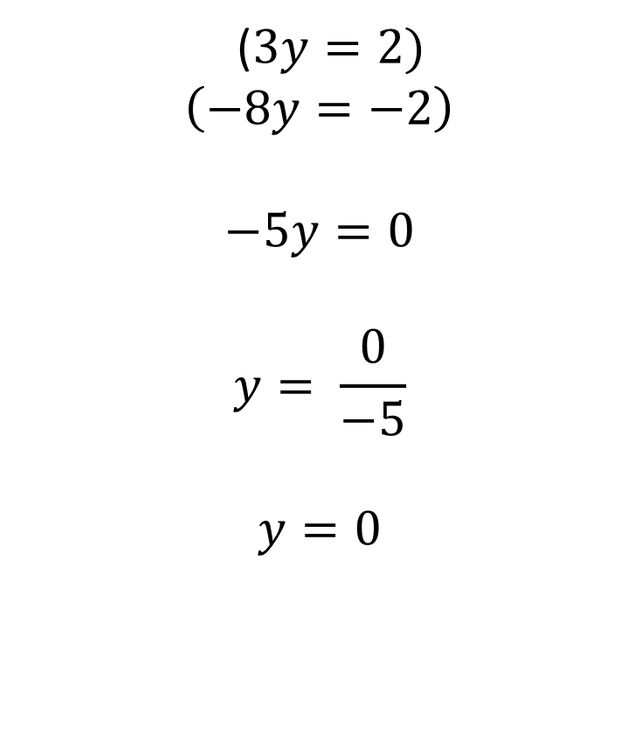
The first variable that we got its solution was Y = 0.

To get the value of X by the elimination method, we multiply -4 by equation 1, and multiply equation 2 by 3, as shown below:

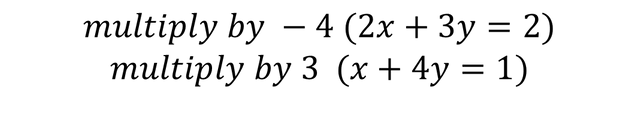
What is sought is to cancel the variable Y and get the value of the solution of the variable X, so it looks like this:

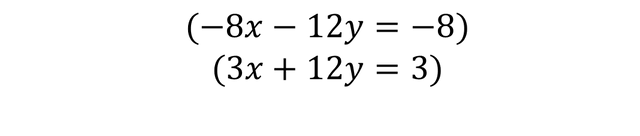
The Y variable is cancelled and remains:

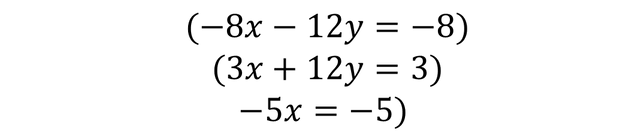
Then the -5 that accompanies the variable X and that is multiplying goes to the other side of the equality to be divided and remains:

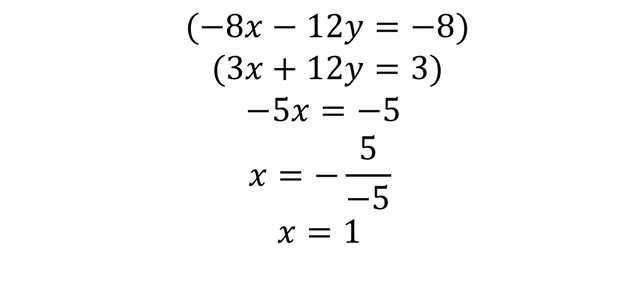
The value of the variable X = 1

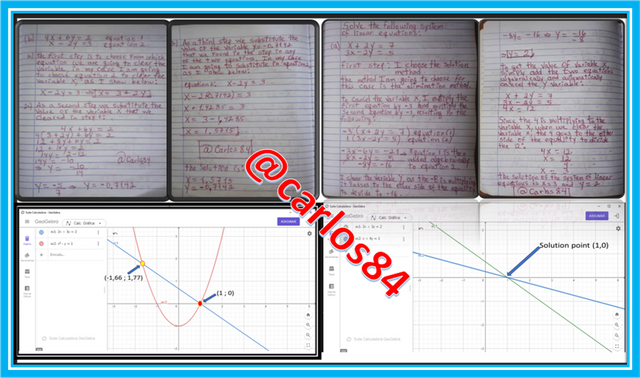
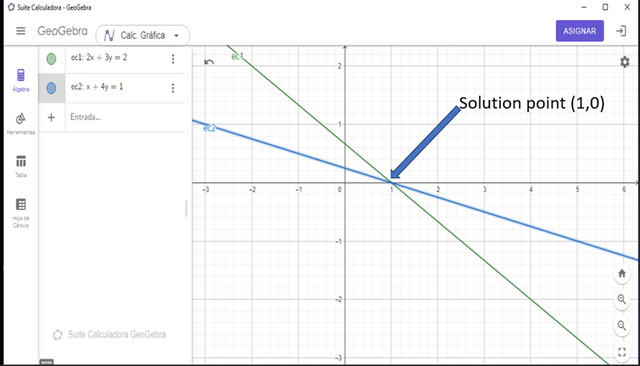
What it means is that this system of linear equation that I am explaining as an example has its point of intercept between the two lines at the point (1,0), we can corroborate it using the geogebra software:

Example 2

The first important thing to highlight in this second example is that this type of equation, being nonlinear, cannot be solved by the elimination method, since it is not possible to eliminate terms that have different degrees in their powers, therefore the solution that we are going to apply is the substitution method:

The first step of the substitution method is to clear a variable from any of the two equations, either equation 1 or equation 2, for this case I will select to clear the variable Y from equation 2, therefore we are left with:

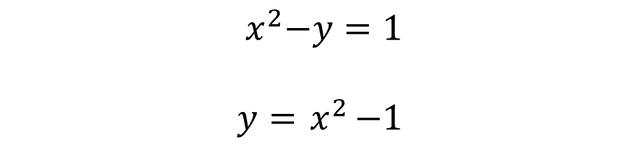
Since we have already cleared the variable (Y) from equation 2, what we have to do is to substitute the value of 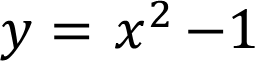in equation 1

What we are left with is a second degree equation, so what remains is to find the solution of this second degree equation by applying the following formula:

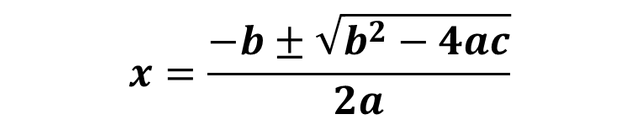
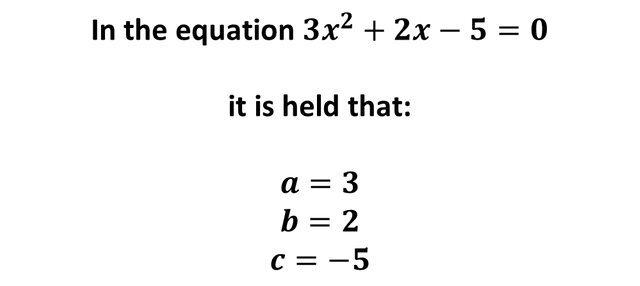
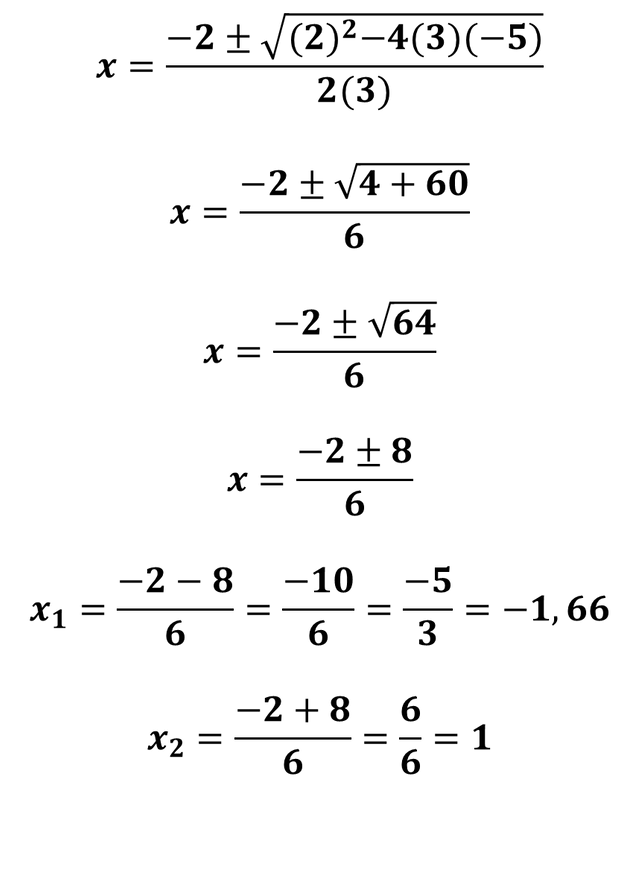
The solution for this nonlinear equation system is X1= -1.66 and X2= 1, therefore if we make the substitution of X1 and X2 in any of the two equations (equation1 and equation2), it will give us as a solution two values of Y, which are Y1 and Y2, I will select to substitute in equation 1, although it is different where we make the substitution, therefore:

The solution of this nonlinear equation system is:

X1 = -1.66
X2 = 1
Y1 = 1.77
Y2 = 0

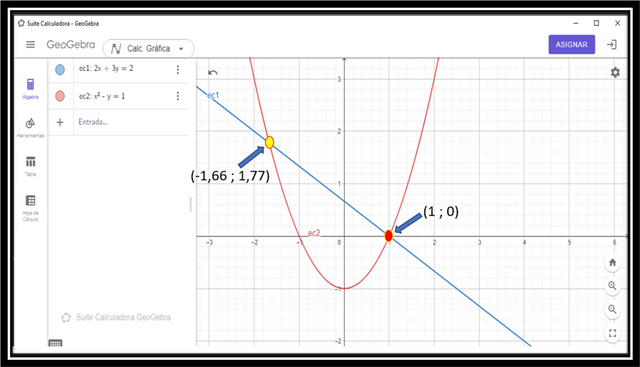
Which means that equation 1 representing a line in the plane, and equation 2 representing a parabola in the plane intersect at the points :

(-1.66 ; 1.77)

(1 ; 0)

This can be corroborated in the graph generated by the geogebra software:

• Task 2

• Describe any one method for solving system of linear equations and share atleast one step by step algebric example.

(It should be other than substitution, elimination and graphing method)

To solve task 2, I am going to choose Cramer's method also called the method of determinants, this method I am going to apply it to solve a system of linear equations of size 2x2, the system of equation that I am going to solve is the following:

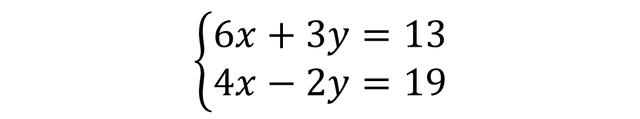
The cramer's method tells us that the solution value of the variable X is equal to the following formula:

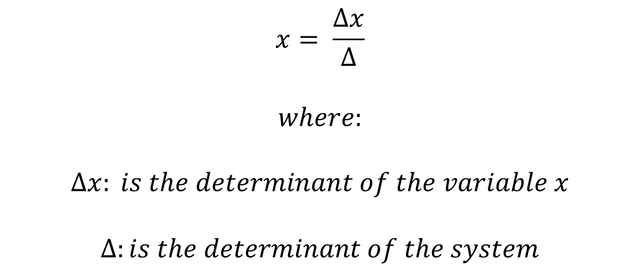
Cramer's method tells us that the solution value of the variable Y is equal to the following formula:

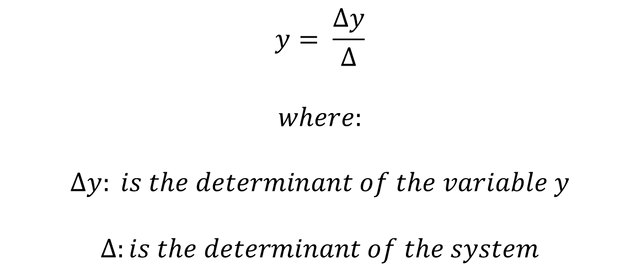
If we have a generalized matrix of size 2x2 of the following form:

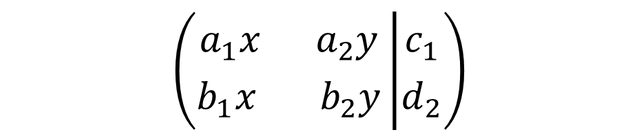
Therefore the determinant of the system (∆) is calculated as follows:

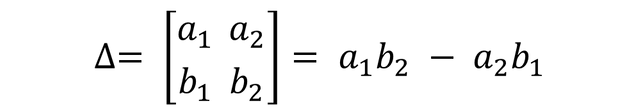
Therefore if we calculate the determinant of the system we are left with:

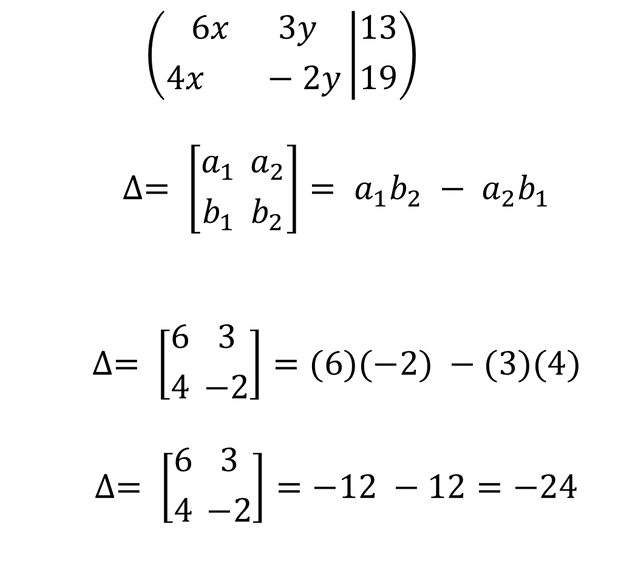
We now proceed to calculate the determinant of X (∆X), knowing that the determinant of X (∆X) has the following formula:

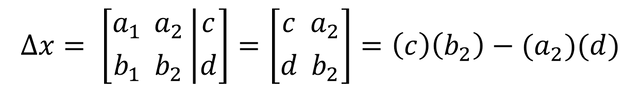
Therefore if we calculate the determinant of X we are left with the following:

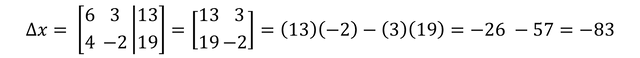
Having already calculated the determinant of the system and the determinant of X, we can calculate the solution for the value of the variable X:

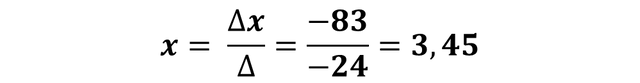
Therefore if we calculate the determinant of Y we are left with the following:

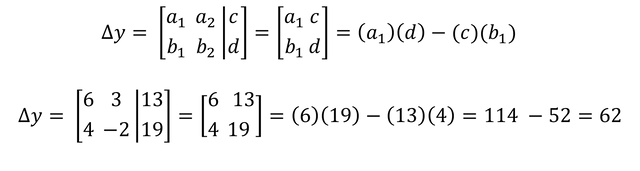
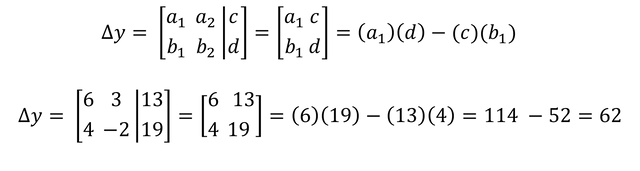
Since we have already calculated the determinant of Y and the determinant of the system, we can calculate the solution value of the variable Y as follows:

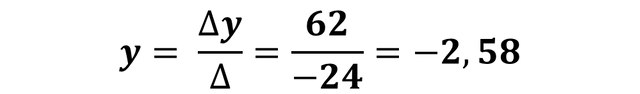
Lo que significa que este sistema de ecuación lineal tiene como solución:

X= 3.45
Y= -2.58

• Task 3

• You need for solving following system of linear equations:

(a)

x + 2y = 7
3x - 2y = 5

(b)

4x + 6y = 2
x - 2y = 3

(You are required to solve these problems at paper and then share clear photographs for adding a touch of your creativity and personal effort which should be marked with your username)

I am going to solve the first system of linear equations by the elimination method, as shown below:

I am going to solve the second system of linear equations by the substitution method, as shown below:

• Task 4

Scenario number 1

Suppose there's a company producing two products, A and B.If cost of producing x units of A and y units of B is given by system then;

2x + 3y = 130 (cost of materials)
x + 2y = 110 (cost of labor)

If company wants for producing 50 units of product A then calculate how much units of product B they may produce?

(Solve the above scenerio based questions and share step by step that how you reach to your final outcome)

For this scenario A=X and B=Y

So if you ask how many units of B can be produced if 50 units of A are produced, it implies that X= 50 units.

Also keep in mind that total cost = material costs + labor costs.

So the equation representing total costs is: 3x + 5y = 240, when X = 50 implies that:

3(50) +5y = 240

150 + 5y = 240

despejamos la variable Y:

5y = 240 - 150

5y = 90

y = 90/5

y = 18

Lo que significa que para poder cubrir un costo total de 240 y producir 50 unidades de A, es necesario que se puedan producir 18 unidades de B.

Scenario number 2

• Suppose there's a bakery producing two types of cakes which are vanilla and chocolate.If cost of producing x cakes of vanilla and y cakes of chocolate is given by system then;

x + 2y = 80 (cost of ingredients)
2x + y = 70 (cost of labor)

If bakery wants for producing 30 cakes of vanilla then calculate how much cakes of chocolate can they produce?

For this scenario the total cost to produce vanilla and chocolate cakes is governed by the algebraic sum of the linear equation system, so the following remains:

3x + 3y = 150

If you want to produce 30 vanilla cakes, how many chocolate ones can you produce?

X = vanilla cakes
Y = chocolate cakes

Implies that:

3 (30) + 3y = 150

90 + 3y = 150

3y = 150-90

3y = 60

y = 60/3

y = 20

This means that in order to have a total cost of 150 and produce 30 vanilla cakes, 20 chocolate cakes must be produced.