Linear Search vs Binary Search
Software engineers often use various algorithms in order to accomplish certain tasks. One such task that a programmer often faces is searching for elements in a container of some sort. In face it is one of the fundamental algorithms of computer science. Searching algorithms are very important and so commonly used, it is important to know how to optimize said algorithms or use the proper implementation. In this post we will briefly be looking at two very common reoccurring searching algorithms and analyze their time complexity.
What is time complexity and why is it important? Software engineers often use the term time complexity to represent time taken to run a particular algorithm. Time complexity is often measured in operations preformed by the code assuming that each operation takes a fixed amount of time. There are various cases of time complexity, the most important (for me at least) is Big-O notation. For now we will only use Big-O, but soon hopefully cover other cases of time complexity and their uses in another post. Why use Big-O notation to represent our time complexity? Big-O is often refereed to as the worst case which is helpful when trying to evaluate the maximum computation time taken. I will not cover the mathematical background for evaluating time complexities in this post, however there are many places where you can learn to calculate time complexity for your own algorithms.
Linear Search
The first searching algorithm we will look at is the linear search. Linear search is one of the first algorithms many programmers learn, partly because it is short and simple to code. Linear search functions by sequentially checking each element in a given list until a match with the search value is found or until the entire list has been checked. This can be implemented with a single for loop and a nested if statement.
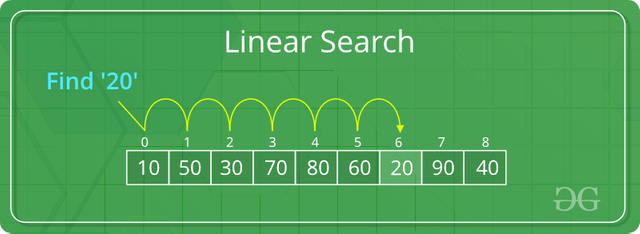
With this being said, if a list of size N was given to the algorithm to search for a element, the worst possible case is that our element is not present in the list. Thus the algorithm searches the entire list of N items. Therefore our time complexity can be denoted as O(N). This means our algorithm takes at most N operations in order to complete. However, we can improve upon this and speed things up.
Binary Search
Introducing another commonly used search algorithm by software engineers, binary search. Unlike linear search, binary search is more complex and often uses techniques such as recursion when implementing. During a binary search, the algorithm divides the list of items in half each iteration and preforms a check. If the search value is less than the mid element's value we take the first half of the list, else if it is larger we take the back half. This is repeated over and over again until our search value only remains or it is not found. Because we are comparing the search value against the mid element's value, it is important that the list of elements is sorted before calling the search function. This is one of the drawbacks of using a binary search implementation.
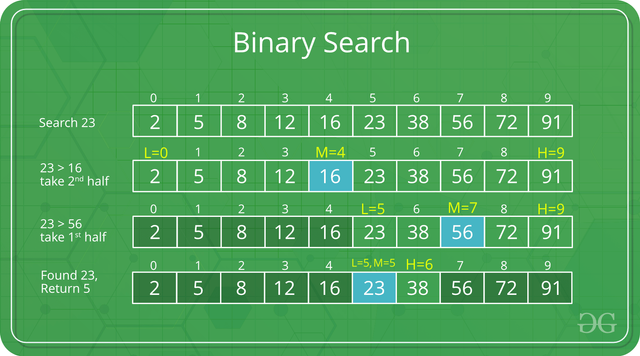
Compared to the linear search's O(N) time complexity, binary search has O(logN) time complexity. Instead of checking each element in a linear fashion, we divide our list of elements in half until we find our element. A good explanation can be found here.
In conclusion based on our time complexity evaluation for both linear and binary search, we can determine which searching algorithm is better. Based on the graph below, binary search is clearly the winner in the long game.
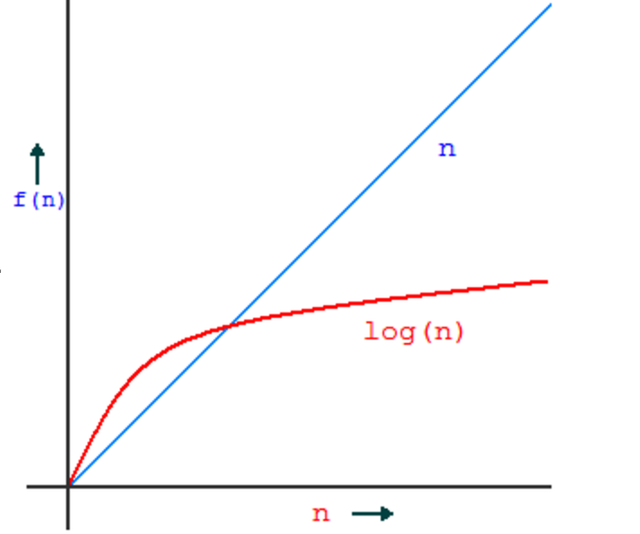
The growth of the linear search algorithm is linear and the growth of the binary search algorithm is logarithmic. This means while the linear function grows at a constant rate, the logarithmic function slows down significantly as the number of elements increases. Thank you for reading this post, if you would like a specific topic about programming that you would like me to cover feel free to comment below. Questions or concerns? Also comment below!
Other Links/Resources: