Bitcoin mining by hand.
Someone decided to mine manually. Here is the whole story.
It turns out that the SHA-256 algorithm used for mining is pretty simple and can in fact be done by hand. Not surprisingly, the process is extremely slow compared to hardware mining and is entirely impractical. But performing the algorithm manually is a good way to understand exactly how it works.

In Bitcoin, a successful hash is one that starts with enough zeros. Just as it is rare to find a phone number or license plate ending in multiple zeros, it is rare to find a hash starting with multiple zeros. But Bitcoin is exponentially harder. Currently, a successful hash must start with approximately 17 zeros, so only one out of 1.4x1020 hashes will be successful. In other words, finding a successful hash is harder than finding a particular grain of sand out of all the grains of sand on Earth.
The SHA-256 hash algorithm takes input blocks of 512 bits (i.e. 64 bytes), combines the data cryptographically, and generates a 256-bit (32 byte) output. The SHA-256 algorithm consists of a relatively simple round repeated 64 times. The diagram below shows one round, which takes eight 4-byte inputs, A through H, performs a few operations, and generates new values of A through H.
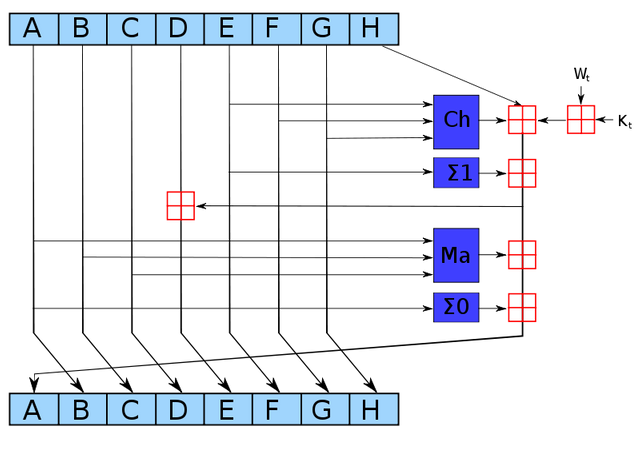
The blue boxes mix up the values in non-linear ways that are hard to analyze cryptographically. Since the algorithm uses several different functions, discovering an attack is harder. (If you could figure out a mathematical shortcut to generate successful hashes, you could take over Bitcoin mining.)
The Ma majority box looks at the bits of A, B, and C. For each position, if the majority of the bits are 0, it outputs 0. Otherwise it outputs 1. That is, for each position in A, B, and C, look at the number of 1 bits. If it is zero or one, output 0. If it is two or three, output 1.
The Σ0 box rotates the bits of A to form three rotated versions, and then sums them together modulo 2. In other words, if the number of 1 bits is odd, the sum is 1; otherwise, it is 0. The three values in the sum are A rotated right by 2 bits, 13 bits, and 22 bits.
The Ch "choose" box chooses output bits based on the value of input E. If a bit of E is 1, the output bit is the corresponding bit of F. If a bit of E is 0, the output bit is the corresponding bit of G. In this way, the bits of F and G are shuffled together based on the value of E.
The next box Σ1 rotates and sums the bits of E, similar to Σ0 except the shifts are 6, 11, and 25 bits.
The red boxes perform 32-bit addition, generating new values for A and E. The input Wt is based on the input data, slightly processed. (This is where the input block gets fed into the algorithm.) The input Kt is a constant defined for each round.[2]
As can be seen from the diagram above, only A and E are changed in a round. The other values pass through unchanged, with the old A value becoming the new B value, the old B value becoming the new C value and so forth. Although each round of SHA-256 doesn't change the data much, after 64 rounds the input data will be completely scrambled.
To explain what's on the paper: I've written each block A through H in hex on a separate row and put the binary value below. The maj operation appears below C, and the shifts and Σ0 appear above row A. Likewise, the choose operation appears below G, and the shifts and Σ1 above E. In the lower right, a bunch of terms are added together, corresponding to the first three red sum boxes. In the upper right, this sum is used to generate the new A value, and in the middle right, this sum is used to generate the new E value. These steps all correspond to the diagram and discussion above.
I also manually performed another hash round, the last round to finish hashing the Bitcoin block. In the image below, the hash result is highlighted in yellow. The zeroes in this hash show that it is a successful hash. Note that the zeroes are at the end of the hash. The reason is that Bitcoin inconveniently reverses all the bytes generated by SHA-256.
Conclusion
The SHA-256 algorithm is surprisingly simple, easy enough to do by hand. (The elliptic curve algorithm for signing Bitcoin transactions would be very painful to do by hand since it has lots of multiplication of 32-byte integers.) Doing one round of SHA-256 by hand took me 16 minutes, 45 seconds. At this rate, hashing a full Bitcoin block (128 rounds) would take 1.49 days, for a hash rate of 0.67 hashes per day (although I would probably get faster with practice). In comparison, current Bitcoin mining hardware does several terahashes per second, about a quintillion times faster than my manual hashing. Needless to say, manual Bitcoin mining is not at all practical.
A Reddit reader asked about my energy consumption. There's not much physical exertion, so assuming a resting metabolic rate of 1500kcal/day, manual hashing works out to almost 10 megajoules/hash. A typical energy consumption for mining hardware is 1000 megahashes/joule. So I'm less energy efficient by a factor of 10^16, or 10 quadrillion. The next question is the energy cost. A cheap source of food energy is donuts at $0.23 for 200 kcalories. Electricity here is $0.15/kilowatt-hour, which is cheaper by a factor of 6.7 - closer than I expected. Thus my energy cost per hash is about 67 quadrillion times that of mining hardware. It's clear I'm not going to make my fortune off manual mining, and I haven't even included the cost of all the paper and pencils I'll need.
@kartikohri1712 Thanks for sharing.
Worth reading.
thanks for support. resteem and share for such good content.
Hi! I am a robot. I just upvoted you! I found similar content that readers might be interested in:
https://gizmodo.com/mining-bitcoin-with-pencil-and-paper-1640353309