Blockchain & Cryptocurrency #9: Incentives and Proof-of-Work

In the previous post we saw the technical mechanism ruling Bitcoin protocol. Now we will go into further details regarding incentives and proof of work that encourage nodes to behave honestly.

Incentives to nodes

Assumption of honesty is problematic

Why do we expect that there are honest nodes in Bitcoin system? Can we give nodes any incentives for behaving honestly?

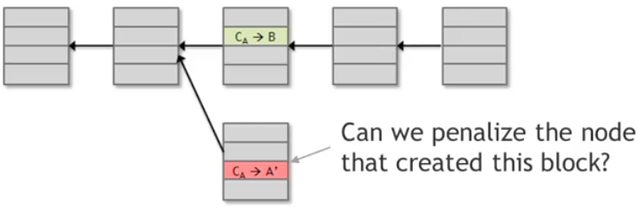
First of all we could think to penalyze nodes that try to cheat. For example in inserting double-spending transactions. But it is problematic to do that, mainly because nodes don't have identities. So there's no way to go after them and penalize them.

The only chance is to flip the question and see how it is possible to reward the honest nodes. The ones who created all the blocks that end up on the long-term consensus chain. We don't have node identity, so we can't mail them cash to their home addresses.

But Bitcoin is a currency and has a value, so we can use BitCoins in order to incentivize the nodes to behave honestly.

Incentive 1: Block Reward

When a node insert a new block in the blockchain, he contributes to the creation of new Bitcoins. In fact, each new block includes a special transaction of coin creation. The node that add the block can choose the recipient of these new coins, so it will typically choose its address. We can think of it as a payment in exchange for the service of creating that block.

It seems that a node gets the block award regardless of whether it proposes a block with only valid transactions, or it behaves maliciously. The node will collect the reward only if this block ends up on the long-term consensus branch. In fact, the creation transaction also becomes valid only if it belongs to a long-term consensus branch.

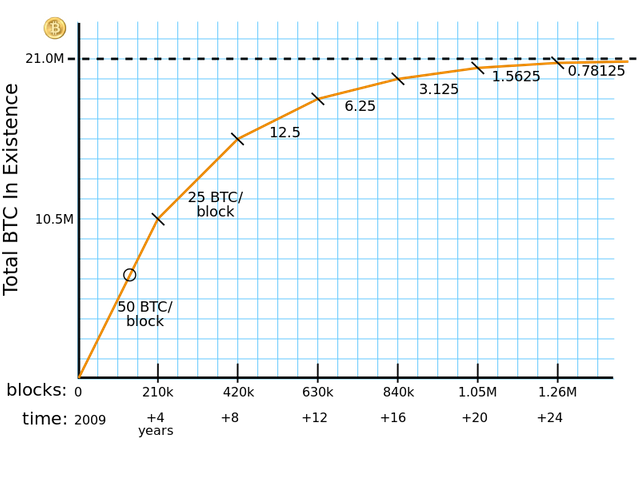
The amount of created coins has a special property. At July 2008 it was fixed at 50 Bitcoins, but it halves every four years. So, actually the reward is 12,5 Bitcoin and the last halving occurred on July 2016.

This halving phenomenon has some important consequences, as we can see in the previous graph of time (X-axis) versus the total number of BitCoins in circulation (Y-axis). It forms a geometric series, so there's a finite sum, a total finite supply of BitCoins. Adding up all these numbers based on the rate of new block creation (around 1 block every 10 minutes), it sums up to 21 million. And there's no other Bitcoin creation mechanism.

We could think that this will end up in an insecure system, because nodes will no longer have an incentive. But there's another source of income for honest nodes.

Incentive 2: Transactions fees

The creator of any transaction can choose to make the output value of that coin less than the input value.
Transaction fee = output_value - input_value
The node that inserts the new block receives, as a reward, all the fees of the transaction included in the block.
This transaction fee is purely voluntary. It is not mandatory to include a fee in a transaction, but as the block reward starts to run out, it will become almost mandatory for nodes to include a transaction fee in order to get a reasonable quality of service. How this system will evolve depends on a lot of game theory, which hasn't been fully worked out yet. So that's an interesting area of open research in BitCoin.

Remaining problems in Bitcoin Protocol

After understanding how incentives work, there are a few reamining problems in Bitcoin protocol:

1. how can we pick a random node to insert the new block?
2. after introducing incentives, everyone probably wants to run a Bitcoin node in order to get a reward
3. an adversary might try to create a whole bunch of Sybil nodes in order to try to subvert this consensus process

These three problems are all related one another and have the same solution: Proof of Work.

Proof of Work

Instead of picking a random node, we select nodes in proportion to a resource that we hope that nobody can monopolize: the computing power. In this way the result is an approximation of a random selection. In other systems, the selection is done in proportion to the currency ownership (proof-of-stake). We will see that in details later.

In order to add a block, the node that proposes it has to find a number: a nonce. This nonce concatenated with the hash of the previous block and the transactions Merkle Tree hash, must have an hash that falls into a small target space. The space is small in relation to the entire output space of the hash function.

H(NONCE | hash_prev_block | hash_transactions) ∈ {target_set}

Problem Difficulty

The idea is that it must be moderately difficult to find a nonce that satisfies this required property, which is that hashing the whole block together including that nonce is going to result in a particular type of output. If the hash function is secure, then the only way to succeed in solving this hash puzzle is to try enough nonces one by one until one gets lucky.

For example, if the target space was just 1% of the overall output space, it would be necessary to try about 100 nonces before one gets lucky. The real target space is much smaller, so the attempt to find a correct hash will be many more.

So, instead of needing somebody to pick a random node, the nodes are independently competing to solve these hash puzzles. Once in a while, one of them will find a random nonce that satisfies this property and will have the right to propose the next block. So the system is completely decentralized.

Proof-of-Work Properties

The proof-of-work function of an hash puzzle must be:

1. difficult to compute. For example nowadays it is necessary to compute about 1020 hashes to be able to insert a new block. So the size of the target space is only around 1/1020 of the output space of the hash function. It is almost impossible to solve this problem with a common laptop. So only some nodes of the network with high computing power actively compete in the block creation process. These blocks are called miners.
2. the difficulty is parameterizable. The target space is not fixed, but the BitCoin network automatically re-calculates the target every two weeks. This computation is done in such a way to maintain unchanged the average time between two consecutive blocks creation (10 minutes). So, if you have invested on a fixed amount of hardware, the rate at which you find blocks is actually dependent upon what other miners are doing. If the power of miners increase, you will have more work to do to be able to solve the problem. The probability that a miner is going to win the next block is equivalent to the fraction of global hash power that he controls. If blocks were to come very close together, then there would be a lot of inefficiency, and we would lose the optimization benefits of being able to put a lot of transactions.
3. It’s trivial to verify the new node has computed proof-of-work correctly. In fact, any other node can look at the block contents and verify that the output is less than the target computing a single hash. So no central authority is necessary to do the verification.

Proof-of-work and security

Thanks to the properties of this cost function and proof-of-work, it is possible to reformulate our security assumption.

So now, instead of saying that somehow the majority of nodes are honest, we can state that a lot of attacks on BitCoin are infeasible, if the majority of miners weighted by hash power are following the protocol.
In fact this competition for proposing the next block will automatically ensure that there is at least a 50% chance that the next block to be proposed at any point is coming from an honest node, instead of a malicious one.

Why solving hash puzzles is probabilistic?

Why is solving hash puzzles probabilistic? Because nobody can predict which nonce is going to result in solving the hash puzzle. The only way to do is to try nonces one by one, and hope that one succeeds.
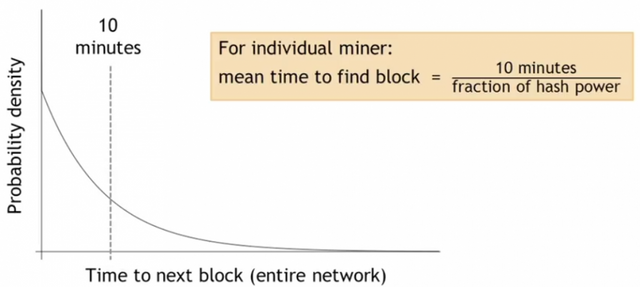
This process is called mathematically Bernoulli trials. The nodes try so many nonces that the discrete probability called Bernoulli trials can be well approximated by a Poisson continuous probability. The end result is that the distribution, the probability density function of the time to find the next block by any node is an exponential distribution.

It means that there is some small probability that if a block has been found now, the next block is going to be found very soon, or within a few seconds, or within a minute. And there is also some small probability that it will take a long time to find the next block.

If you're a single miner interested in how quickly you're finding blocks, this probability density function will have the same shape, but a different scale on the X-axis. For a specific miner, the mean time to find a block is 10 minutes divided by the fraction of hash power that he controls. So, if you have 0.1% of the total network hash power, you're gonna find blocks once every 10.000 minutes, which is several days. So, both the mean time between blocks creation and the time variance between blocks found by you will be very high.