Game Theory 102 - Blockchain and Cooperative Games
This post looks at how blockchain systems can improve our societies through an analysis based on "game theory".
"Games" and theory
A few months ago I wrote Game Theory 101 - Schelling point or "Why Steemit.com is important".
For those who are not familiar with "game theory", it is a branch of mathematics, more precisely the “mathematical models of strategic interactions between rational decision-makers”. Most if not all human interactions can be seen as "games" through the lens of this branch of mathematics.
One of the best books I've read on this topic is "The evolution of cooperation" by Robert Axelrod (pretty old book, I recommend you buy it if you can afford, but you can probably also find it as downloadable PDF).
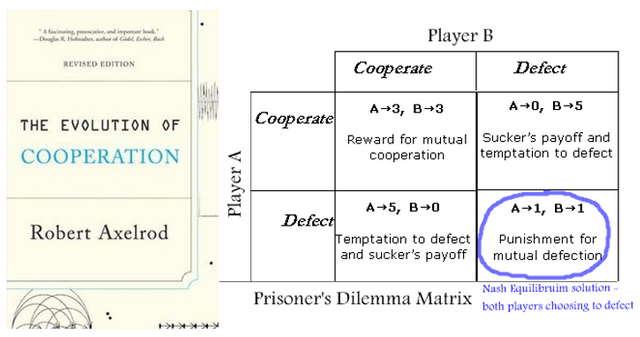
Table on the right - payout matrix in "Prisonner's dilemma" - from the "Lime 'n' Lemony" blog of Ashima, a lady I can easily picture blogging on Steemit
I do not intend to make this article into an introduction to game theory, enough saying that this is an absolutely fascinating and highly relevant field of study. If you are more of a "video" person than a "book" person, I recommend watching the YouTube videos on this topic from Systems Academy
Simplifying a bit, let's say there are two types of games, "competitive games" and "cooperative" games.
Competitive games involve interactions where the sum of pay-offs is constant and one player's win is another player's loss. Imagine dividing a pie in two or more parts: increasing the size of one player's part necessarily reduces the size of some other player's part.
In contrast, cooperative games arise where the total sum of pay-offs is not fixed but instead depends on the strategies chosen by the different players. To use the same analogy, depending on the choices of the playrs to total size of the pie can increase.
The majority of our real life interactions can be framed as "cooperative games", whereas "competitive games" are mostly to be found in sports and competitions.
As illustrated in the schematic below, when people cooperate, there's often an "added value", which is the difference between the actual result of their cooperation and the simple arithmetic sum of their separated efforts.
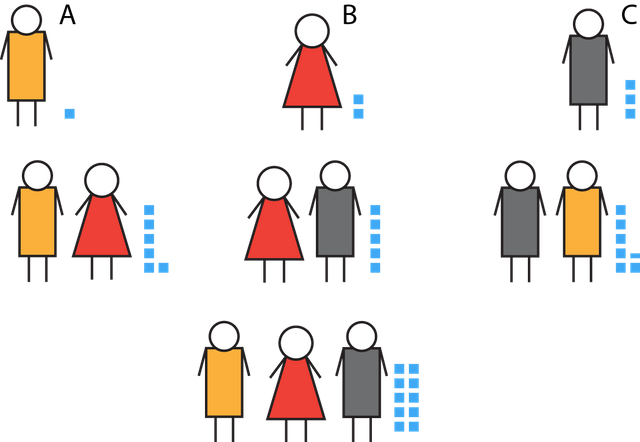
In this example, the output of the effort is measured in little blue squares. Person A working alone produces 1 unit, while during the same period person B working alone produces 2 units and person C produces 3 units.
You can notice that B and C working together produces no added value: the combined output is 2+3 = 5 units.
On the contrary, A and B working together produce 6 units rather than the sum of their individual outputs (1+2 = 3). A also displays synergy with C, as their combined efforts produce 6,5 units, or 2,5 more than the sum of their separate efforts.
Now look at the result of all three (A, B, and C) cooperating: their combined output is 10, or an added value of 4. Clearly, they should work together, right?
Well, not so fast ... The real question that all three are asking is: "how are we going to split the proceeds of our cooperation?" Imagine each one starts by getting what she would have produced on her own; how then to equitably split the added value of 4 units?
The importance of having a commonly accepted answer to this question from the outset cannot be underestimated. If any of A, B, or C fears that they might end up shortchanged, cooperation will be less effective or won't happen at all!
Found on the blog of Marcella Purnama, another blogger that we could have here on Steemit
The Aumann-Shapley value
It turns out the problem of fairly distributing the added value produced by cooperation is a mathematical problem which has been solved more than half a century ago by Lloyd Shapley. The solution concept he introduced has been called "the Shapley value".
The concept has been extended later to repeated games by Shapley with Robert Aumann in a book published in 1974: Values of non-atomic games
Blockchain as an Aumann-Shapley machine
Blockchain has been dubbed "the trust machine" since at least 2015. Yet more than 3 years after, I seldom meet people who truly understand what its implications are.
Most people still think of it as yet another fancy technology, like Cloud, IoT, AI and what have you, “so let's sell consulting gigs and brand new IT projects and systems under this new blockchain label".
Blockchain systems have several important capabilities:
- Transparency, which breaks information asymmetry.
- The ability to record pledges, facilitating coordination
- The built-in value-tracking token and associated transaction ledger, which facilitate calculation of the Shapley value.
Most (or almost all) businesses are built with "a moat" to help them protect their competitive advantage, and secretly dream of becoming monopolists and extracting the ensuing rent. Against this background, blockchains appear horribly disruptive, as they expose rents being extracted by incumbents.
Blockchains can support "open enterprises" or "cooperatives" where participants can pledge a contribution, their fellows can track that contribution and the blockchain can reward the contribution made in a fair manner. In "game theory" terms, "prisoner dilemmas" games become "stag hunt" games. In other terms, blockchain systems can support more and better coordination in "cooperative games".
Steem is the first example I know of such a blockchain eco-system, and Utopian is one of the most remarkable examples of such "open enterprises", governed not by a de jure contract but by social contract.

If you know what witnesses are and agree that people commited to keeping this blockchain ticking play an important role ...

(by simply clicking on the picture - thanks to SteemConnect)

Related posts
- Game Theory 101 - Schelling point or "Why Steemit.com is important"
- Blockchain revolution: Money and Credit
- Why Blockchain Is a Revolution
Blockchain, Crypto and Society
- What's Bitcoin's Value?
- Why NOT buying Bitcoin is completely irrational
- How to buy Bitcoin in the Eurozone - Comment acheter du Bitcoin dans la zone euro
- A New Hope
- Hack Your Life in 3 Easy Steps!
- The Holy Blockchain
- Crazy crypto evening
- Small worlds
- The Press needs to be Freed from the Tyranny of Money
- Immigrate to Romania!
- Blockchain in large organizations
- Blockchain revolution: the CIOs' dilemma
- The Heist: How Big Blue stole Blockchain!
- Blockchain Explored - why the industry loves IBM
- Blockchain and the End of the Western Civilization
- The Church of Bitcoin
- The Ressolid Project
- De l'argent (Steemit en français, la suite)
Other posts you might enjoy:
Blockchain and Europe
- Incentive-based regulation - Blockchain opens up a new era of European integration
- EU-citizens-blockchain-in-a-box
- Europe, I love you! - Europe, je t'aime!
- The Blockchain Competence Center (BLKCC)
- European Financial Transparency Gateway
- Toward a pan-EU blockchain infrastructure
- Blockchain and Data Virtualisation
- Blockchain, Credentials and Connected Learning Conference
- Decentralized Learning: The Future of Student Mobility in Europe
- The "war for [steem] blockchain talent" has been engaged - Fujitsu allies with EC
- Blockchain4EU
- Poker Champion Tony G turns MEP Blockchain Champion!
- Virtual Currencies - an EP report July 2018 - Part 1
- Central Bank Digital Currencies - Part 2 of the "Virtual Currencies" EP report of July 2018
- Blockchain taming the Dragon of Corruption
- Sovereign identity on blockchain
- Blockchain and GDPR - a Call to Arms!
Steem ecosystem
- How I learned to stop worrying and love the Bid Bots
- Help Yourself! (steemit for dummies)
- Steem crypto-economics
- Best way to Grow on Steemit
- Spammers gonna spam - focus on original content!
- Turn up the Heat! Steem Luxembourg
- The best time to publish is now
- Historic evening: first beer paid with SBD in Luxembourg (+ Fr)
- Steem $10Bln!
- Setting up a new Witness Node!
- Why would anyone burn a bear? - SteemFest 3
- Steemit and the Fractal Society
- Crypto-contradictions
- The Steemit adventure [2]
You might also want to check out
- my “lighthearted” account, @sorin.lite, perhaps you’ll like what you’ll see.
- the Ressolid account
- the Witness account, @lux-witness (and even approve it, perhaps)

Game Theory was designed as one of the main pillars in the Proof-of-Work consensus algorithm that made Bitcoin Possible.
Seeing as Blockchain is the by-product to give Bitcoin its immutability, it's only fitting that the application of Blockchain technologies can improve society via the application of Game Theory.
Good Read!
Thanks!
@sorin.cristescu Don’t you think this must be like;
A=1
B=2
C=3
A+B=1+2/2=1.5
B+C=2+3/2=2.5
A+C=1+3/2=2
A+B+C=1+2+3/3=2
Posted using Partiko iOS
If I understand well you'd split the added value evenly. A+B gives indeed an added value of 3 (total is 6). But B+C has an added value of 0: B produces 2 alone and C produces 3 alone and B+C produces exactly 5.
Anyway, splitting the added value half-half seems fair when there are only two participants but becomes problematic at A+B+C. The added value is 4 (1 of A + 2 of B + 3 of C + 4 of added value from cooperation= 10). A receives 4/3 = 1.33 on top of his 1, for a total of 2.33. But if A only works with B then it gets 1+1.5 = 2.5. So for A, it makes more sense to work only with B than with B and C, although the A+B+C combination produces more (10) than the (A+B) combination and C taken separately (6+3 = 9)
The Shapley calculation (which you find on Wikipedia) takes this into account in order to compensate A such as it's in his own interest to enter into the A+B+C combination
yes A+B+C produce bigger value at the total but C always gets lower value because of A in return
"Lower" with respect to ?... Each of them starts by receiving what they would have gotten working alone, so C will anyway always get at least 3. Whether he receives more than that and how much more depends on how successful he is at cooperating. For instance, with B, the team is not great as it produces 0 added value. With A, the total added value is 2.5 so C receives 1.25. For A+B+C, as long as C gets at least 1.26 (instead of 4/3=1.33) it will be in his own interest to work in the trio. That 0.07 allow A and B to go from 1.33 to 1.36-1.37 for instance. Still not 1.5 though, but a bit better
Thaks for the witness vote!
Game theory is incredibly interesting. Prisoner's dilemma is one of the most discussed games. Prisoner's dilemma is a bigger problem for one-off games. Repeated games are mostly to reach some form of cooperation to avoid perpetual defecting.
Steem bid bots are a perfect example of prisoner's dilemma for both buyers and sellers. Lucky for us it is a repeated game with infinite rounds.
In reality there are games within games which involve competition and cooperation. I think many focus on competition but cooperation has great potential especially for smaller participants.
This is a good theory, however, when I see "the rational" decision makers then I think that it would be possible to discuss it as well... for me, this statement about rationality is similar to communism where they foresee that all people are good...
You don't need to - blockchain enables transparency, you enter in a cooperation with who you trust
Nowadays the situation that we are going through in Venezuela is critical economically, politically, and even socially and you all know it, the government is a huge brazenness, people no longer have hope, and only take a decision that is to emigrate to another country. . These months have been getting worse, with your vote you will help a group of people you will be very grateful AYUDAME CON TU VOTO EN ESTE COMENTARIO se te agradecera mucho
How about investing unlimited amount on Steem, is this not a monopoly?
Maybe we could minimize or say put some tolerance on investments, a limit on amount to invest on Steem in order in some way to reduce the gap or make some a little bit of balance on the investments between the few huge amount investors and the many little investors.
My words are quite rambling, I hope you understand what I mean.
Yes, I think I understand. Steem is a "plutocracy". Far from perfect when compared to our current democratic society but the human society has evolved 7000 to reach this state. Blockchain community have evolved from "absolute monarchies" to include some degree of power dispersion over only 3 years, a pretty good result.
I recommend you read this post: Why Blockchain is a Revolution
Spotting this post made me join steemit. I lived that book and your post is really informative. More of this!
Thanks, enjoy the freedom :)
Still trying to understand the concept being of steemit .
In past 4 days i concluded that 70% are bots rest 30% are giants who just eats up new commers ;D
Nobody eats up anybody. If you like to create content, whether prose, poetry, photography, art, you are free to do so and post here.
The worst that can happen is that you get less engagement than you hoped for.
If you came for the money you'll notice that you make a lot less than "the giants". Just like in the real world, no reason to expect steemit to be somehow "magic"
What is with all these bots?
I've explained in these posts:
Thanks!
I guess Steemit has yet to perfect their security algorithms.
the bots are a kind of advertising mechanism - you pay for visibility. Please read this article
Help Yourself! (steemit for dummies)
Hey there !
Very well made posts (replying here for your whole blog), very inspiring for me as I try myself to write articles. I recently made an article about an idea of dApps on the steem blockchain and I'm satisfied but I can't see by myself how I could have done better..
I let you the link if you have the time ;-)
Continue your very well written blog, it's a pleasure to read it !