In this case,we just use stander python math lib to implement linear reg.

First,The line for a simple linear regression model can be written as:

y=b1*x+b0

1,calculate the mean and variance（均值与方差）：

mean=lambda value:sum(value)/int(len(value))

variance=lambda value,mean:sum([(x-mean)**2 for x in value])

1. Calculate Covariance（协方差）：

def covariance(x,mean_x,y,mean_y):
covar=0.0
for i in range(len(x)):
covar+=(x[i]-mean_x)*(y[i]-mean_y)
return covar

3,make prediction:
The simple linear regression model is a line defined by coefficients estimated from training data.

预测

def prediction(train,test):
predictions=[]
b0,b1=coeffients(train)
for row in test:
yhat=b0+b1*row[0]
predictions.append(yhat)
return predictions

Final,calculate root mean square error and evaluate:

计算平方根误差

def root_mean_square_error(actual,predicted):
sum_error=0.0
for i in range(len(actual)):
prediction_error=predicted[i]-actual[i]
sum_error+=(prediction_error**2)
mean_error=sum_error/float(len(actual))
return math.sqrt(mean_error)

评估训练集上的回归算法

def evaluate_algorithm(dataset,algorithm):
test_set=[]
for row in dataset:
row_copy=list(row)
row_copy[-1]=None
test_set.append(row_copy)
predicted=algorithm(dataset,test_set)
print(predicted)
actual=[row[-1] for row in dataset]
error=root_mean_square_error(actual,predicted)
return error

All code are here:

import math
import matplotlib.pyplot as plt
data={'X':[108,19,13,124,40,57,23,14,45,10,5,48,11,23,7,2,24,6,3,23,6,9,9,3,29,7,4,20,7,4,0,25,6,5,22,11,61,12,4,16,13,60,41,37,55,41,11,27,8,3,17,13,13,15,8,29,30,24,9,31,14,53,26]
,'Y':[392.5,46.2,15.7,422.2,119.4,170.9,56.9,77.5,214,65.3,20.9,248.1,23.5,39.6,48.8,6.6,134.9,50.9,4.4,113,14.8,48.7,52.1,13.2,103.9,77.5,11.8,98.1,27.9,38.1,0,69.2,14.6,40.3,161.5,57.2,217.6,58.1,12.6,59.6,89.9,202.4,181.3,152.8,162.8,73.4,21.3,92.6,76.1,39.9,142.1,93,31.9,32.1,55.6,133.3,194.5,137.9,87.4,209.8,95.5,244.6,187.5]}

求均值和方差

mean=lambda value:sum(value)/int(len(value))
variance=lambda value,mean:sum([(x-mean)**2 for x in value])

协方差

def covariance(x,mean_x,y,mean_y):
covar=0.0
for i in range(len(x)):
covar+=(x[i]-mean_x)*(y[i]-mean_y)
return covar

计算系数

def coeffients(dataset):
x=[row[0] for row in dataset]
y=[col[1] for col in dataset]
x_mean,y_mean=mean(x),mean(y)
b1=covariance(x,x_mean,y,y_mean)/variance(x,x_mean)
b0=y_mean-b1*x_mean
return [b0,b1]

预测

def prediction(train,test):
predictions=[]
b0,b1=coeffients(train)
for row in test:
yhat=b0+b1*row[0]
predictions.append(yhat)
return predictions

计算平方根误差

def root_mean_square_error(actual,predicted):
sum_error=0.0
for i in range(len(actual)):
prediction_error=predicted[i]-actual[i]
sum_error+=(prediction_error**2)
mean_error=sum_error/float(len(actual))
return math.sqrt(mean_error)

评估训练集上的回归算法

def evaluate_algorithm(dataset,algorithm):
test_set=[]
for row in dataset:
row_copy=list(row)
row_copy[-1]=None
test_set.append(row_copy)
predicted=algorithm(dataset,test_set)
print(predicted)
actual=[row[-1] for row in dataset]
error=root_mean_square_error(actual,predicted)
return error

result=evaluate_algorithm([data['X'],data['Y']],prediction)
print(result)
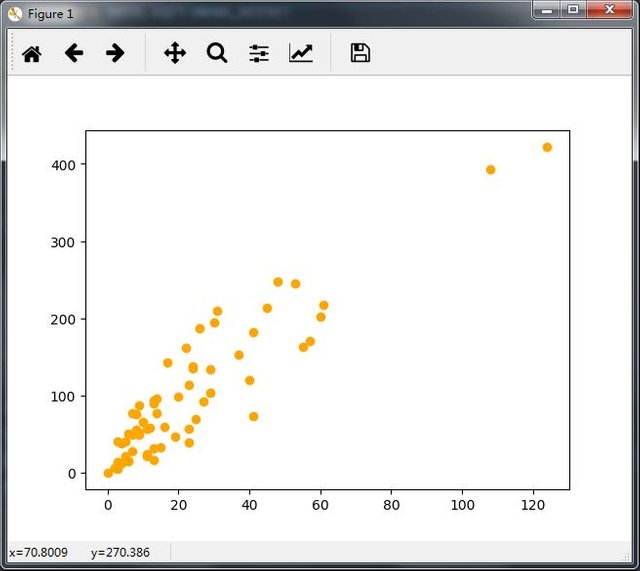
plt.scatter(data['X'],data['Y'],color='orange')
plt.show()