Factorización, Productos Notables y Simplificación - GMath


Factorización y Productos Notables
La Factorización, es escribir una expresión algebraica como un producto de factores, una suma, una resta, una matriz, un polinomio, etc, tal que éstos factores sean primitivos entre si dos a dos, si es que los hubiese. Los términos de factorización, simplificación y productos notables, están estrechamente relacionados entre si.
A continuación presentaremos algunos de los casos más comunes que nos podemos encontrar:
- Factor Común:

- Producto Notable al Cuadrado, o Factorización de una ecuación con términos cuadráticos:
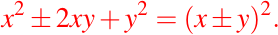
- Factorización de diferencias de cuadrados o Producto de binomios con distinto signo:
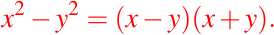
- Producto notable al cubo o Factorización de una ecuación con términos al cubo:
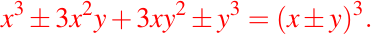
- Factorización de diferencias o sumas de términos al cubo:

- Factorización de ecuación de segundo grado ó desarrollo de producto de dos binomios:
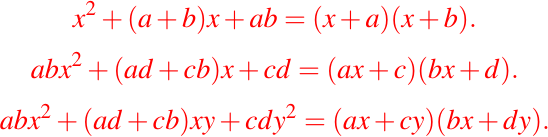
Simplificación
Para simplificar o reducir una expresión algebraica a sus términos más simples, basta con descomponer tanto el numerador y denominador de un cociente, en sus factores primos y luego dividir numerador y denominador por el producto de sus factores comunes basándose en el principio: “el valor de una fracción no cambia si el numerador y el denominador se multiplican o dividen por la misma cantidad distinta de cero”.
Es por ello, que es muy importante conocer y manejar el punto anterior muy bien, o digamos que casi perfectamente.
División de Polinomios
Para dividir dos polinomios, debemos seguir el siguiente algoritmo:
- Se ordenan ambos en el mismo sentido descendente o ascendente por las potencias de una misma variable.
- Se divide el primer término del dividendo por el primer término del divisor y este cociente será el primer término del cociente.
- Se multiplica este término por todo el divisor y se escribe el resultado por debajo de los términos semejantes correspondientes del dividendo.
- Se resta del dividendo.
- Utilizando los términos de primer resto como nuevo dividendo, se repiten los pasos 2, 3, y 4.
- Se continua del mismo modo hasta que no queden términos en dividendo para bajarlo. Si el último resto es cero, la división es completa y exacta.
- Si queda un resto la división es inexacta, no existe ningún polinomio que multiplicando por el divisor reproduzca el dividendo, pero el cociente completo, será el polinomio formado por todos los términos hallados en el cociente, más la fracción cuyo denominador será el resto, correspondiente al último término del cociente y por denominador el divisor.
Al dividir polinomios, lo que queremos es determinar el cociente y resto y escribir el resultado de la siguiente manera:
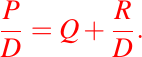
donde P es el dividendo, D el divisor, Q el cociente y R el resto de la división de dos polinomios.

Queridos amigos y lectores, espero hayan disfrutado leyendo esta serie de 10 publicaciones, donde tratamos algunos temas de importancia de Matemáticas Básicas o Pre-Universitaria, los espero en la próxima serie de contenido de matemáticas donde trataremos algunos temas con un nivel más avanzado, donde trataremos de manera similar a esta serie. Espero que esto pueda servir de apoyo a ustedes, hijos, nietos, sobrinos o amigos que quieran aprender un poco mas del maravilloso mundo de las matemáticas. No olviden dejar sus comentarios. Saludos y nos leemos pronto.
Si desean consultar un poco más del tema pueden usar las siguientes referencias.
- Baldor, J. Aurelio. Álgebra Elemental. Cultural Centroamericana, 1972.
- Baldor, J. Aurelio. Aritmética. Cultural Centroamericana, 1978.
También los invito a leer mis otras publicaciones que puedan ser de su interés:
Todas las imágenes y ecuaciones fueron creadas y editadas por @abdulmath con  , y GIMP.
, y GIMP.

Imagen elaborada por @abdulmath, diseñadas y editada con Karbon y GIMP.
Este tema de simplificaciones, me dio mucho dolor de cabeza, ojalá me hubiese podido encontrar en mis tiempos a un profesor como usted, que con detalle prepara sus temas. Muy bien y claro. Lo compartiré con mis nietos.
Hola @rmartinezpoeta, que bueno que le hayan gustado mis publicaciones, esta semana subiré un poco de nivel, pero seguiré tocando temas básicos, y prácticos. Saludos y un abrazo.
wow, excelente información. me gusto lo fácil que es entenderlo. Debes ser un gran profesor.
Hola @anaiscarolina03, gracias por tu comentario, y que hayas visitado mi blog. Te invito a leer mis otras publicaciones y evaluarlas. Espero que mis estudiantes digan lo mismo, jejejejeje. Saludos y un abrazo.
Aprendiendo con usted profe. Gracias por compartir.
Hola @carmenmdm, gracias, Saludos y un abrazo.
Buen trabajo @abdulmath.
Hola @anmilnet, gracias, seguimos trabajando, Saludos y un abrazo.
Wow que lástima no haberte conocido en el instituto, me hubieras facilitado mucho los estudios jajaja. Saludos
Hola @jackass, que bueno leer esas palabras. Anima a seguir remando en la misma dirección. Saludos y un abrazo.
Opino igual que muchos, debí de conocerlo hace unos años y que fuese mi profesor jajaja
Hola @paos, gracias, que bueno saber que lo estoy intentando hacer bien. Saludos y un abrazo.
Saludos amigo @abdulmath, excelente trabajo, mu bueno.
Un Abrazo
Muchisismas gracias por tus palabras. Saludos hermano