An Introduction to Time Complexity and Big O Notation

According to Wikipedia,

In computer science, the time complexity is the computational complexity that describes the amount of time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by the algorithm, supposing that each elementary operation takes a fixed amount of time to perform. Thus, the amount of time taken and the number of elementary operations performed by the algorithm are taken to differ at most by a constant factor.

Since an algorithm's running time may vary among different inputs of the same size, one commonly considers the worst-case time complexity, which is the maximum amount of time required for inputs of a given size. Less common, and usually specified explicitly, is the average-case complexity, which is the average of the time taken on inputs of a given size (this makes sense because there are only a finite number of possible inputs of a given size). In both cases, the time complexity is generally expressed as a function of the size of the input. Since this function is generally difficult to compute exactly, and the running time for small inputs is usually not consequential, one commonly focuses on the behavior of the complexity when the input size increases—that is, the asymptotic behavior of the complexity. Therefore, the time complexity is commonly expressed using big O notation, typically O(n), O(n log n), O(2^n), etc. where n is the input size in units of bits needed to represent the input.[1]

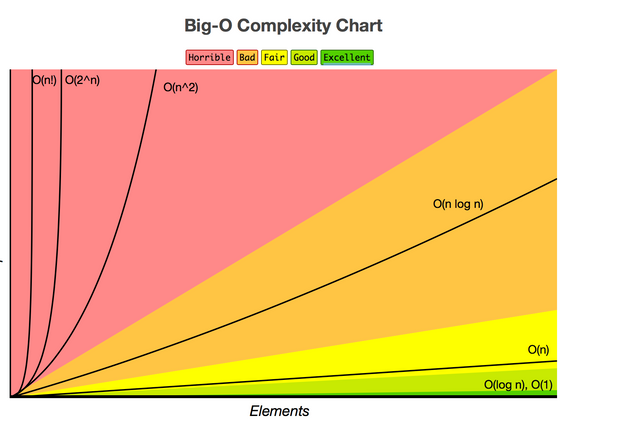
O(N), is referred to as “order of growth N”, “O of N” , “Order N”

Big O notation, otherwise known as algorithmic efficiency, is a way to describe the complexity or performance of a given algorithm. Another way to consider Big O is how time scales with respect to some input variables In computer science, we are interested in how fast an algorithm is, or how fast a certain set of instructions is.

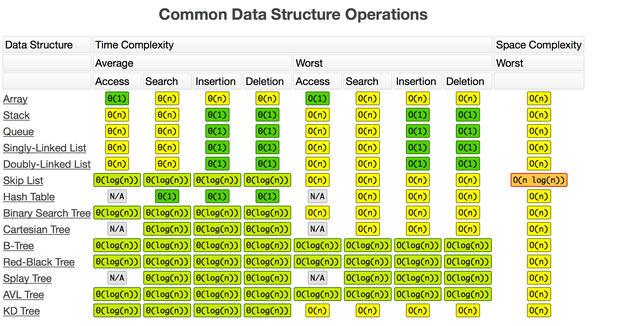
Generally we consider how fast an algorithm is in the case it takes a large set of inputs. If you need to sort five dogs in order of age, the algorithm speed barely matters; but if you need to sort ten billion dogs in order of age, then choosing the wrong algorithm can mean the difference between a runtime of a few minutes and a few days.

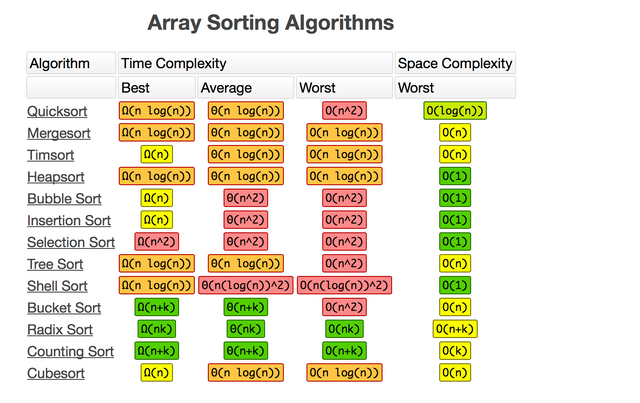
• Best case complexity tells us the complexity when we are very lucky. It represents the fewest number of steps that an algorithm can take. For Alice’s guessing game, the best case occurs when she is thinking of the number 1 and Bob only needs to make one guess. In general, best case complexity is not very useful as a complexity measure. We would not want to choose an algorithm due to its best case complexity and then hope we get lucky in terms of the input conditions.
• Average case complexity represents the average number of steps required, con- sidering all possible inputs. In the guessing game case this is not dif􏰁icult to deter- mine: if all of the numbers between 1 and 1,000 are equally likely to occur, then on average it will require (1 + 1,000) /2 = 500.5 guesses to guess a number. Average case complexity analysis can be useful but it is often dif􏰁icult to de􏰁ine for a speci􏰁ic algorithm.
• Worst case complexity represents the highest number of steps that an algo- rithm would require. If Alice is thinking of the number 1,000 then Bob will need to make 1,000 guesses.

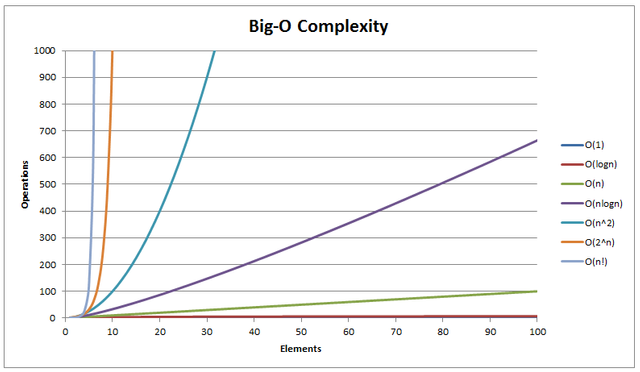
Before continuing with a discussion of the time efficiency of algorithms we should point out that quite often time efficiency and space efficiency are interrelated, and trade-offs between time and space efficiency can be made. Consider, for example, the problem of sorting a deck of cards numbered 1–300. Suppose you are sitting on a bus with these cards and have to sort them while holding them in your hands. You will spend a lot of time shuffling through the cards, and you will most likely need to look at each card many times. Alternately, imagine trying to sort the same set of cards if you are standing in front of a table large enough to hold all 300 of them. In this situation you can look at each card just once and place it in its correct spot on the table. The extra space afforded by the table allows for a more time-efficient sorting algorithm.

How do programmers compare the time ef􏰁iciency of two algorithms? The f􏰁irst approach that comes to mind is simply to code the algorithms and then compare the execution times after running the two programs. The one with the shorter execution time is clearly the better algorithm. Or is it? Using this technique, we really can determine only that program A is more ef􏰁icient than program B on a particular computer at a particular time using a particular set of input data. Execution times are specific to a particular computer, because different computers run at different speeds. Sometimes they are dependent on what else the computer is doing in the background. For example, if the Java run-time engine is performing garbage collection, it can affect the execution time of the program. Coding style and input conditions can also effect the time of a running program. A standard technique, and the one we use in this text, is to isolate a particular operation fundamental to the algorithm and count the number of times that this operation is performed. When selecting which operation to count, we want to be sure to select an operation that is executed at least as many times as any other operation during the course of the algorithm.[2]

Some Useful Videos

Links

http://bigocheatsheet.com (images taken from here)

https://en.wikipedia.org/wiki/Time_complexity[1]

https://cdn.preterhuman.net/texts/math/Data_Structure_And_Algorithms/Object-Oriented%20Data%20Structures%20Using%20Java%20-%20Nell%20Dale.pdf[2]