[Answer and winners] Mathematics × Programming Competition #2 [公佈得獎名單] 數學 × 程式編寫比賽 (第二回)
Mathematics × Programming Competition #2
Announcement of the Answer and Winners
Announcement of the Answer and Winners
數學 × 程式編寫比賽 (第二回)
答案及得獎名單公佈
答案及得獎名單公佈
Question 問題
A regular 2017999-sided polygon is drawn on a rectangular coordinate plane, with (0,0) as its center and the distance between any vertex to the center is 1. It is given that one of the vertices is (1,0). Find the sum of x- and y-coordinates of all the other 2017998 vertices.
在直角坐標系統上,我們以(0,0)為中心畫出一個正2017999邊形。它中心與任意一個頂點的距離為1。已知其中一個頂點為 (1,0),求其他所有2017998個頂點的x坐標及y坐標之和。
Photo source: https://ds055uzetaobb.cloudfront.net/
Answer 答案: -1
Mathematical approach 數學解法
Let the number of vertices be N. First of all we should note that the nth vertex starting from (1,0) in the anti-clockwise direction has the coordinates ( cos (2πn/N) , sin (2πn/N) ), where n is from 0 to N-1.
It is easy to observe the summation of y-coordinates is 0, as the polygon is symmetric about x-axis regardless of the value of N.
However the polygon is only symmetric about the y-axis if N is even. Note that N is odd in this case, so we cannot conclude the summation of x-coordinates is 0 right away. (A lot of proofs submitted claimed that summation of x-coordinates = 0 because of symmetry, which is wrong!)
What if we put the coordinates on a complex plane instead? Then the nth vertex now can be written as cos (2πn/N) + i sin (2πn/N). By the De Moivre's formula1, we know that each of these vertices satisfies the equation zN = 1. The sum of roots of this equation is 0, which means both the sum of real part and sum of imaginary part of the vertices are 0. Put it in another way, we have and
.
Taking away the point (1,0), our answer should be -1. Actually the value of N does not matter!
1 De Moivre's formula:
設N為頂點數目。將圖形置於複數平面,第n個頂點可寫成cos (2πn/N) + i sin (2πn/N)。由 De Moivre's formula 可知每個頂點均附合方程zN = 1。此方程的根之和為0,即實數和虛數部分均為0。因此可得
及
。除去頂點(1,0),答案為-1。事實上N的數值並不重要!
Programming approach 編程解法
JavaScript:
var sum = 0;
for (var i = 1; i < 2017999; i++){
sum = sum + Math.sin(i / 2017999 * 2 * Math.PI) + Math.cos(i / 2017999 * 2 * Math.PI);
}
console.log(sum);
Output: [a number very close to -1, due to rounding errors]
輸出: [非常接近-1的數字,其誤差是由於捨入誤差。]
The above JavaScript snippet has been reviewed by @adnanrahic. You can visit his blog to learn JavaScript!
以上JavaScript程式經由@adnanrahic檢閱,你可以按以下連結學習一下JavaScript!
The JavaScript Journey 1 - Values
The JavaScript Journey 2 - Arithmetic and Operators
The JavaScript Journey #3 - Logical Operators
The JavaScript Journey #4 - Special Values & Precise Comparisons
Winners 得獎者
In 24 hours' time, we have received 19 responses! Thank you for all your participation!
在短短24小時的比賽時間,我們收到了19名參賽者的答案! 感謝大家的熱烈支持!
In the following list, the participants highlighted in yellow have won the first prize, while those highlighted in orange won the second prize! According to the rules, only the SBD payout of the announcement posts will be used as the prize pool, but unfortunately the amount is only several SBD. Nevertheless, I have decided to increase the prize pool to 20 SBD, using part of the payout from the question post!
下表以黃色標示者贏得第一名,而橙色者則贏得二獎。根據規則,只有預告帖的SBD金額方會作為獎池,但今次預告帖的SBD金額只有數SBD。不過我決定將獎池調升至20 SBD!
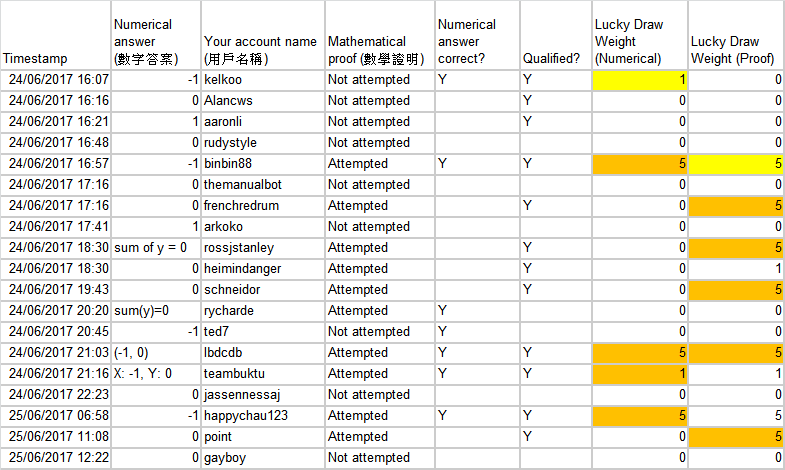
Congrats to @kelkoo and @binbin88 for being the first ones to submit a valid numerical answer and mathematical proof respectively, thus getting the 1st prizes!
In particular, @kelkoo has won the first prize for 2 consecutive competitions already! Great job!
恭喜 @kelkoo 和 @binbin88 分別奪得數字答案及數學證明的第一名!
而@kelkoo已第二次奪得第一名,表現實在驚人!
However, as you may notice in the table above, there are participants who answered the question correctly, but they didn't upvote both the announcement post and question posts, so they become ineligible for the prizes :( Make sure you read the rules carefully and hope that you can win next time! :)
然而有部分參賽者因未upvote預告帖,所以被取消資格。記得下次要清楚閱讀規則啊! 下表為派彩名單:
The winners and prizes have been tabulated below:
| Winner | Prize | SBD |
|---|---|---|
| @kelkoo | Numerical answer: first prize | 5 |
| @binbin88 | Numerical answer: second prize | 1 |
| @lbdcdb | Numerical answer: second prize | 1 |
| @teambuktu | Numerical answer: second prize | 1 |
| @happychau123 | Numerical answer: second prize | 1 |
| @binbin88 | Mathematical proof: first prize | 5 |
| @frenchredrum | Mathematical proof: second prize | 1 |
| @rossjstanley | Mathematical proof: second prize | 1 |
| @schneidor | Mathematical proof: second prize | 1 |
| @lbdcdb | Mathematical proof: second prize | 1 |
| @point | Mathematical proof: second prize | 1 |
We have one second prize for numerical answers not given out, since there are not sufficient qualified winners. SBD has been deposited into your wallet already :) Hope to see you in the next competition!
由於合資格的參賽者不足,是此比賽尚有一名數字答案二獎未被派發。SBD已派發予各位,希望下一次比賽再見到大家!
Upvote, resteem and follow me at @kenchung if you like my posts!
Thx for the contest :)
It was fun indeed ~
you are welcome bro :)
Oops... all the "other" 2017998 vertices.
All is 0
Other is -1
;D
@kenchung Thanks for a fun contest.
haha careless mistake ;) a lot of people answered 0 actually lol
Next time, I'll have to resteem. Did not read the rules careful enough, I guess :) I'm looking forward to your next competition!
ye haha resteem will earn you a much higher chance ;) see you in the next competition!
OK, this is a good one. I couldn't systemmatically list out my proof but at least I thought that it should be -1. Next time I will put in my answer anyway. Thank you for setting this contest up. A really good one! Enjoy it very much!
Sure, thanks for your support bro!
Bro you are great! My maths is suck... just support :)
haha nvm, you can still submit a wild guess, maybe you can get it correct! :)
Great job @kenchung! I'm very proud to be part of your awesome contests. :)
I am very honored to have you as my adviser! :)
期待下一次的比賽!xD
多謝支持 :D
不错的活动
再接再厉
謝謝啊,下一次你們也過來玩玩吧! :)
玩不转啊,脑袋早已秀逗了,哈哈哈哈
哈哈
預告一下,下一次主題會是比較亞洲風一點,玩不轉也過來湊湊熱鬧吧 :)
Congratulations! This post has been upvoted from the communal account, @minnowsupport, by kenchung from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, theprophet0, and someguy123. The goal is to help Steemit grow by supporting Minnows and creating a social network. Please find us in the Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.
If you like what we're doing please upvote this comment so we can continue to build the community account that's supporting all members.
Thank you sir~