RE: Is Monero’s (or All) Anonymity Broken?
As a prerequisite for understanding, my blog was lacking a layman’s introduction on Cryptonote’s ring signatures:
I will expound a little bit on the linked introduction above.
Cryptonote’s “one-time” ring signatures enable the signer of a transaction to group his public key with his choice of the public keys of other UTXO (unspent transaction outputs) on the blockchain.
(Tangentially note all transaction outputs are forever “unspent” because it is anonymous as to when they were spent, unless anonymity is unmasked as this blog posits; thus there is a claim that we should not name these UTXO and instead name them TXO)
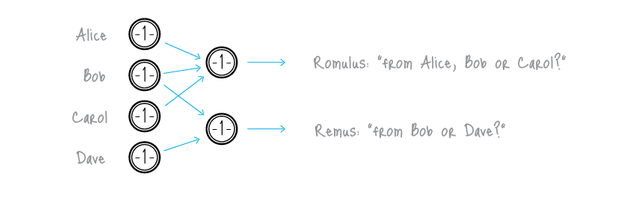
The number of public keys grouped is called the “number of mixins” or “mixin level”.
The signature is constructed in a mathematical way such that it proves the signer (his public key) is always associated with a certain generated “id” number I which is named the “key image” (no matter which public keys other than his own he chooses for the grouping), but this generated number does not enable anyone to know which of the public keys in the grouping is the signer. When they say the ring signature is “traceable” or “one-time” , they mean this generated “id” number, not the actual correlation of which signer.
Thus the validator of the blockchain can prevent the each signer of a transaction output from double-spending, because the blockchain stores the generated numbers and so if the signer attempts to spend again, there will be duplicate generated number already on the blockchain. In that way, the actual signer of each transaction is obscured in a grouping, yet the double-spend prevention feature of blockchains is maintained. This was quite genius and exciting when it was first released, but my blog posits how it can be deanonymized.
Note the generated number is derived from the public key of the signer in such a way that it is not tractable to reverse the derivation and determine who was the signer. This however only holds true if ECC (elliptic curve cryptography) and cryptographic properties of the chosen hash function remain intractable to crack.
I will not attempt to explain the math here. Someday perhaps I or someone will write a Cryptonote for Dummies blog on the math. It is actually quite interesting and if you understood math in high school then this can be explained to you at least a high level overview of the algebra.
Edit: the reason the image near the top has values of 1 on the coins is because Cryptonote required equal denominations for all UTXO in the ring mix set because the token values were not obscured. Monero’s RingCT upgrades Cryptonote adding homomorphic encryption of values.
Thanks for the clarification - the mists are clearing a little for me!