The Diffie-Hellman Protocol

This problem was one of the most important problems of the XX century. Before it was solved, people had to convey keys on a sheet of paper as during the Second World War. In 1976 breakthrough happened when an American cryptographer Whitfield Diffie together with his colleague, professor of Stanford University, Martin Hellman published key exchange scheme which later became known as the Diffie-Hellman protocol. Actually, neither Alice nor Bob doesn't transmit a secret key at all, but the key is generated on both sides just by the simple mathematical trick. This absolutely brilliant and simple solution made a real revolution in the world of encryption and launched a whole direction in cryptography called asymmetric cryptography (or public-key cryptography). So how can Alice and Bob get the same keys without passing them to each other?

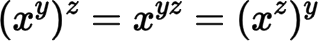
This expression is also valid for modular arithmetic which is the base for all cryptography schemes today. So you have to be familiar enough with this branch of math to understand how most of the ciphers work. To get the same key on both sides:

• Alice & Bob choose modulo m and exponent base g. This data is public, i.e. open to everyone and it won't compromise the key.
• Alice takes a random giant number a and doesn't show it to anyone. This is her secret key but not the one which will be used to sign messages.
• Alice calculates  (see modular arithmetics) and sends this number to Bob. She can reveal A to any person (it's a kind of public key).

Knowing the numbers a, g and m, it is easy for the computer to calculate A (for example, by the algorithm of Repeated squaring). But knowing A, g, and m, it is almost impossible (in a reasonable time), even for the fastest computer in the world, to calculate a. But in order for this to become impossible, it is necessary to select sufficiently large numbers (more than 100 characters). Otherwise, the computer can quickly look through all possible choices and crack the secret number.

It is known from school math that the inverse function for exponentiation is the logarithm. It seems not so difficult to calculate the logarithm 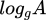, right? After all, even calculators can take logarithms of sufficiently large numbers. Not a hundred digits, of course, but computers are million times faster. he problem lies in the fact that the set of real numbers is continuous, and the logarithms are considered with a certain degree of approximation. However, in modular arithmetic, we use integers, which makes it impossible to approximate the calculation of the logarithm. This problem is called the discrete logarithm problem.

By the way, every asymmetric cryptography method uses functions that are easily computed in one direction and extremely difficult to compute in reverse (see Trapdoor functions or One-way functions with a hidden path). For example, the RSA algorithm uses the multiplication of two prime numbers, which is very easy to do, but the reverse operation - factorization - is extremely difficult to execute. And the Diffie-Hellman algorithm, as we saw previously, uses exponentiation in one direction (easy) and logarithms in the opposite direction (hard). A third well-known example is elliptical curves, which are actively used in modern protocols.

Now, continue with the keys:

• Bob, just like Alice did, takes a random giant number b and doesn't show it to anyone. This is his secret key but not the one which will be used to sign messages.
• Again, as Alice did, Bob calculates 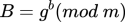 and sends this number to Alice (it's his public key).
• Having obtained the number A from Alice, Bob calculates .
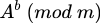• Having obtained the number B from Bob, Alice calculates .
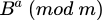• Using the property of exponentiation mentioned at the beginning of the article, we obtain

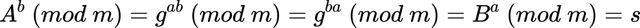
Voila! The magic of mathematics has done its work, and now both sides have the secret key s (without passing any secret information), which can encrypt further correspondence.

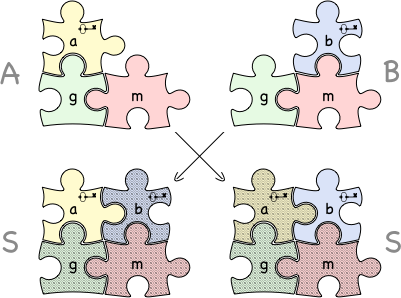
To consolidate all the previously written, we can go through all the steps using small numbers that are convenient for counting. In real systems this never happens, because extremely large numbers and very carefully selected inputs m and g are used since there are already ways to quickly find a and b from public data for certain m and g. For convenience, we will merge several steps into one.

1. Let m = 11, g = 2, a = 5, b = 3
2. 
3. 
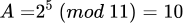
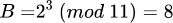
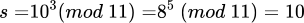4.  (the secret key)

This was a simple and elegant way to produce a common secret key that came to Diffie and Hellman bright minds when they were working on the concept of public-key cryptography in Stanford offices in the distant year of 1976.