WARNUNG

Dieser Artikel ist eine Gefahr für Unwissenheit und könnte Ihren Horizont erweitern! Der Autor ist nicht verantwortlich für Kopfschmerzen, Verwirrung oder mentale Zusammenbrüche jeglicher Art. Durch lesen dieses Artikels stimmen Sie zu, dass Ihre Unwissenheit zu Schaden kommen könnte. Lesen auf eigene Gefahr.

Bild Quelle

Roadmap

"Die Unendlichkeit und noch viel weiter" ist eine Reihe von Artikeln, über die mathematischen Eigenschaften von Unendlichkeit und wie unsere Intuition über die Unendlichkeit häufig daneben liegen kann. In den späteren Teilen wird es recht mathematisch und wir werden nicht um ein paar Formeln herum kommen. Ich werde jedoch mein bestes geben die Artikel so verständlich wie möglich zu schreiben. Sie müssen nicht Mathematik studiert haben, um sie zu verstehen.

• Teil 1 - Einführung
• Teil 2 - Wieso unendlich plus eins nicht größer als unendlich ist
• Teil 3 - Gibt es größeres als unendlich?
• Teil 4 - Interessante Gedankenexperimente für die verregneten Nachmittage

Dies sind die bereits geplanten Teile der Artikelreihe. Es kann sein, dass diese Liste noch überarbeitet wird.

Die Unendlichkeit und ihre praktische Anwendung

Das Konzept der Unendlichkeit wird wohl kaum im alltäglichen Leben vorkommen, jedoch lauert es in der Mathematik, Physik oder Informatik hinter jeder Ecke, bereit den unvorbereiteten Studenten zu übertölpeln. Betrachtet man es von einer philosophischen Seite so spiegelt die Fähigkeit des Menschen, sich solch abstrakte Dinge wie Unendlichkeit vorstellen zu können, seinen Erfindungsgeist und seine Fähigkeit hinter die Fassade zu blicken wider.

Schließlich ist noch nichts wahrhaft unendliches entdeckt worden. Ein Kreis ist unendlich. Jedoch nur, wenn man zulässt dass der selbe Punkt mehrfach berücksichtigt wird. Nach einiger Zeit hat man den gesamten Kreis besucht und wird nichts neues mehr finden. Das Universum könnte unendlich sein. Die Frage nach der Unendlichkeit des Universums ist jedoch müßig, denn nach einer gewissen Strecke (nämlich dem Rande des beobachtbaren Universums) kann uns keinerlei Information (visuelle oder anderweitige) erreichen, da selbst das Licht sich mit endlicher Geschwindigkeit fortbewegt. Ja, selbst das schnellste was unser Universum zu bieten hat, weil nichts anders schneller sein kann, ist immer noch endlich schnell.¹

Doch was ist mit den kleinsten Teilen unseres Universums? Selbst mit einem magischen Mikroskop gibt eine Grenze der Genauigkeit. Ohne hier zu sehr ins Detail zu gehen, denn dieses Thema könnte einen eigenen Artikel füllen, schauen wir uns ganz kurz die Begründung hierfür an. Die Heisenbergsche Unschärferelation stellt fest, dass die Position und der Impuls (also die Richtung und Beschleunigung) eines Partikels nur bis zu einer gewissen Genauigkeit gemessen werden kann. Versucht man einen sehr kleinen Partikel zu messen, so benötigt man immer höhere Frequenzen elektromagnetischer Strahlen (sehr schnell jenseits des sichtbaren Lichts) je genauer man messen will. Das Problem hierbei ist jedoch, dass je höher die Frequenz desto höher die Energie und je höher die Energie desto mehr wird der Partikel von der Strahlung beeinflusst. Der Strahl schubst den Partikel förmlich von seiner Position, die es ja zu messen galt. Schlussendlich führt dies zu einem Gleichgewicht zwischen dem Fehler durch unpräzises Messen (zu niedrige Frequenz) und dem Fehler durch Schubsen des Partikels (zu hohe Frequenz).²

Bild Quelle

An dieser Stelle könnte man sich Fragen "Wieso beschäftigen wir uns dann überhaupt mit Unendlichkeit?". Wie bereits erwähnt taucht die Unendlichkeit häufig in der Mathematik auf. Sie ermöglicht es uns Theorien aufzustellen und letzten Endes auch eine Ganze Reihe von Dingen zu beweisen. Eine der essenziellen Theorien der Mathematik ist der Gödelsche Unvollständigkeitssatz, der aussagt dass nicht alles was auch wahr ist beweisbar ist; und umgekehrt nicht alles was unwahr ist lässt sich widerlegen. Die Argumentation hierfür basiert stark auf unterschiedlichen Arten von Unendlichkeit.³

Selbst wenn Sie, lieber Leser, keinen mathematischen Hintergrund haben, so könnte es sein dass sie dennoch etwas aus dieser Artikelreihe über Unendlichkeit mitnehmen können. Im vierten Teil dieser Reihe werden wir uns einige Gedankenexperimente anschauen, die unsere Gehirne dazu zwingen werden sich ein paar Windungen mehr zuzulegen.

Moment, war da gerade die Rede von "unterschiedlichen Arten von Unendlichkeit"? Ist unendlich denn noch nicht groß genug? Jetzt gibt es auch noch verschiedene Arten? Oh ja, unendlich ist nicht gleich unendlich. Tatsächlich gibt es unendlich viele Arten von Unendlichkeit, jede größer als die vorherige.⁴ Mehr hierzu jedoch erst in Teil 3.

Die Grundlagen

Bevor wir uns jedoch in den Kern des Themas stürzen können muss erst der Grundstein gelegt werden. Gehen wir also kurz über ein paar Grundlagen und die ersten paar Formeln.

Mengenlehre

Mengen sind in der Mathematik ungeordnete Anhäufungen von Elementen oder Symbolen, wobei jedes Element nur genau einmal in einer Menge vorkommen kann. Zur Erstellung von Mengen verwenden wir eine Liste der Elemente der Menge umschlossen von geschweiften Klammern. Für Namen von Mengen nehmen wir üblicher Weise Großbuchstaben. Elemente von Mengen können zwar jedes beliebige Symbol sein, wir werden uns jedoch zumeist auf Zahlen beschränken, da das die Sache um einiges leichter macht. Neben bloßen Mengen benötigen wir auch noch ein paar Operationen, die uns Mengen verändern lassen. Hier ist ein kleiner Überblick über die grundlegenden Notationen.

Jetzt, da wir die Notation geklärt haben können wir los legen und uns eine erste unendliche Menge vornehmen. Symbole, die noch nicht erklärt wurden, werden nachgereicht sobald sie verwendet werden.

Eine unendliche Menge

Wir sollten uns alle recht gut mit den natürlichen Zahlen auskennen. Schauen wir uns also an, was die Unendlichkeit bei den natürlichen Zahlen für eine Rolle einnimmt.

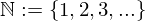
(Ob die Zahl Null in den natürlichen Zahlen enthalten ist oder nicht, ist reine Vereinbarunssache und kann sich von Paper zu Paper und Dozent zu Dozent ändern. Wir entscheiden uns dagegen die Null mit aufzunehmen.)

Die Menge der natürlichen Zahlen beinhaltet alle ganzen Zahlen von Eins bis Unendlich. Richtig? Dieser Satz ist ein recht gutes Beispiel weshalb Mathematiker immer diese seltsamen Zeichen und Symbole verwenden, wenn man doch genauso gut einfach sagen kann, was man will. Natürliche Sprache (wie Deutsch) ist unpräzise. Der Satz "Die Menge der natürlichen Zahlen beinhaltet alle ganzen Zahlen von Eins bis Unendlich." kann so interpretiert werden, dass man meinen könnte Unendlich ist ein Teil der natürlichen Zahlen. Allerdings ist dies nicht der Fall.

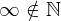
Folgt man seiner Intuition der natürlichen Zahlen, so lässt sich das recht leicht begründen. Die natürlichen Zahlen, sind alle Zahlen die wir zum Zählen verwenden. Man beginnt also "1, 2, 3, ..." und so weiter. Allerdings wird man, egal wie lange man zählt (selbst wenn man unendlich lange zählt) niemals zu dem Punkt kommen, an dem man "unendlich" sagt. Unendlich kann niemals erreicht werden, da es nicht Teil der natürlichen Zahlen ist.

Jetzt haben wir eine unendliche Menge mit der wir alle vertraut sind. Im nächsten Teil dieser Artikelreihe werden wir ein bisschen mit den natürlichen Zahlen spielen und schauen was wir so mit der Größe dieser Menge anstellen können.

Nächstes mal

Im nächsten Teil befassen wir uns mit der Frage warum unendlich plus eins nicht größer sondern gleich unendlich ist. Bleiben Sie also gespannt für einen der Teile der Mathematik, der Ihr Gehirn zu akrobatischen Leistungen zwingen wird.

Vielen Dank fürs Lesen. Sollten Sie Fragen haben oder sich kritisch über diesen Artikel äußern wollen, sind Sie herzlich dazu eingeladen, direkt hier unten in den Kommentaren. Ich werde mein bestes geben Ihre Fragen so schnell, vor allem aber so gut ich kann zu beantworten.

---

1. Das beobachtbare Universum - https://www.space.com/24073-how-big-is-the-universe.html
2. Heisenbergsche Unschärferelation - https://www.theguardian.com/science/2013/nov/10/what-is-heisenbergs-uncertainty-principle
3. Der Gödelsche Unvollständigkeitssatz - https://plato.stanford.edu/entries/goedel-incompleteness/
4. Arten von Unendlichkeit - https://thatsmaths.com/2014/07/31/degrees-of-infinity

---

Formeln erzeugt mit latex2png.