Die Unendlichkeit und noch viel weiter - Teil 2

Quelle
Roadmap
"Die Unendlichkeit und noch viel weiter" ist eine Reihe von Artikeln, über die mathematischen Eigenschaften von Unendlichkeit und wie unsere Intuition über die Unendlichkeit häufig daneben liegen kann. In den späteren Teilen wird es recht mathematisch und wir werden nicht um ein paar Formeln herum kommen. Ich werde jedoch mein bestes geben die Artikel so verständlich wie möglich zu schreiben. Sie müssen nicht Mathematik studiert haben, um sie zu verstehen.
- Teil 1 - Einführung
- Teil 2 - Wieso Unendlich plus eins nicht größer als Unendlich ist
- Teil 3 - Gibt es größeres als unendlich?
- Teil 4 - Interessante Gedankenexperimente für die verregneten Nachmittage
Dies sind die bereits geplanten Teile der Artikelreihe. Es kann sein, dass diese Liste noch überarbeitet wird.
Wieso Unendlich plus eins nicht größer als Unendlich ist
Im letzten Teil dieser Reihe haben wir uns eine wohl vertraute, unendliche Menge angeschaut: Die Menge der natürlichen Zahlen 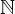 . Lasst uns also etwas genauer schauen, was Unendlichkeit bedeutet und was passiert, wenn wir ein Element hinzufügen.
. Lasst uns also etwas genauer schauen, was Unendlichkeit bedeutet und was passiert, wenn wir ein Element hinzufügen.
Eine unendliche Menge erweitern
Jetzt, da wir eine unendliche Menge zum spielen haben, probieren wir doch mal aus, was passiert wenn wir etwas hinzufügen. Was also, wenn wir auch die Zahl 0 als element in der Menge haben wollen (in Teil 1 haben wir die natürlichen Zahlen so definiert, dass 0 nicht enthalten ist). Um Verwirrung zu vermeiden geben wir dem Ganzen einen neuen Namen: 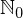 . Die mathematische Schreibweise, ein Element hinzuzufügen sieht so aus.
. Die mathematische Schreibweise, ein Element hinzuzufügen sieht so aus.
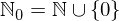
Wir nehmen die natürlichen Zahlen und vereinen sie mit der Menge, die nur die Zahl 0 enthält und wir haben die Menge, die wir wollten. Nehmen Sie sich an dieser Stelle ruhig ein wenig Zeit und versuchen eine Vorhersage zu machen, welche der Mengen die größere ist. 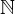 oder
oder 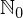 ?
?

Quelle
Unsere Intuition mag uns vorgaukeln, dass 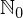 sicherlich größer sein muss als
sicherlich größer sein muss als 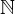 . Wir haben schließlich ein Element hinzugefügt. Doch wenn Sie auf Ihre Intuition gehört haben, dann sind Sie leider in die Irre geführt worden. Die Mengen
. Wir haben schließlich ein Element hinzugefügt. Doch wenn Sie auf Ihre Intuition gehört haben, dann sind Sie leider in die Irre geführt worden. Die Mengen 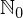 und
und 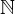 haben dieselbe Größe.
haben dieselbe Größe.
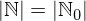
Wenn Sie mir nicht glauben oder nicht verstehen, wie das der Fall sein kann, dann lesen Sie weiter. Ich werde Sie durch jeden einzelnen Schritt führen und alles im Detail und für den Laien verständlich erklären.
Die Puzzleteile des Beweises
Achtung mathematische Formeln voraus. Seien Sie gewappnet, aber keine Angst. Alles wird ganz in Ruhe erklärt.
Das tolle an Mathematik ist, dass Sie mir nicht glauben müssen (oder sollten). Sie müssen (oder sollten) nicht einmal einem hochdekorierten Mathematikprofessor glauben. Das einzige was von Wert ist, sind Beweise. Lassen Sie mich also beweisen, was ich hier so forsch in den Raum geschmissen habe.
Einschub
An dieser Stelle sollte ich ein recht bekanntes Paradoxon bzw. Gedankenexperiment erwähnen: "Hilberts Hotel". Mir persönlich hat dieses Gedankenexperiment jedoch nicht geholfen, sondern eher nur Verwirrung gestiftet. Dies liegt daran, dass in Hilberts Hotel ein Hotel mit unendlich vielen Räumen vorgestellt wird. Etwas, was offensichtlich nicht existieren kann. Ich persönlich komme mit diesen pseudo-realen Beispielen nie gut zurecht, weshalb ich in diesem Artikel nicht weiter darauf eingehen werde. Wenn Ihnen solche Beispiele jedoch helfen, oder Sie einfach neugierig sind, dann finden Sie hier einen guten Artikel über Hilberts Hotel (S. 11 ff.).
Überlegen wir mal, wie man die Gleichheit der Größe von Mengen beweisen könnte. Wir haben zwei Mengen. Jede der Mengen hat Elemente. Wir benötigen etwas, um diese Mengen zu vergleichen. Es gibt etwas essentielles in der Mathematik, was Sie eventuell nicht mit Mengen in Verbindung bringen, wenn Sie kein Freund der Mathematik sind: Funktionen. Aus mathematischer Sicht sind Funktionen lediglich Zuordnungen von Elementen aus einer Menge zu Elementen aus einer anderen Menge. Schauen wir uns mal eine einfache Funktion an:
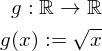
Die Funktion g ist so definiert, dass sie Elemente aus den reellen Zahlen anderen Elementen aus den reellen Zahlen zuordnet. Insbesondere ordnet sie einer Zahl x die Quadratwurzel derselben Zahl zu. Die meisten Funktionen, denen man begegnet sind auf den reellen Zahlen definiert, aber auch die Menge der reellen Zahlen ist nur eine Menge. Wir können uns frei entscheiden, auf was für Mengen wir eine Funktion definieren wollen.
Eine Funktion sie zu knechten
Bauen wir uns also eine Funktion, um die zwei Mengen 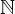 und
und 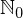 zu vergleichen indem wir unsere Funktion von
zu vergleichen indem wir unsere Funktion von 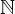 nach
nach 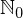 abbilden lassen.
abbilden lassen.
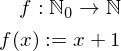
Mit unseren recht begrenzten Mengen müssen wir kurz prüfen, ob diese Funktion überhaupt gültig ist. Die Funktion darf keine Elemente zurückgeben, die nicht in 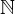 sind, egal welches Element aus
sind, egal welches Element aus 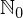 wir ihr geben. Prüfen wir also den Grenzfall, sprich das kleinste Eingabeelement
wir ihr geben. Prüfen wir also den Grenzfall, sprich das kleinste Eingabeelement 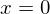 .
.
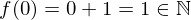
(Wir erinnern uns
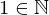 bedeutet, dass 1 ein Element von
bedeutet, dass 1 ein Element von 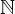 ist.)
ist.)Das sieht gut aus. Wie sieht es denn mit anderen Elementen aus. Naja, für alle 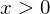 haben wir kein Problem mit Grenzen, da wir nur etwas addieren und somit nie Zahlen unter 1 erhalten. Die Funktion liefert auch keine rationalen oder irrationalen Zahlen, sondern immer nur ganze, da wir nur eine ganze Zahl addieren. (Das war ein sehr informeller Beweis zum Zwecke der Leserlichkeit.)
haben wir kein Problem mit Grenzen, da wir nur etwas addieren und somit nie Zahlen unter 1 erhalten. Die Funktion liefert auch keine rationalen oder irrationalen Zahlen, sondern immer nur ganze, da wir nur eine ganze Zahl addieren. (Das war ein sehr informeller Beweis zum Zwecke der Leserlichkeit.)
Wir haben also eine Funktion gefunden, die von der einen in die andere der zwei Mengen, die wir vergleichen wollen, abbildet. Doch wollten wir nicht beweisen, dass sie dieselbe Größe haben? Wie kann uns denn eine Funktion da helfen? Wie in kürze offenbar werden wird, war die Wahl dieser Funktion nicht zufällig. Die gewählte Funktion hat ein paar nützliche Eigenschaften, die uns bei dem Beweis helfen werden.
Bijektive Funktionen
Unsere Funktion 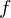 ist bijektiv. Bijektiv bedeutet, sie ist sowohl injektiv als auch surjektiv (klar...).1 Das hilft natürlich nicht als Erklärung, also im Detail was injektiv und surjektiv bedeutet:
ist bijektiv. Bijektiv bedeutet, sie ist sowohl injektiv als auch surjektiv (klar...).1 Das hilft natürlich nicht als Erklärung, also im Detail was injektiv und surjektiv bedeutet:
Unsere Funktion ist injektiv, wenn keine zwei unterschiedlichen Elemente aus 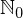 auf dasselbe Element aus
auf dasselbe Element aus 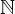 abgebildet werden. Anders formuliert, wenn man das Ergebnis der Funktion ansieht, dann weiß man ganz genau welches Eingabeelement dieses Ergebnis produziert hat, weil es nur genau ein solches Element gibt.2
abgebildet werden. Anders formuliert, wenn man das Ergebnis der Funktion ansieht, dann weiß man ganz genau welches Eingabeelement dieses Ergebnis produziert hat, weil es nur genau ein solches Element gibt.2
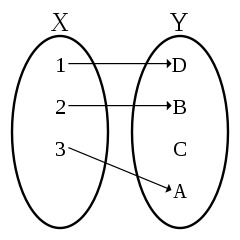
Quelle
Surjektiv bedeutet wiederum, dass alle Elemente der Ausgabemenge erreicht werden können indem man ein Element der Eingabemenge in die Funktion gibt. Anders formuliert, es existiert kein Element in der Ausgabemenge, welches nicht durch die Funktion und die Eingabemenge erzeugt werden kann.3
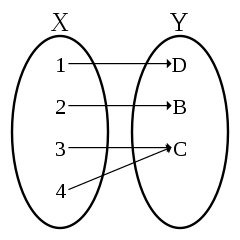
Quelle
Auch hier, wieder kein formeller Beweis um den Artikel leserlich zu machen: Da die Funktion 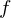 die Zahl 1 zu der Eingabe addiert, werden keine zwei Eingaben auf dieselbe Ausgabe abgebildet, sprich die Funktion ist injektiv. Da die Eingabemenge
die Zahl 1 zu der Eingabe addiert, werden keine zwei Eingaben auf dieselbe Ausgabe abgebildet, sprich die Funktion ist injektiv. Da die Eingabemenge 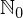 unendlich groß ist und somit niemals zuende geht, können wir auch alle Elemente der Ausgabemenge
unendlich groß ist und somit niemals zuende geht, können wir auch alle Elemente der Ausgabemenge 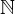 erzeugen. Die Funktion
erzeugen. Die Funktion 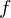 ist surjektiv.
ist surjektiv.
Wer interesse an einem formellen Beweis für die Bijektivität dieser Funktion hat, kann den formellen Beweis hier finden.
Zusammensetzen der Puzzleteile
Folgendes haben wir erarbeitet.
- Unsere Menge
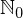 ist die Menge aller natürlichen Zahlen und der Zahl 0.
ist die Menge aller natürlichen Zahlen und der Zahl 0. - Wir haben eine Funktion
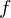 gefunden, die von
gefunden, die von 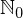 nach
nach 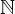 abbilden kann.
abbilden kann. - Diese Funktion ist bijektiv.
Fassen wir nochmal zusammen, was bijektiv bedeutet. Unsere Funktion ist genau dann bijektiv, wenn jedes verschiedene Element aus 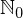 auf ein eindeutiges Element aus
auf ein eindeutiges Element aus 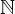 abgebildet wird und wenn alle Elemente aus
abgebildet wird und wenn alle Elemente aus 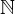 auch wirklich abgebildet bzw. "erreicht" werden.
auch wirklich abgebildet bzw. "erreicht" werden.
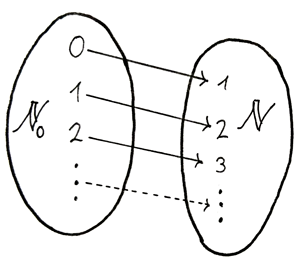
Bild von mir
Es existiert also eine bijektive Abbildung (anderes Wort für Funktion) von 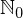 nach
nach 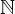 . Das bedeutet wir bilden nie zwei mal auf das selbe Element aus
. Das bedeutet wir bilden nie zwei mal auf das selbe Element aus 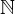 ab und uns gehen die Elemente von
ab und uns gehen die Elemente von 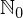 nie aus, wir erreichen alle Elemente aus
nie aus, wir erreichen alle Elemente aus 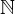 . Also müssen beide Mengen dieselbe Größe haben!
. Also müssen beide Mengen dieselbe Größe haben!
Wäre die Eingabemenge größer, dann wären wir gezwungen mehrere Eingaben auf dieselbe Ausgabe abzubilden (uns würden die Ausgaben ausgehen). Das hätte zur Folge, dass keine injektive Funktion existieren kann.
Wäre die Ausgabemenge größer, dann könnten wir nicht alle Elemente der Ausgabemenge erreichen (uns würden die Eingaben ausgehen). Das hätte zur Folge, dass keine surjektive Funktion existieren kann.
Wir haben jedoch eine bijektive Funktion von 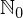 nach
nach 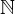 gefunden, also müssen beide Mengen dieselbe Größe haben. Obwohl wir zu einer der Mengen ein Element hinzugefügt haben.
gefunden, also müssen beide Mengen dieselbe Größe haben. Obwohl wir zu einer der Mengen ein Element hinzugefügt haben.
Im allgemeinen lässt sich sagen, dass zwei Menge genau dann die selbe Größe haben, wenn eine bijektive Abbildung von der einen in die andere Menge finden lässt.4 Gießen wir das in einen mathematischen Ausdruck, so sieht das so aus.
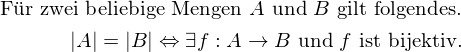
(
 bedeutet "es existiert ein...")
bedeutet "es existiert ein...")Einschub
Es ist sicherlich nicht jedem aufgefallen, doch ich habe in der Formulierung oben "genau dann" verwendet. Das Wort "genau" hat hier eine ganz bestimmte mathematische Bedeutung: Zu sagen "A gilt genau dann, wenn B gilt" bedeutet wenn A wahr ist muss auch B wahr sein, aber genauso gilt wenn A falsch ist muss auch B falsch sein. Ohne das Wörtchen "genau" wäre die Aussage eine Implikation und keine Äquivalenz. "A gilt wenn B gilt" bedeutet nur, dass A wahr ist wenn B wahr ist, jedoch können wir keine Aussage über A treffen, wenn wir wissen dass B falsch ist.

Quelle
Ergebnis
Wir haben soeben bewiesen, dass das Hinzufügen eines Elements zu einer unendlichen Menge, die Größe dieser Menge nicht verändert.
Tatsächlich können wir eine beliebige endliche Anzahl an Elementen hinzufügen. Wir müssen unsere Funktion nur so anpassen, dass wir eine entsprechend größere Zahl zu der Eingabe hinzuaddieren.
Beeindruckend, finden Sie nicht?
Doch bedeutet das, dass es nur eine Art Unendlichkeit gibt und dass alle Unendlichkeiten dieselbe Größe haben? Nein, keineswegs! Wenn Sie neugierig sind Menge zu sehen, die größer als die Menge der natürlichen Zahlen sind, dann bleiben sie gespannt für den nächsten Teil dieser Serie.
In der Zwischenzeit hoffe ich, es war interessant und verständlich. Sollten Sie irgendwelche Fragen haben, mehr formelle Beweise sehen oder einfach ein kurzes Feedback da lassen wollen, dann sind die Kommentare unten genau richtig für Sie.
Mehr Spaß?
Es gibt natürlich mehr Mengen, die auf den ersten Blick erscheinen als müsste eine größer sein als die Andere. Hier ein paar Beispiele. Wenn Sie wollen, dann versuchen Sie doch einmal selbst eine bijektive Abbildung zu finden, um zu beweisen dass sie dieselbe Größe haben. Ich helfe auch gerne in den Kommentaren dabei.
Nach Schwierigkeit sortiert (einfachstes zuerst):
- Die Menge aller geraden Zahlen
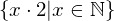 (gelesen als "die Menge aller x mal 2 mit allen x aus den natürlichen Zahlen") und die Menge der natürlichen Zahlen.
(gelesen als "die Menge aller x mal 2 mit allen x aus den natürlichen Zahlen") und die Menge der natürlichen Zahlen. - Die Menge aller ganzen Zahlen
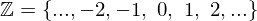 und die Menge der natürlichen Zahlen. Tipp: Die Funktion muss zwar eine bijektive Abbildung sein, aber sie muss nicht monoton sein. Sprich, die Werte dürfen springen soviel Sie wollen.
und die Menge der natürlichen Zahlen. Tipp: Die Funktion muss zwar eine bijektive Abbildung sein, aber sie muss nicht monoton sein. Sprich, die Werte dürfen springen soviel Sie wollen. - Die Menge aller natürlichen Zahlen und die Menge aller rationalen Zahlen
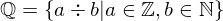 . Dies ist jedoch etwas schwieriger und wird unter anderem Thema des nächsten Teils sein.
. Dies ist jedoch etwas schwieriger und wird unter anderem Thema des nächsten Teils sein.
- Bijektive Funktionen - https://de.wikipedia.org/wiki/Bijektive_Funktion
- Injektive Funktionen - https://de.wikipedia.org/wiki/Injektive_Funktion
- Surjektive Funktionen - https://de.wikipedia.org/wiki/Surjektive_Funktion
- Die einzige Quelle, die ich finden konnte, ist ein nicht öffentlich zugängliches Skript meines Professors für Komplexitätstheorie. Sollten Sie eine öffentliche Quelle hierzu kennen, posten Sie die bitte in den Kommentaren.
- Hilberts Hotel - S. 11 ff. http://www.mathematik.uni-marburg.de/~bschwarz/Sem_09W_files/10%20Daniel%20Rausch%20-%20Hilberts%20Hotel.pdf
Hinweis: Die meisten Beweise waren informelle Beweise, um den Artikel leserlich zu gestalten. Wenn Sie formelle Beweise sehen möchten, dann lassen Sie es mich in den Kommentaren wissen.
Gleichungen erzeugt mit latex2png.
This is a test comment, notify @kryzsec on discord if there are any errors please.
Being A SteemStem Member
This is a test comment, notify @kryzsec on discord if there are any errors please.
Being A SteemStem Member
.
Freut mich, dass dir der Artikel gefallen hat und du dir sogar Gedanken über die Quizfragen gemacht hast.
.
Teil 3 ist fertig.
English version here.
Dies. Genau so erging es mir jedes mal, wenn ich mir Videos zur Unendlichkeit angeschaut habe, und Hilberts Hotel erwähnt wurde.
Durch deine Erklärung dagegen hab ich endlich verstanden, was damit eigentlich gezeigt werden will.
Guter Artikel!
Freut mich sehr, dass ich deine Verwirrung auflösen konnte!
Ich habe die Verbindung zwischen Hilberts Hotel und bijektiven Abbildungen auch erst erkannt, lange nachdem ich von beiden Dingen getrennt erfahren habe.
erneut sehr nice, weiter so!
Einer der besten Artikel mit dem de-stem Tag! Definitiv ein Upvote wert.
Evtl. könnte man noch auf eine Liste Mathematischer Symbole verweisen oder den "aus B folgt A - Pfeil" für Neulinge kurz erklären.
Vielen Dank. Ich schaue mal ob ich es morgen schaffe eine kleine Liste der verwendeten mathematischen Symbole zu erstellen.