Simple Interest and Compound Interest

Summary

• Interest is the cost of borrowing a certain amount of money from an individual or a financial institution.
• Simple Interest is where the interest paid is calculated on the original amount of the loan.
• Compound Interest is where the interest paid is calculated on the current net sum of the loan after the last time interest was collected.
• This amount that the bank loans on someone's credit card is usually compounded daily, and is at a high interest rate due to it's accessibility and ease of access to such high amounts of funds. That is why it is always advantageous to pay off a loan that has compound interest as quickly as possible.

Introduction
"The most powerful force in the world is compound interest" - Albert Einstein

Interest is the cost of borrowing a certain amount of money from an individual or a financial institution. In this blog, we will discuss the two types of interests and how they differ from one another; simple interest and compound interest. It should be noted, 'the principal', refers to the original

Simple Interest
Simple Interest is where the interest paid is calculated on the original amount of the loan. The principal here refers to the original amount of the loan. The calculation for simple interest is shown in Figure 1.

Figure 1

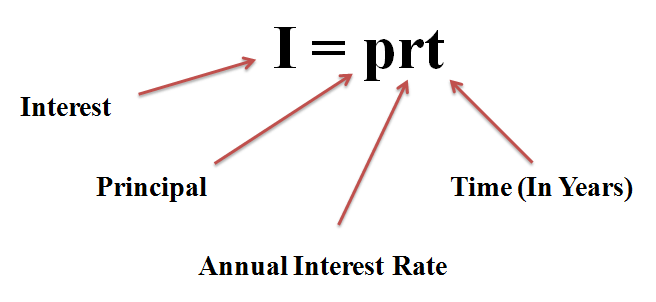
Source: Statistic Lectures n.d.

Example 1: Normal equation use
If you invested a loan of $10,000 as a principal, with an annual interest rate of 3%, after 4 years, how much interest would you make?

• If I = p * r * t
• Then I = $10,000 * 0.03 * 4 = $1,200

Therefore, you would have made $1,200 dollars in interest at 3% over 4 years. You can add this value together with the principal to get the total value of your investment.

• $1,200 + $10,000 = $11,200

Example 2: When using days
If you invested a loan of $10,000 as a principal, with an annual interest rate of 3%, after 300 days, how much interest would you make?

• If I = p * r * t
• Then I = $10,000 * 0.03 * 300/365 = $246.575 (to 3 decimal places)

Example 3: Finding other factors
If you need to find other factors, such as p, r or t, then you can rearrange the equations to find them.

• If I = p * r * t
• Then: I = p * r * t, p = I/(r * t), r = I/(p * t), t = I/(p * r)

Uses in Reality
Calculating simple interest can be used for a variety of factors to calculate interest. Some of these are listed below.

• Certificate of Deposits: These are certificates handed out by the bank, where if you deposit a certain amount of money with them, they will pay you that amount plus a certain percentage of interest over a given time.
• Consumer loans for home appliances such as refrigerators, washing machines and freezers.
• Payday loans: These are loans that that you can get from certain financial institutions that will get you quick cash for a high interest percentage.

Compound Interest
Compound Interest is where the interest paid is calculated on the current net sum of the loan after the last time interest was collected. The principal here refers to the the current net sum of the loan after the last time interest was collected. The calculation for compound interest is shown in Figure 2.

Figure 2

Source: The Calculator Site, n.d.

Example 1: Normal equation use
If you deposit $10,000 as a principal into a bank account, with a interest rate of 3% per annum compounded annually, after 4 years, how much would you make?

• If A = P(1+(r/n))^(nt)
• Then A = $10,000(1+(0.03/1))^(1 * 4) = $11,255.09

To find out how much money you have made, subtract P from A

• Amount made/lost = A - P = $11,255.0881 - $10,000 = $1,255.09

Example 2: different payable periods
If you deposit $10,000 as a principal into a bank account, with a interest rate of 3% per annum compounded quarterly, after 4 years, how much would you make?

• If A = P(1+(r/n))^(nt)
• Then A = $10,000(1+(0.03/4))^(4 * 4) = $11,269.92

Example 3: The power of compound interest
If you deposit $10,000 as a principal into a bank account, with a interest rate of 3% per annum compounded daily, after 4 years, how much would you make?

• If A = P(1+(r/n))^(nt)
• Then A = $10,000(1+(0.03/365))^(365 * 4) = $11,274.91

Notice the values of each of these three examples calculated. The more times the interest rate is compounded per year, the greater the ending amount you make.

Uses in Reality
Calculating compound interest can be used for a variety of factors to calculate interest. Compound interest is primarily used for any types of large money loans such as Mortgage, Equipment and Investment loans. This is used in equipment loans (eg. a tractor) because the business can use the equipment to create revenue for their business, which means the bank is able to gain more money if the business is using that equipment to create revenue. Compound interest is also used in mortgage loans. Firstly because it creates a psychological incentive to pay back a large amount of money as soon as possible. Secondly, it can ease the burden of mortgage borrowers when they start paying back their loans, improving their experience with their financial lender.

The power of compound interest
Whenever obtaining a loan, understand the interest that is paid on a loan. A lot of people use credit cared debt in order to purchase certain items when they do not have the cash. This amount that the bank loans on someone's credit card is usually compounded daily, and is at a high interest rate due to it's accessibility and ease of access to such high amounts of funds. This usually will rack up a huge amount of debt if it is gone unnoticed or unpaid.

For example, say you used your credit card to buy new shoes that are $150. The bank will loan you that $150, at an interest rate of 12% per annum compounded daily.

• If A = P(1+(r/n))^(nt)
• Then A = $150(1+(0.12/365))^(365 * 1) = $169.12
  This means, if you leave the loan unchecked and unpaid for a year, you will have to pay $19.12 more for your shoes. That is a %12.74 (from calculating the percentage increase between A and P = 100 * ((169.12-150)/150)) increase on the amount you paid for your shoes.

Doing this with higher amounts of money, such as a property of $500,000 or more could land you in some serious trouble down the road. That is why it is always advantageous to pay off a loan that has compound interest as quickly as possible. To not only reduce the amount of debt to pay off, but also to reduce the repayments you will need to make per time period set.

For example with the shoes, if after a year you paid off $100 of your debt borrowed, that is currently now $169.12, your interest rate would not only be lower, but the amount you have to pay back would also be lower.

• If A = P(1+(r/n))^(nt)
• Then A = ($169.12-$100)(1+(0.12/365))^(365 * 1) = $77.93

Therefore, the amount you would have to pay back now is $77.93, and the interest payment on that per annum would be $9.93 (See below). As opposed to $19.12 if you did not pay back $100 after a year.

• If A = P(1+(r/n))^(nt)
• Then A = ($77.93)(1+(0.12/365))^(365 * 1) = $87.864
• $87.86 - $77.93 = $9.93

Never forget how powerful compound interest is. Whenever you take out a loan to invest, buy a house or for expenses, compound interest will in most cases, be there to make you repay your debts.

Source

• Statistics Lectures n.d., 'Simple Interest', Statistics Lectures, retrieved 27 June 2017, http://www.statisticslectures.com/topics/simpleinterest/
• The Calculator Site n.d., 'Compound Interest Formula - Explained', The Calculator Site, retrieved 27 June 2017, http://www.thecalculatorsite.com/articles/finance/compound-interest-formula.php