시간 간 자연스러운 결정 전략 모델링 (5) - 개별 거래 게임 모델 (시장에 관한 변수)
이번 글에서는 앞선 글을 기준으로 개별 거래 게임 모델 중 시장에 관한 변수를 살펴보도록 하겠습니다.
전략형 게임 변수
(시간 법칙 1) 적절한 시간에 이루어진 결정은 게임 참여자들 내적 이익 분배 우위 왜곡을 덜어줌
(시간 법칙 2) 적절한 시간에 이루어진 결정은 게임 참가자들 사이에서 세부 사항에 대한 불만 없는 합의로 이어짐
전개형 게임 변수
(공간 법칙 1) 각 게임 플레이어는 스스로가 가장 유리한 위치에서 게임을 진행하고자 노력함
(공간 법칙 2) 약자는 강자의 가장 약한 지점을 노리며, 강자는 스스로의 강점이 가장 잘 드러나는 지점을 게임 장소로 선호함
전략-전개 게임 변수의 상호 작용
시간 법칙 1 + 공간 법칙 1 - 시장 참가자는 상대 시장 참가자의 내적 이익 분배를 저하 하기 위해 상대가 선호하는 시장 선택을 방해할 수 있다.
시간 법칙 1 + 공간 법칙 2 - 시장 참가자는 상대 시장 참가자가 선호하는 시장 선택을 방해하기 위해 상대 시장 참가자의 내적 이익 분배를 저하할 수 있다.
시간 법칙 2 + 공간 법칙 1 - 시장 참가자는 시장 세부 사항 확정을 근거로 상대 시장 참가자가 선호하는 시장이 아닌 시장을 선택하려 한다.
시간 법칙 2 + 공간 법칙 2 - 시장 참가자는 상대 시장 참가자가 선호하는 시장이 아닌 시장을 통해 시장 세부 사항 확정을 확정하려 할 수 있다.
시장 참여자(MP)는 집합으로서 이익을 분배 받는 구성원(M)들로 구성되어 있습니다.

시간 법칙 1과 2에 대해 살펴보겠습니다. 시간 법칙 1과 2는 내적 이익 분배 함수(IDD)에 대해 개인의 불만(ID)을 제외한 각 개인의 효용의 합이 최대화될 때가 거래의 적절한 시간임을 의미합니다.

위와 같이 최적화 거래 시간 t가 도출됩니다.
공간 법칙 1과 2에 대해 살펴보겠습니다. 공간 법칙 1과 2는 공간의 변동에 따라 갖게 되는 전체 효용이 달라질 수 있으므로 시장에 참여하고자 할 때 본인에게 가장 유리한 시장을 선택한다는 것을 의미합니다. 이를 수식적으로 표현하기 위해 다시 해석하자면, 거래가 이루어지는 시장은 주어진 시장들 중 특정 시점에 시장 참여자의 거래를 통한 효용의 합이 가장 극대화 되는 곳이라는 의미를 가집니다.
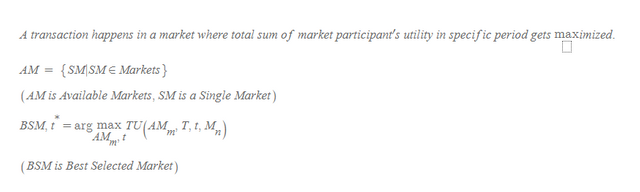
이 다음 전략-전개 게임 변수의 상호 작용을 살펴볼 수 있습니다. 시간 법칙 1 + 공간 법칙 1, 시간 법칙 2 + 공간 법칙 1에 의하면 상대방이 선호하는 시장에 대한 방해가 발생합니다. 시간 법칙 1 + 공간 법칙 2, 시간 법칙 2 + 공간 법칙 2에 의하면 상대방이 선호하지 않는 시장에 의해 발생하는 내적 이익 분배를 저하와 시장 구성원의 불만을 이야기하고 있습니다. 이를 수식으로 나타내자면 다음과 같습니다.

자, 여기까지 시장에 관한 변수를 살펴보았습니다. 다음으로 시장 참여자의 인식, 기회, 기억의 오류를 살펴보도록 하겠습니다.