Sly mathematics. Geometric illusion or the devil - in detail/Хитрая математика. Геометрическая иллюзия или дьявол - в деталях

Sometimes schoolboys throw me some mathematical puzzles. This happens rarely, that's why every such situation is perceived by me as a small holiday (mummies are interesting for mathematics!) And remembered. Especially when I can not decide what they brought.
The story with the geometric puzzle happened a long time ago, but I remember it very well. Moreover, when I got to the truth, I laughed at myself.
So, on one of the changes before the lesson, the kindery slipped me a notebook with a geometric figure.
Иногда школьники подкидывают мне какие-нибудь математические головоломки. Случается это редко, поэтому каждая такая ситуация воспринимается мною как небольшой праздник (балбесам интересна математика!) и запоминается. Особенно, когда я не могу решить то, что они притащили.
История с геометрической головоломкой случилась уже давно, но я её помню очень хорошо. Тем более, что, когда я докопался до истины, то хохотал над собой.
Итак, на одной из перемен перед уроком киндеры подсунули мне тетрадный листок с геометрическим рисунком.
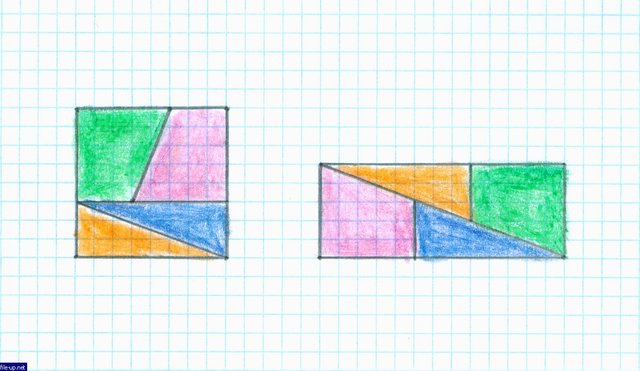
They say: "Look - the square was cut into pieces and the rectangle was folded out of them."
"Well, cool," - I answer them, not stopping from filling the journal.
"Of course," small barmalies agree. "And find the square of the square."
And what to look for it? Eight cell side. So multiply eight by eight, we get 64.
"Sixty-four," I tell them, figuring out how to fix the incorrectly written topic of the lesson.
"And now the area of the rectangle," - they are not appeased.
Here is the people. Quite stupid, they check me for knowledge of the simplest formulas. I count the cells, length - thirteen, width - five. We multiply ...
"Sixty-five. And do not bother me with your magazine to work."
"And how?" The children almost shouted, "It must be the same!"
I again look at the drawing ... And put off the boring magazine aside. In fact, some garbage is obtained. The square has an area of 64, and a rectangle composed of the same pieces - 65.
Говорят: "Смотрите - квадрат разрезали на части и сложили из них прямоугольник".
"Ну, клёво", - отвечаю я им, не отрываясь от заполнения журнала.
"Конечно, - соглашаются маленькие бармалеи. - А найдите-ка площадь квадрата".
А что её искать? Восемь клеток сторона. Значит, умножаем восемь на восемь, получаем 64.
"Шестьдесят четыре", - отвечаю я им, прикидывая, как исправить неверно записанную тему урока.
"А теперь площадь прямоугольника", - не унимаются они.
Вот народ. Совсем поглупели, проверяют меня на знания простейших формул. Считаю клеточки, длина - тринадцать, ширина - пять. Перемножаем...
"Шестьдесят пять. И не мешайте мне с вашим журналом работать".
"А как так?! - почти кричат детки. - Ведь должно быть одинаково!"
Я опять гляжу на рисунок... И откладываю скучный журнал в сторону. В самом деле, какая-то фигня получается. У квадрата площадь - 64, а у прямоугольника, составленного из тех же кусочков - 65.
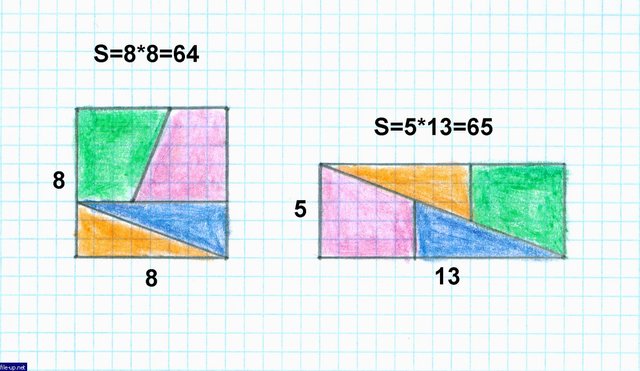
Here begins a saving lesson, during which I periodically stupidly look at the picture with a puzzle, trying to figure out what the chip is. Figures from which a square and a rectangle consist - a pair of equal trapezoids, and a pair of equal rectangular triangles. I estimate the sum of their areas:
Тут начинается спасительный урок, в течение которого я периодически тупо смотрю на картинку с головоломкой, пытаясь понять в чём фишка. Фигуры, из которых состоят квадрат и прямоугольник - пара равных трапеций, и пара равных прямоугольных треугольников. Прикидываю сумму их площадей:
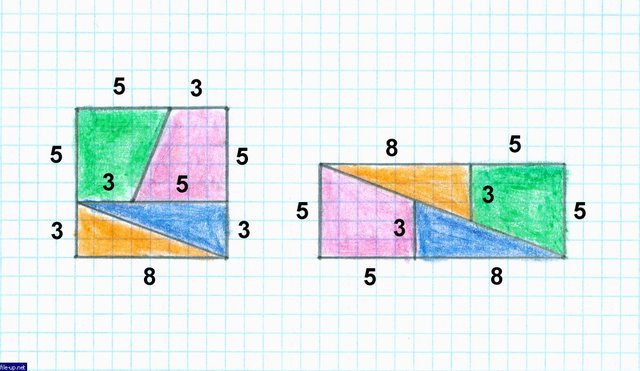
Trapezoid: 5 * (5 + 3) = 40, triangles: 3 * 8 = 24, the sum: 40 + 24 = 64. That's right, everything converges ... but only for a square. The bell rings.
"I have not figured it out," I confess to the students. "I'll think until tomorrow."
Probably, it makes no sense to say that all the remaining time at work, as soon as free minutes fell out, I went back to this accursed drawing.
The answer was clearly hidden in the rectangle; not he was the original figure, which means that his area was different from the reference one. I carefully examined the picture. Why its area was more than 1 unit? After all, made up of the same figures! How did 64 become 65? Or not out of equals?
And what if we draw it bigger? I take a new sheet, zoom in and out! But the triangles, from which this fucking rectangle is composed, are not exactly the same as in the square! Smaller legs they have a little more. Quite a bit, but more!
Трапеции: 5х(5+3)=40, треугольники: 3х8=24, сумма: 40+24=64. Всё верно, всё сходится... но только для квадрата. Звенит звонок.
"Я не разгадал, - признаюсь ученикам. - Буду думать до завтра".
Наверное, нет смысла говорить о том, что всё оставшееся время на работе, как только выпадали свободные минуты, я возвращался к этому проклятому рисунку.
Ответ явно скрывался в прямоугольнике, т.к. не он был исходной фигурой, а значит именно его площадь отличалась от эталонной. Я внимательно рассматривал картинку. Почему его площадь оказывалась больше на 1 единицу? Ведь составлен из тех же самых фигур! Как 64 стало 65? Или не из равных?
А что, если начертить его покрупнее? Беру новый листок, увеличиваю масштаб и - опаньки! А ведь треугольники, из которых составлен этот чёртов прямоугольник, не точно такие же как в квадрате! Меньшие катеты у них немножко больше. Совсем на чуть-чуть, но больше!
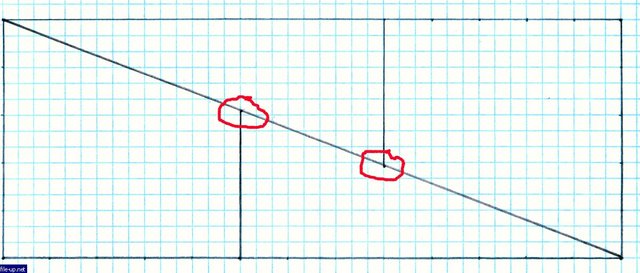
And if in their place put triangles from the square, their hypotenuse will not form the diagonal of the rectangle, and a small alkali appears, which gives an extra unit to the area.
И если на их места положить треугольники из квадрата, то их гипотенузы не будут образовывать диагональ прямоугольника, а появляется небольшая щёлочка, которая и даёт лишнюю единицу к площади.
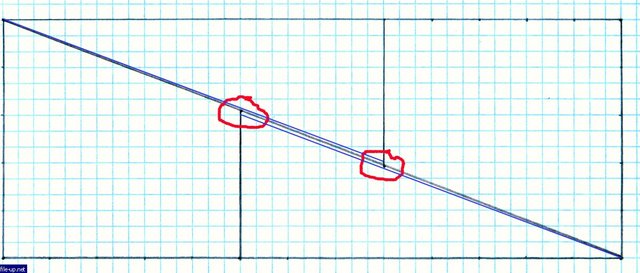
But it will be visible only at a large scale!
Но видно это будет только при большом масштабе!

And if you return the picture to the previous cells of the student's notebook, the puzzle again becomes insoluble.
My joy was boundless. And, from the previously solved much more difficult tasks, I did not get such pleasure as from this, found unknown where one of my students. And for myself, I concluded that we should take more care of the little things.
And remember that knowledge is power!
И если вернуть рисунок на прежние клеточки ученической тетради, то головоломка опять становится неразрешимой.
Моей радости не было предела. Причём, от решённых ранее гораздо более сложных задач я не получал такого удовольствия как от этой, найденной неизвестно где одним из моих учеников. А для себя я сделал вывод - надо тщательнее относиться к мелочам.
И помнить, что знания - сила!
You got a 33.33% upvote from @sunrawhale courtesy of @filinpaul!
This service has been created with the help of @yabapmatt so please show your support by voting for him for witness!
This post has received a 2.88% upvote from @aksdwi thanks to: @filinpaul.
Your Post Has Been Featured on @Resteemable!
Feature any Steemit post using resteemit.com!
How It Works:
1. Take Any Steemit URL
2. Erase
https://3. Type
reGet Featured Instantly & Featured Posts are voted every 2.4hrs
Join the Curation Team Here | Vote Resteemable for Witness
Thank you so much for using our service! You were protected from up to 20% losses!
Help us grow by delegating to us! 100sp, 500SP, 1000SP, ANY SPYou just received 23.11% upvote from @onlyprofitbot courtesy of @filinpaul!
Hey @filinpaul, Congratulations !!! We just upvoted your post with 25.00% power. Keep up the good work. Join our discord channel https://discord.me/SteemBulls