▲ ▲ ▲ Finite fields in beautiful pictures [48 lines of code]
Hello, Steemians! Today I want to introduce to you the finite fields. So I decided to make some popularisation article.
All pictures in article are made and designed by me. The same for code (requires C++ IDE and glut installed to run - ask in comments for more).
Let's go!
Okay, first I should say what is finite field in general words?
It is a finite set with special properties and defined operations. That defined so if we made an operation on two elements of finite field we will get element of finite field (another).
First we say, that module ring over the prime module p is ... finite field.
So now we will observe the set of modules over p. So, that's enough boring theory :-)
Then we talk about ... multiplication table.
Everyone knows what is it and of course we can construct such a table for our set.
For example for p = 2 it will be like:
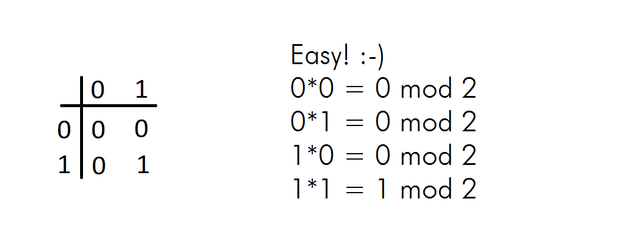
And what if we want to construct really big tables for p>10?
It'll bw rows and columns of black and white numbers. Boring.
Wait!
What if we interpolate the colors and values of table?
Besides we can use not only mutiplication function :-)
I wrote a simple programm on C++ in 48 lines of code. See the results! :-)
First we try trivial functions: f(x, y) = x mod 41 and f(x, y) = y mod 41:
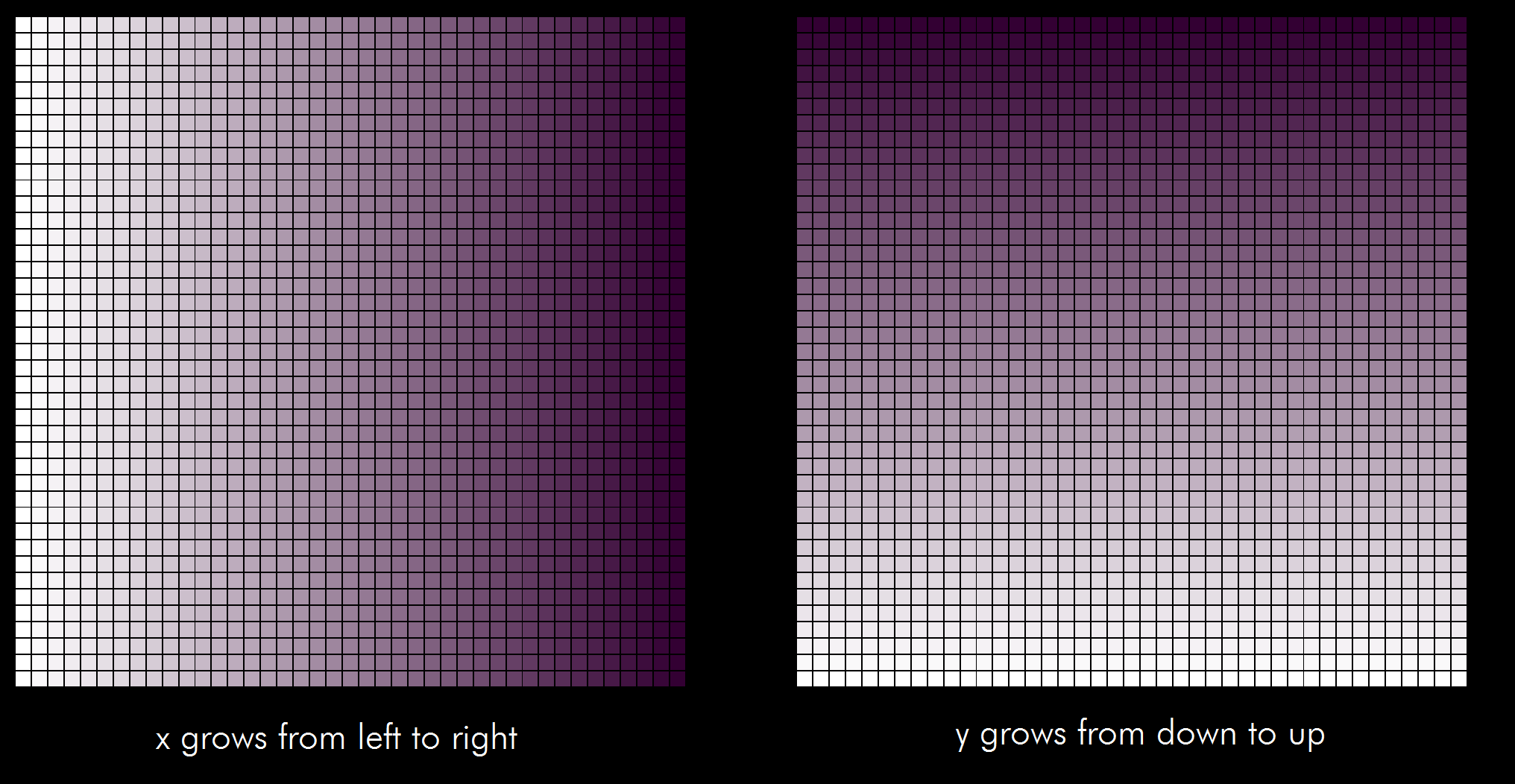
Then some more interesting - addition and multiplication:
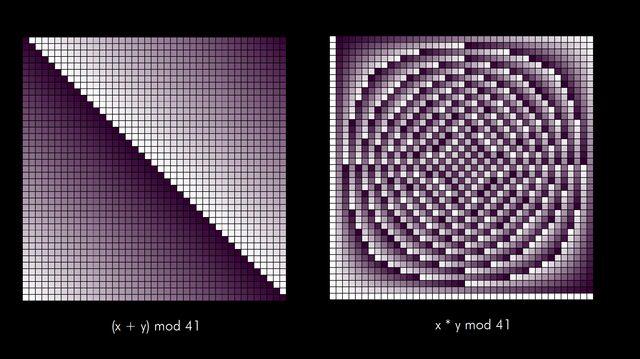
Finally, we can think up more complicated dependencies and see the results:
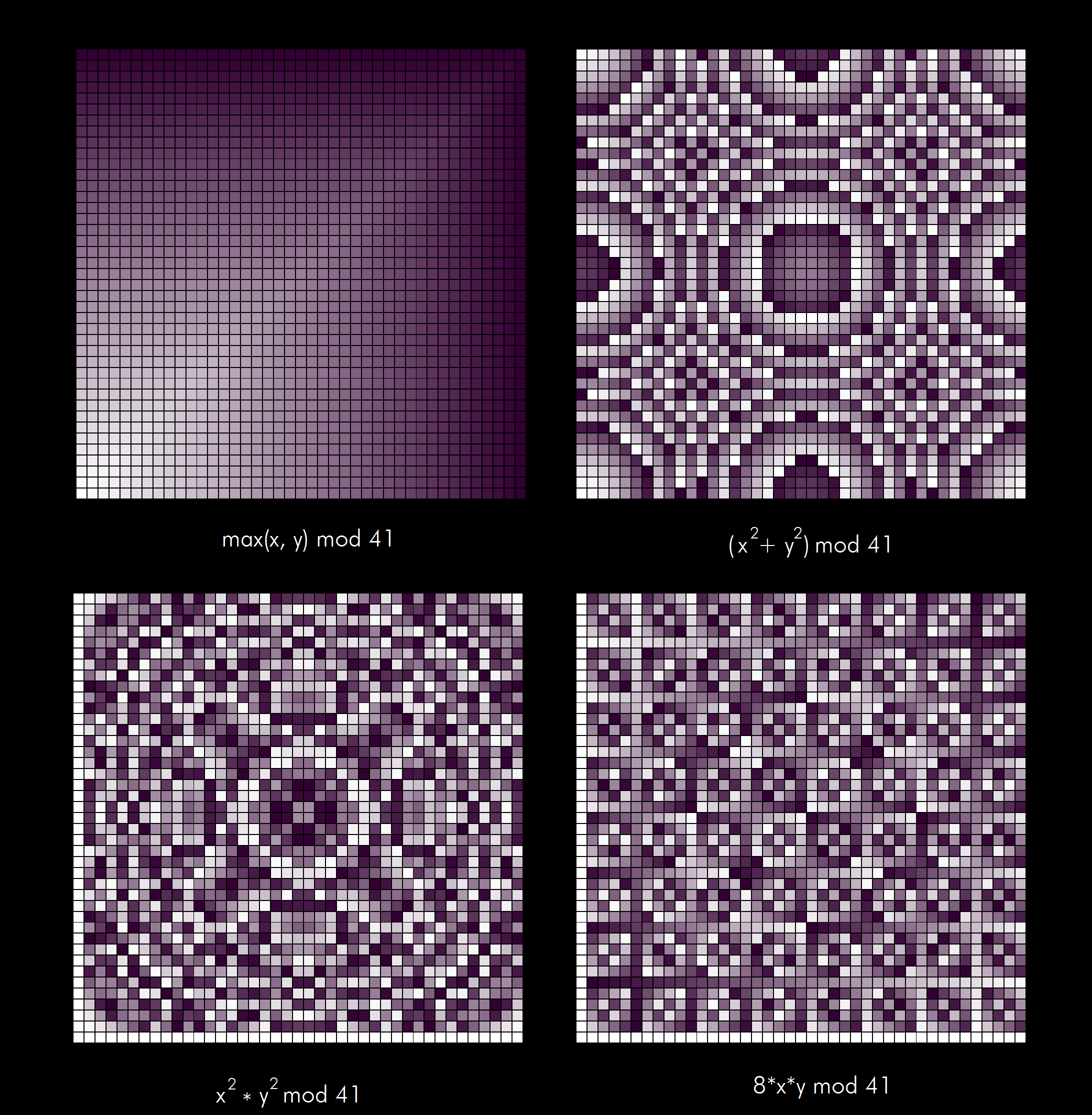
Math is beautiful indeed. I like that periodic mosaics.
My code:
#include <glut.h>
int max(int a, int b){ return (a < b) ? b : a; }
void resize(int width, int height) {
glutReshapeWindow( 1000, 1000 );
}
void DrawSquare(float xc, float yc, float s, double value)
{
glColor3f(1.0 - 0.02 * value, 1.0 - 0.025 * value, 1.0 - 0.02 * value);
glBegin(GL_QUADS);
glVertex3f( xc - s , yc + s , 0.0f ); // left up
glVertex3f( xc + s , yc + s , 0.0f ); // right up
glVertex3f( xc + s , yc - s , 0.0f ); // right down
glVertex3f( xc - s , yc - s , 0.0f ); // left down
glEnd();
}
void renderScene(void) {
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glEnable(GL_DEPTH_TEST);
int mod = 41;
for(int x = 0; x < mod; ++x)
for(int y = 0; y < mod; ++y)
DrawSquare(-0.9 + x * ( 1.8 / mod), -0.9 + y * (1.8 / mod), 0.02, ( x*y ) % mod );
glutPostRedisplay();
glutSwapBuffers();
}
void keyPressed (unsigned char key, int x, int y) {
}
int main(int argc, char **argv) {
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_DEPTH | GLUT_DOUBLE | GLUT_RGBA);
glutInitWindowPosition(50, 50);
glutInitWindowSize(1000, 1000);
glutCreateWindow("Finite fields for Steemit 9/9/17");
glClearColor( 0, 0, 0, 1);
glutDisplayFunc(renderScene);
glutReshapeFunc(resize);
glutKeyboardFunc(keyPressed);
glutMainLoop();
return 1;
}
I can continue article about Finite fields by adding some facts about Galois fields.
Does anyone interested? Let me know.
Thank you for your attention! Follow my blog @ideamaker for more :-)