reporte Análisis estático estructural: analítico y por solucionador NXnastran
Instituto Tecnológico de Chihuahua

Materia: Diseño e ingeniería asistido por computadora.
Lunes, miércoles y viernes de 1-3 P.M.
Profesor: Ing. Carlos Arturo Méndez Herrera.
Proyecto:
Análisis estático estructural: analítico y por solucionador NXnastran
Samuel Esteban Gutiérrez Martínez. 09061215
13 de Junio de 2014
Definición del problema
El siguiente es un análisis estático estructural. Con cargas combinadas.
Elemento a diseñar
Seleccionar un tubo que soportara unas cargas.
Justificación
Un ingeniero además de ser capaz de dar una solución analítica y compararla con el resultado de un programa computacional, debe interpretar los resultados de la solución y poder seleccionar algún elemento mecánico con valores técnicos o comerciales, buscando siempre aquellos que cumplan con las especificaciones y sean seguros pero además que no estén demasiado sobrados en sus características, que resulten caros. Este problema permite seleccionar el tamaño comercial de un diámetro, por eso se eligió.
Motivación personal de cada integrante para seleccionar este problema
Samuel Esteban Gutiérrez Martínez:
Este problema me atrajo por su sencillez pero a la vez porque involucra bastantes conceptos para el diseño mecánico, como el límite elástico, esfuerzo máximo de diseño, esfuerzo máximo real, factor de seguridad y deformación elástica.
Planteamiento y descripción del problema
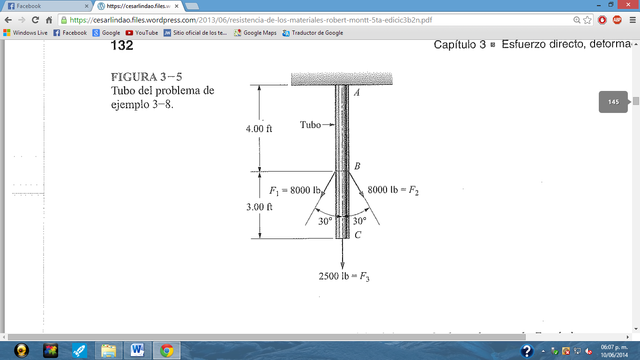
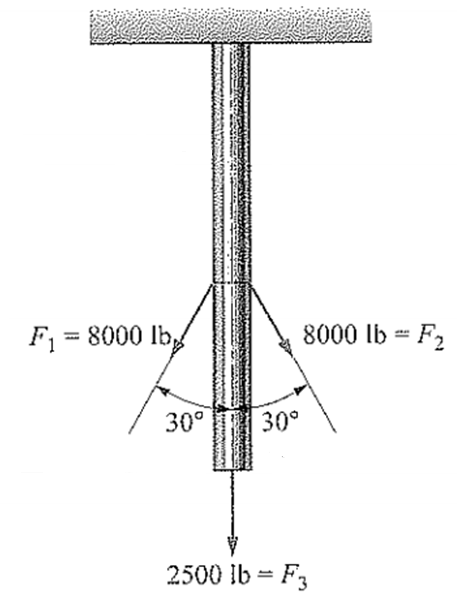
La figura presentada abajo muestra un tubo de acero utilizado para soportar un equipo mediante cables sujetos. Seleccione el tubo de acero cédula 40 más pequeño que limitara el esfuerzo a no más de 18 000 psi. Entonces, para el tubo seleccionado, determine la deflexión hacia abajo (estiramiento) en el punto C en la parte inferior del tubo conforme se aplican las cargas. Los elementos estarán en condiciones de temperatura ambiente a 20° C.
Objetivo
Seleccionar el tamaño comercial del tubo cedula 40 (valiéndose de la tabla A-12 proporcionada).
Determinar el alargamiento del tubo seleccionado.
Recalcular el esfuerzo máximo.
Obtener el factor de seguridad.
Y comparar los resultados analítico y computacional.
Datos
F1 = F2 = 8000 lb.
F3 = 2500 lb.
Sección A-B = 4 ft(12 in/ft)=48 in.
Sección B-C = 3 ft(12 in/ft)=36 in.
Esfuerzo máximo permisible, σ = 18 000 psi.
E = 30,000,000 psi
Limite elástico, Sy= 137895 KPa (librería NX) = 20,000 psi
Análisis
Primero hay que obtener el área del tubo para entonces seleccionarlo de la tabla A-12. Luego calcular la deformación provocada por cada fuerza y sumarla para obtener la deformación total.
A=F/σ
Las cargas que intervendrán son solo las axiales. Por lo que a las fuerzas F1 y F2 hay que descomponerlas para poder sumarlas con F3.
F Total axial=(2500+2(8000cos30°))lb =16,356.406 lb.
∴ A=(16,356.406 lb)/18,000psi=0.9089in2
Tomando el área inmediata superior con el área de 0.9089 in2 escogemos un tubo de 2 in de diámetro nominal:
Diámetro en in D externo en in D interno en in Área en in2
2 2.375 2.067 1.075
Con este nuevo valor de área podemos recalcular el esfuerzo máximo en Zz.
σZz=F/A=(16356.406lb/1.075in2)= 15,215.34 psi
Calculo de deformación
δ total = δ A-B + δ B-C
δ A-B = (F A-B)( L A-B)/(AE) = (16,356.406 lb)(48 in)/(1.075in¬-^2 )(30x〖10〗^6 lb/(in^2 )) =0.024344 in
δ B-C = (F B-C)( L B-C)/(AE) = (2500 lb)(36 in)/(1.075in¬^2 )(30x〖10〗^6 lb/(in^2 )) =0.002790 in
δ total = 0.024344 in+0.002790= 0.02790 in
Factor de seguridad
Este factor de seguridad es estimado ya que no toma en cuenta las fuerzas de 4000 libras que no son axiales.
FS = Sy/σmaxZz = 20,000 psi /15,215.34psi = 1.31
Planteamiento propuesto en NX
Material: Steel
Propiedades de la librería de NX:
======== Mecánico
Módulo de Young (E)
temperatura Youngs Modulus (E)
C mN/mm^2 (kPa)
20 206940000
======== Fuerza
Límite elástico
temperatura Límite elástico
C mN/mm^2 (kPa)
20 137895
Malla: Malla Tetraédrica de 10 nodos de tamaño de 0.5in
Fuerzas y empotramientos
Datos arrojados por NX:
Para plantear el problema realizamos la barra en Solidworks construyendo las 2 secciones para que marcara el borde en la sección intermedia. Y en NX después de mallar y dar material se pegaron los dos cuerpos con la herramienta gluing.
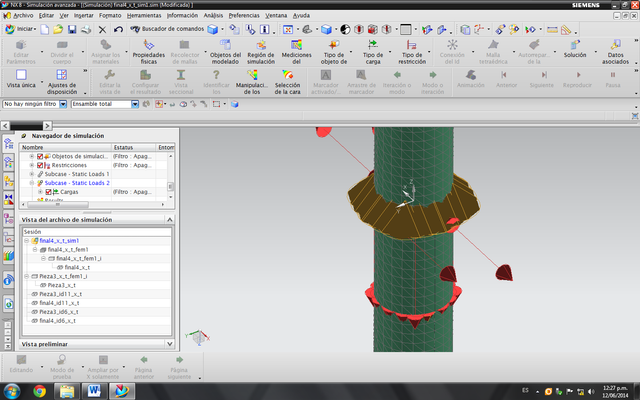
Aquí se pueden apreciar las componentes de las fuerzas en la sección intermedia y el pegado por gluing.
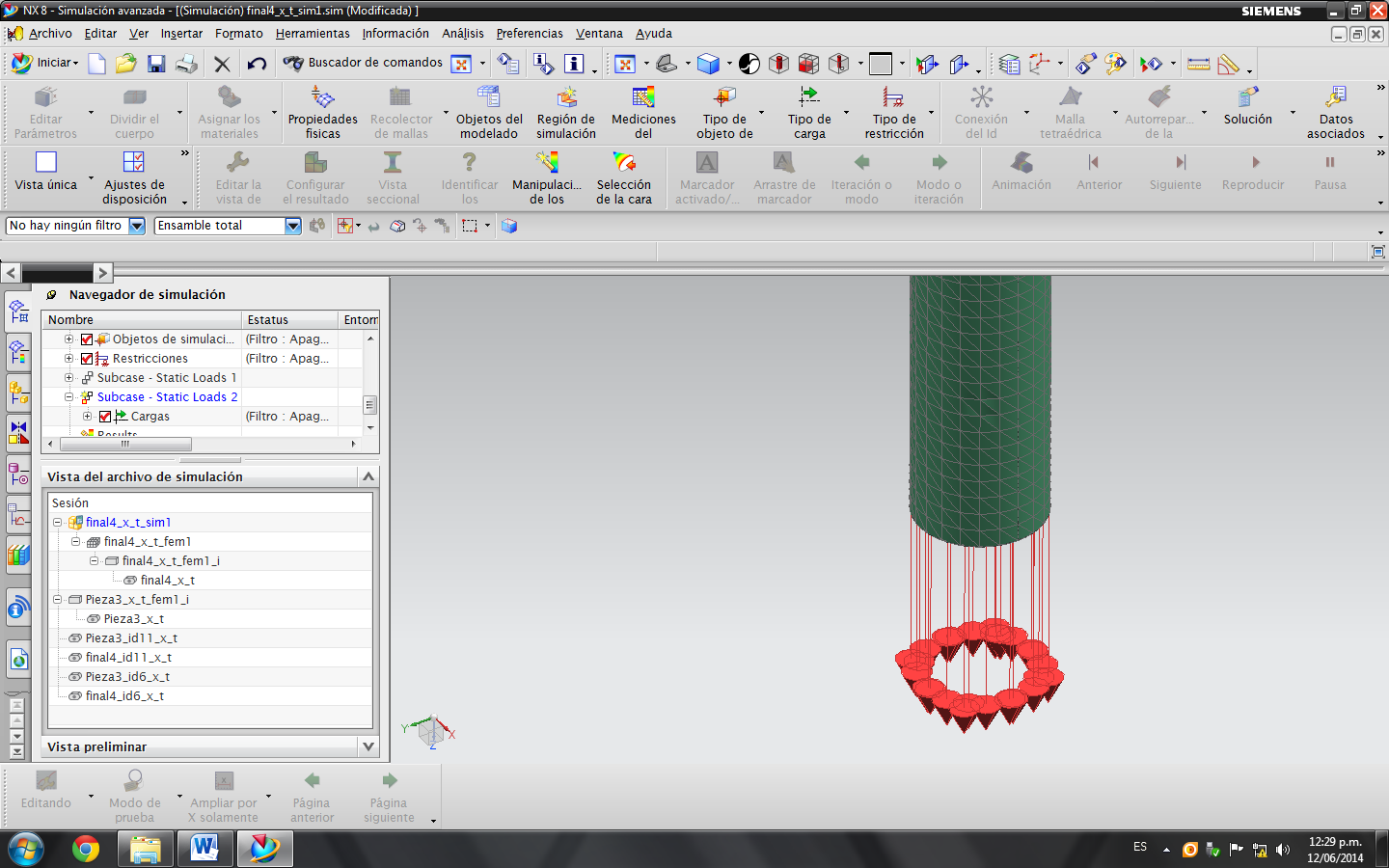
carga en la parte inferior
Deformación
Dato arrojado por NX: 0.0271 in.
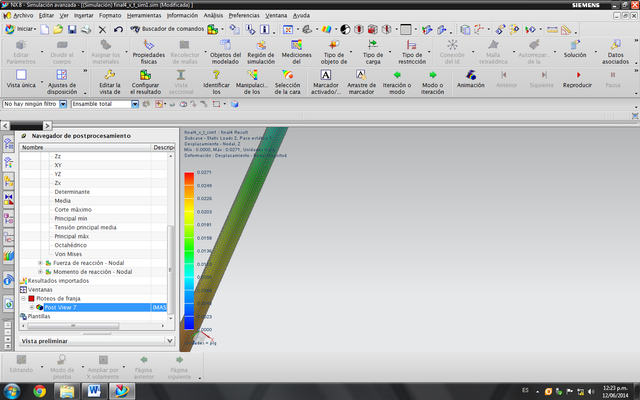
Comparación entre calculo analítico y con NX: 0.0279 in - 0.0271 in= 0.0008 in
Factor de seguridad con datos de NX
Y efectivamente las fuerzas axiales nos dicen la deformación, pero es una situación muy diferente con el esfuerzo máximo. Analíticamente calculamos este esfuerzo solo en dirección Zz (tomando en cuenta fuerzas axiales al tubo) pero con NX nos damos cuenta del esfuerzo real tomando en cuenta las fuerzas que no son axiales que también deforman el material.
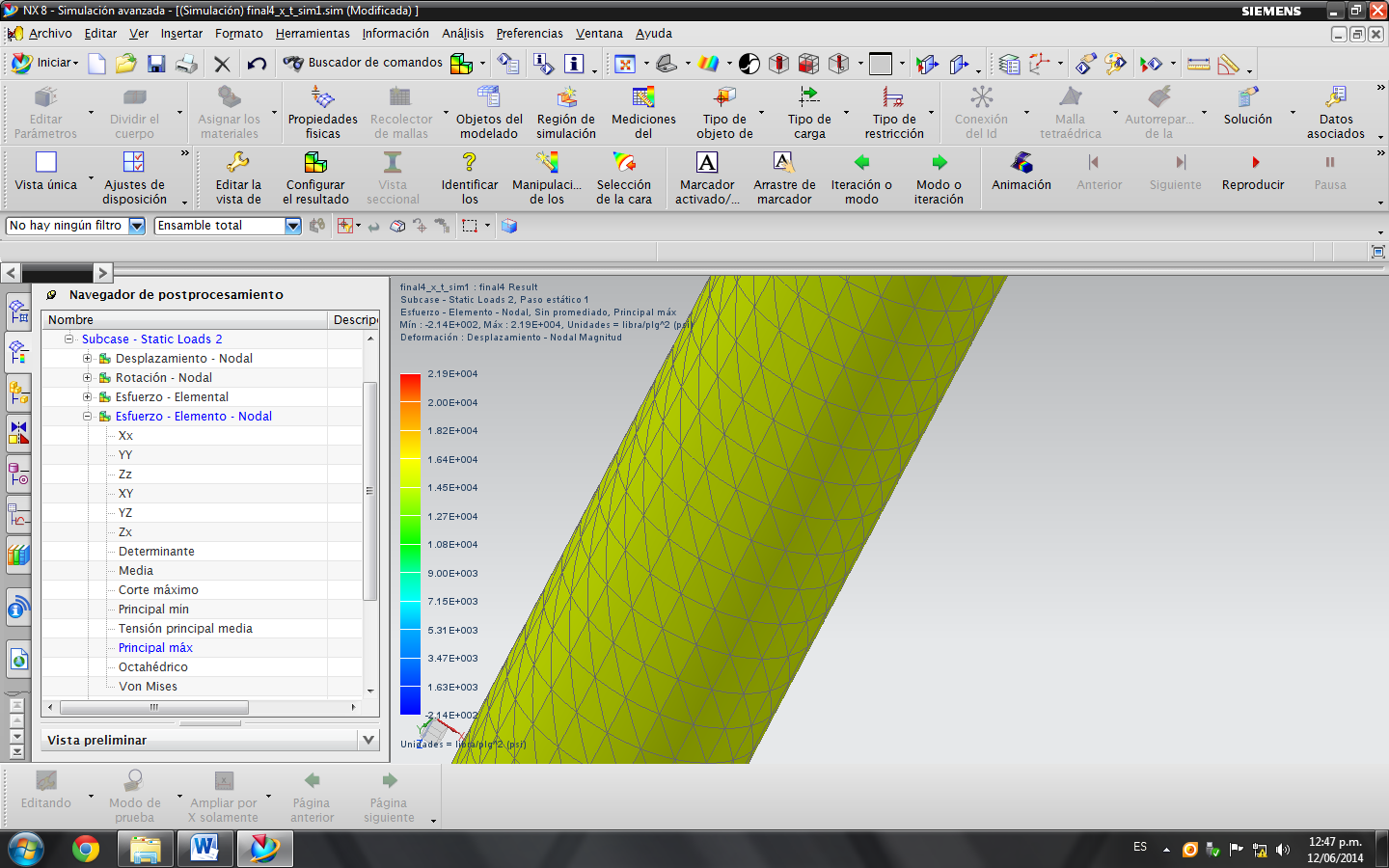
Esfuerzo principal
21900 psi
Esfuerzo principal
21900 psi
Fuentes de información
• Resistencia de materiales. Quinta edición de Robert L. Mott. Página 331
Se puede descargar de la siguiente página:
• Conversor de presión
http://online.unitconverterpro.com/es/conversion-de-unidad/conversor-alpha/pressure.html
• Librería de NX para propiedades de materiales.