6 Sigma: Les Fondamentaux
Les fondamentaux de Six Sigma : Statistiques statiques
Six sigma exploite de façon intense les outils statistiques pour collecter les données, les traiter, les analyser et produire les résultats. Les outils les plus utilisés constituent ce qu’on appelle les fondamentaux. Sans les étudier en profondeur dans ces pages, nous allons les énumérer et les expliquer au mieux.
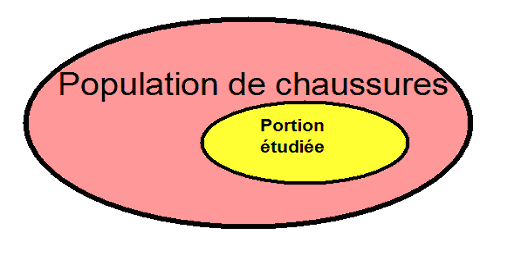
Dans la mise en œuvre de Six Sigma pour améliorer votre processus, vous allez toujours travailler sur des données : l’ensemble des chaussures que vous fabriquez, un groupe de clients, des services, des transactions, des documents, etc. Ces données constituent une population. Une population est donc l’ensemble des entités dont vous étudiez les caractéristiques.
En vue d’améliorer les performances de votre système de production, il peut arriver que vous décidiez d’étudier les produits que vous élaborez. Ce peut être mille paires de chaussures que vous fabriquez par jour. Comme il n’est pas facile d’analyser la qualité de chacune de ces chaussures, vous êtes obligés d’en étudier une petite portion seulement. C’est à cela que sert la statistique. Cette portion qui fait l’objet d’analyse doit être judicieusement sélectionnée afin qu’elle soit représentative de l’ensemble des chaussures que vous produisez, votre population de chaussures.
Lors de cette étude, deux grandeurs fondamentales décrivent vos données :
- Leur tendance centrale : moyenne, médiane, mode
- Leur variation ou dispersion autour de la valeur moyenne : écart-type.
Les plus utilisées sont la moyenne et l’écart-type (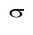
). Vous êtes habitués à la notion de moyenne.
L’écart-type permet d’estimer la variation, la dispersion de la population autour de la valeur moyenne. Elle mesure la distance se situant entre la moyenne et le point d’inflexion de la courbe normale. La mesure de l’écart-type permet de calculer / évaluer la capacité de votre processus.
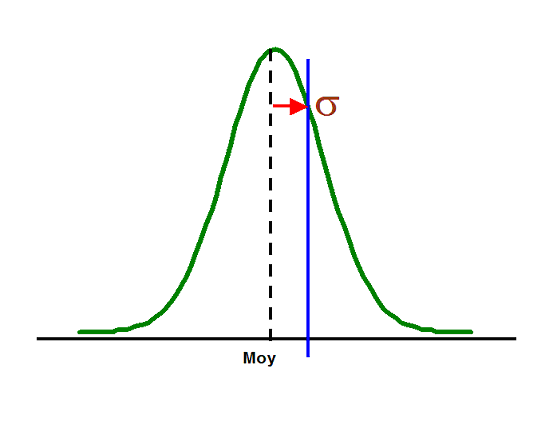
La statistique statique permet de savoir les performances de votre processus à tout moment.
Les distributions (ex. distribution normale) peuvent servir à estimer si une caractéristique est en deça ou au dessus des normes (ou limites).
Lorsque vous produisez une paire de chaussures (exemple pris au début), les dimensions, les coutures , etc. ne restent pas toujours identiques. Elles varient dans le temps. Il se produit des variations, ou dispersions. Pour améliorer votre processus de fabrication, vos devez réduire la variation en identifiant les principales causes qui contrôlent la moyenne et l’écart-type. Ceci pour ramener la moyenne à son niveau idéal. En faisant ainsi vous réduisez le nombre de défauts et augmentez votre rendement.