Les fractales
L’origine des fractales
Durant des siècles, la géométrie a été considérée comme simple et se limitait à des formes primaires, tels que les triangles, les cercles, les ellipses, etc…
Le maître de la géométrie de cette époque se nomme Euclide (300 av. J.C.). Il est l’auteur des célèbres ouvrages « les Eléments », qui présentaient des théorèmes de géométrie plane et solide ainsi que de l’arithmétique théorique.
Il faut attendre le XIXème siècle pour que ces formes « simples » soit reconsidérées par trois esprits « rebelles » :
Georg Cantor : un mathématicien allemand (1845-1918), connu pour être le créateur de la théorie des ensembles
Il est l’auteur de l’ensemble de Cantor
Wacław Franciszek Sierpiński : un mathématicien polonais (1882-1969), connu pour sa contribution à la recherche sur la théorie des ensembles, et plus particulièrement sur celle de l’Axiome du choix , de l’hypothèse de la continuité, mais aussi sur la théorie des nombres
Il est l’auteur du Triangle de Sierpinski
[Wikimedia]
Giuseppe Peano : un mathématicien italien (1858-1932), auteur de plus de 200 publications. Il s'est principalement intéressé aux mathématiques fondamentales, ainsi qu'à la théorie des langages.
Il est l’auteur de la Courbe de Peano
Grâce à leurs travaux qui s’étalent sur près d’un siècle, ces trois mathématiciens ont ouvert la voie à l’étude d'une nouvelle discipline mathématique…
Les fractales sont connues depuis le milieu du XXème siècle mais sont, à cette époque, considérées comme de simples curiosités géométriques.
C’est dans les années 70 qu’un mathématicien franco-américain d’origine polonaise, Benoît Mandelbrot (1924-2010) amène les fractales sur le devant de la scène.
Il en fait l'objet d'une nouvelle discipline mathématique que l’on nomme la géométrie fractale.
Mandelbrot invente lui-même le terme « fractale », issu du latin « fractus », qui signifie « brisé », afin de désigner un type d'objet dont l'irrégularité le distingue des figures géométriques euclidiennes telles que la droite ou le cercle.
Qu’est ce qu’une fractale ?
Il a fallu attendre l’arrivée des travaux de Mandelbrot afin de nous démontrer l’omniprésence des fractales, que ce soit dans la géométrie mais aussi dans la nature.
Voici l’exemple du « flocon de Koch », découvert par le mathématicien suédois Von Koch (1870-1924)
Il faut savoir que cette figure est apparue à l’époque comme une curiosité sans grand intérêt au sein du milieu scientifique….
1-) Prenons comme base un triangle équilatéral :
[Wikimedia]
2-) Remplacer le tiers central de chaque côté par deux segments de droite de longueurs égales à la partie retirée, comme sur la deuxième figure.
Répéter ainsi le processus, en remplaçant à chaque fois le tiers central de chaque côté.
[Pixabay]
Le flocon de Koch est ce que l’on obtient lorsque l’opération a été répétée une infinité de fois.
[Wikimedia]
Ce flocon possède des particularités remarquables :
- Si l’on zoome sur cette figure à l’aide d’un microscope, on se rend compte que le même motif se répète indéfiniment à des échelles de plus en plus petites.
La première propriété des fractales est que leur structure ne change pas lorsque l’on modifie l’échelle.
C’est ce que l’on nomme l'invariance d’échelle
- La courbe qui compose le contour du flocon a pour particularité d’être de longueur infinie, alors même que l’aire qu’elle délimite est quant à elle finie.
On a donc une surface de taille connue, entourée par un périmètre de longueur infinie !
On observe la même chose concernant les côtes littorales bretonnes. En effet, si l’on mesure de façon grossière, avec des instruments dont la résolution est de 100 km, on obtiendra une longueur de côte d’environ 500 km.
Mais avec une précision de 1 km, le périmètre s’affine et la mesure rentre dans la rugosité de la côte de façon plus précise, ce qui nous donne un périmètre de 5 000 km !
Ainsi, si nous voulons aller plus loin, si l’on réitère l’opération, avec une précision de 10 mètres, on obtient une longueur de côtes de plusieurs dizaines de milliers de kilomètres !
Plus la précision augmente, plus la longueur augmente.
On peut donc considérer que les côtes bretonnes ont une longueur infinie !
Le littoral breton, la forme des roches mais aussi des arbres, des nuages présentent un aspect fractal.
Mandelbrot nous révèle le monde comme nous ne l’avons jamais vu, en discernant dans le chaos apparent une certaine régularité très précise de la nature.
Les Fractales : la 1,26ème dimension
Il est courant de dire que le monde qui nous entoure est en 3 dimensions.
Et pour caractériser ces dimensions, il est d’usage de les représenter par des figures géométriques :
La dimension zéro :
Une figure de dimension 0 est représentée par un simple point.
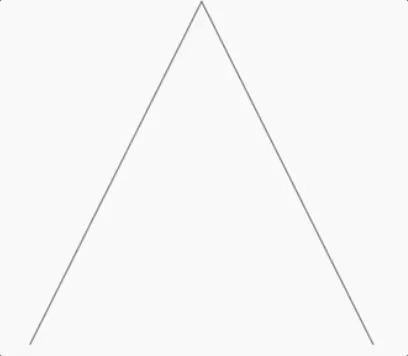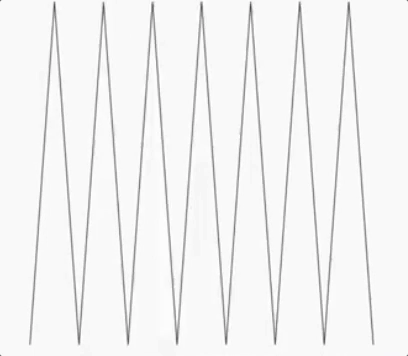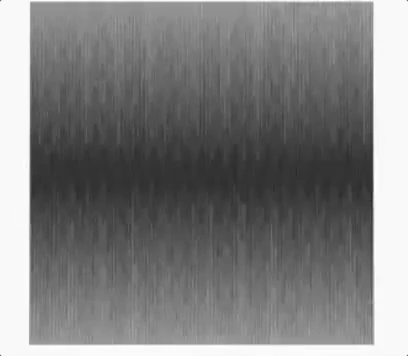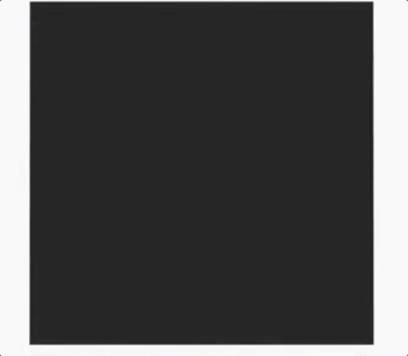
La première dimension :
Une figure qui possède une seule dimension se représente par une ligne.
Même si théoriquement, les lignes ne devraient pas avoir d’épaisseur, on considèrera que l’épaisseur de l’encre déposée par le stylo est négligeable.
La deuxième dimension :
La deuxième dimension est celle des surfaces.
Il faut cependant savoir qu’une figure en 2D n’est pas forcément plane, elle peut être tordue et incurvée dans l’espace.
La troisième dimension :
La troisième dimension représente la catégorie des volumes.
Pensez-vous que toutes les figures géométriques peuvent être classées dans ces 3 seules dimensions ?
Et bien aussi étonnant que cela puissent paraitre, les fractales se classent parmi les figures géométriques intermédiaires.
En effet, les fractales ne sont pas définies par une dimension dont le nombre est entier (1,2 ou 3), mais par un nombre à virgule !
Reprenons l’exemple du flocon de Koch :
Quelle est la longueur de la courbe de Von Koch ?
Comme vu précédemment, à chaque étape de la construction du flocon de Koch, nous avons découpé chaque segment en 3 tiers puis nous lui avons enlevé un tiers et ajouté 2 segments de longueur un tiers.
En clair, cela revient à dire que la longueur de la courbe subit une augmentation de 33% à chaque étape de sa construction.
La courbe augmente donc de longueur autant de fois que le processus est répété, et par conséquent sa longueur est infinie, sachant que paradoxalement la surface du flocon de Koch quand à elle est finie.
La question que l’on peut se poser est la suivante :
Peut-on définir la courbe de Van Koch par une ligne en 1 dimension ?
A partir de ce procédé qui consiste à répéter une infinité d’étapes caractérisant les fractales, il est tout à fait possible de produire des surfaces avec des lignes en une dimension.
Voici un exemple :
Cette figure au départ est composée de 2 segments, puis on augmente leur nombre par 4 segments, puis 6, puis 8 etc… de façon à les augmenter à l’infini.
On peut donc constater qu’à partir d’une figure à une seule dimension, on obtient une surface à 2 dimensions (un carré).
De la même façon, la courbe de Van Koch, à force de s’entortiller sur elle-même, finira par remplir des bandes de surface.
Pour résumer, la courbe de Von Koch est une figure géométrique intermédiaire se situant entre la dimension 1 et 2.
Ainsi, de la même manière qu’il est concevable de mesurer les lignes par leurs longueurs ou les surfaces par leurs airs, il est possible de calculer les figures de dimension intermédiaire par des mesures que l’on appellent les dimensions de Hausdorff-Besicovitch du nom des mathématiciens Felix Hausdorff et Abram Besicovitch.
La courbe de Von Koch aura donc une mesure qui ne sera ni en mètre ni en mètre carré, mais en mètre puissance 1,26.
1,26 représente la dimension fractale qui caractérise la complexité d’un objet.
Le littoral breton possède une dimension fractale d’environ 1,26 comme la courbe de Von Koch. Un nuage quant à lui a une dimension de 1,35.
Plus l’échelle tend vers 1 et plus l’objet est lisse, tandis qu’une dimension tendant vers 2 implique une complexité fractale croissante.
A l’époque, la dimension de Hausdorff-Besicovitch n’avait qu’une existence théorique, jusqu’à ce que Mandelbrot l’utilise pour ses propres recherches.
Mandelbrot a été visionnaire en se rendant compte que c’était un outil parfait pour décrire l’irrégularité de la nature.
L’omniprésence des fractales
Elles sont présentes partout, et bien évidemment, avant toute chose, dans la nature.
En biologie, on les considère comme des schémas que la nature reproduit sans cesse au fil de l’évolution.
L’arbre qui cache la forêt
Les arbres sont de très bons exemples de fractales autosimilaires.
En effet, lorsque l’on observe les embranchements, on s’aperçoit que leur schéma structurel est semblable pour l’ensemble de l’arbre. On distingue des branches mères qui se divisent en branches plus petites.
Si on observe les ramifications, on remarque que le schéma est le même et se répète sur l’ensemble des branches jusqu’aux extrémités des feuilles.
De la même manière qu’une forêt peut sembler aléatoire et chaotique, des études prouvent que l’implantation des arbres d’une forêt correspond à un cahier des charges très précis, établi dans la structure même des arbres présents dans la forêt.
Ce qui tend à prouver qu’une forêt possède une structure non aléatoire mais une implantation très ordonnée, suivant une harmonie fractale.
Le Chou Romanesco
Le chou Romanesco, qui en plus d’être excellent pour la santé, possède une des plus belles preuves de particularité fractales.
Chaque partie du chou, de la plus petite à la plus grande, possède une forme qui correspond aussi à la forme de l'ensemble de la plante : un modèle parfait d’autosimilarité.
L’utilité des fractales
Aujourd’hui, les fractales permettent diverses applications dans de nombreux domaines scientifiques.
En plus de leur indéniable utilité, elles permettent d'ouvrir de nouvelles perpectives de recherches.
Les murs antibruit
Les nuisances sonores sont une source de pollution majeure dans nos villes.
En partant de cette constatation, des chercheurs du CNRS ont eu l’idée de construire des murs antibruit s’inspirant des propriétés géométriques des fractales.
Le résultat est plus que probant : une réduction de plus de 60% du niveau sonore comparé à un mur antibruit classique !
L’idée leur est venue suite à l’observation des côtes bretonnes.
En effet, le littoral possède une forme fractale qui lui permet d’absorber la puissance des vagues qui viennent y déferler.
Comme vu précédemment, les contours des côtes rocheuses ont une longueur que l’on peut considérer comme virtuellement infinie.
Ainsi, avec un grand nombre de surfaces de contact, les ondes finissent par s’amortir et réduisent ainsi la force des vagues.
Il en est de même pour les ondes sonores qui ne sont finalement que des vagues se propageant dans l’air.
Il serait donc logiquement possible de créer des digues de structure fractale qui pourraient diminuer la destruction des falaises, ou d’atténuer la force des vagues sur certains littoraux agités.
Les antennes fractales
Dans notre société où la télécommunication est au centre de toute notre attention, les exigences de miniaturisation sont en constante augmentation.
A l’heure actuelle, nous possédons tous des appareils utilisant des antennes de réception Gps, Bluetooth, Wifi etc.. Mais chacune d’entre elles nécessite une bande de fréquence différente.
Il fallait donc trouver une solution afin d’éviter d’avoir plusieurs antennes sortant des appareils mobiles.
La solution est simple, il suffit d’observer les plantes.
En effet, en pliant une antenne à la manière du flocon de Koch (en diminuant la longueur à chaque fractionnement), il est possible d’améliorer la puissance et la qualité de réception.
Non seulement le gain de place est drastiquement amélioré, mais il est également possible de capter des fréquences différentes avec une même antenne, en rajoutant simplement des branches ainsi que des ramifications, telle une plante !
Conclusion
Ces formes étranges sont omniprésentes dans la nature, et autour de nous, dans notre corps, mais aussi dans la recherche médicale, les jeux vidéos, les télécommunications, la bourse etc…
Les exemples sont nombreux, voir même encore une fois…infini !
Les travaux de Benoît Mandelbrot ont permis de rationaliser des formes qui nous semblaient avant cela chaotiques.
Mais alors pourquoi la nature utilise-t-elle les fractales ? Benoît Mandelbrot apporte la réponse : pour faciliter les échanges tout simplement.
En effet, il a réussi a prouver que les fractales avaient, pour un volume fini, un périmètre infini offrant une surface de contact immensément grande.
Grâce à Mandelbrot, les côtes maritimes, les nuages, les montagnes… Le monde qui nous entoure, possède bel et bien une logique mathématique. Il nous a ouvert les yeux et nous a permis d’élargir encore plus notre connaissance de l'univers…
Enfin, les chercheurs estiment que l'étude des fractales n'a pas encore livré tous ses secrets. C’est une science jeune qui nous réserve quelques surprises dans l'avenir.
A savoir :
Contrairement à la croyance, le mot "fractal" est masculin.
Benoît Mandelbrot tenait à cette exception à la règle des pluriels en "aux", comme les festivals, les chacals etc…
Une grande partie de la communauté scientifique n'a pas perçu cette subtilité et, entendant le pluriel "fractals" en a déduit de façon erronée qu'il s'agissait d'un féminin.






Article impressionnant, bravo !
Super démonstration ! je connais un peu les fractales mais là tu viens de nous fournir un éclairage tout nouveau. Les petites vidéos sont tout bonnement renversantes et nous rendent un peu dingues à la longue. Félicitations @yann85.
Hello! This post is very interesting. Why did not you post new posts for a long time?
Thanks for subscribing to my blog, it's mutual. I wish you creative mood!
Un sujet magnifiquement traité. Je trouve même qu'il y a de poésie dans la façon dont tu l'as abordé. Je pense aux fractales à chaque fois que j'achète un chou romanesco mais je ne pensais pas que l'on pouvait aller plus loin. Un grand article !👍
Le sujet m'a toujours beaucoup intéressé !
Mais alors là !! Faire une relation entre la côte bretone et les fractales, je dis bravo, chapeau bas 😄😄
Très bon article 👍
Un seul mot : impressionné. Où donc vas tu chercher tes sujets ? Dis le moi où je te downvote 😂😂😂😂
Merci ! C'est la Bretagne qui m'inspire ! Ici on capte mal, on mange du choux, et la cote sauvage est à 100 mètre . Voilà t'as les 3 sujets loool
😂😂
Impressionnant comme toujours ! bravo !
Merci c'est remarquable !
C'est hypnotisant ! Tes gif m'ont donné mal à la tête haha ! C'est incroyable, merci de m''avoir fait découvrir ! :)
Oui ! faut pas les regarder trop longtemps ;-)
Merci pour ton commentaire @whentone
INFINIMENT hypnotisant... MERCI Yann pour cet article dans lequel on plonge en spirale.