13-11-2024 - Education - Linear Algebra - Linear Applications and Matrices [EN]-[IT]

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
[ENGLISH]
13-11-2024 - Education - Linear Algebra - Linear Applications and Matrices [EN]-[IT]
With this post I would like to provide some brief notions regarding the technical topic mentioned in the subject.
The context in which we operate is that of analytical geometry or linear algebra
(code notes: MOD-78)
Linear Applications and Matrices
A matrix associated with an application represents the linear transformation to which it refers with respect to two fixed bases of the starting and ending vector spaces. This matrix provides the information relating to the transformation to which it is associated, therefore it plays a leading role in the field of linear applications.
There is a general method to determine the matrix associated with any linear application. This method then allows us to analyze in detail the cases in which the linear transformation is assigned in explicit form or through images of domain vectors.
Definition of representative matrix
In order to give the definition of representative matrix of a linear transformation we can continue as follows.
Let us consider two vector spaces V,W defined on the same field K and with dimensions n,m respectively.
Let us consider a linear application 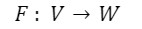 and let CE43Fve9VvYTcEhyd9r/image.png) respectively a basis of the vector space V and one of W The matrix associated with the linear application
and let CE43Fve9VvYTcEhyd9r/image.png) respectively a basis of the vector space V and one of W The matrix associated with the linear application 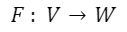 with respect to the bases Bv and Bw
with respect to the bases Bv and Bw
can be constructed in the following way
Determine the image
We can start by determining the image with respect to the application F of each vector vi of the bases Bv and Bw
We then calculate
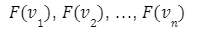
Linear combinations
The vectors obtained are elements of W and can therefore be expressed as a linear combination of the basis vectors Bw of the space W. Below are the elements expressed as a linear combination.
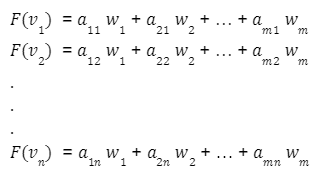
Associated matrix
The matrix that has for j-th column the vector of the coordinates of the image F(vj) with respect to the base of W is called the matrix associated to the linear application F with respect to the bases Bv and Bw.
The matrix will be indicated as follows
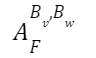
This term is read as A which is the matrix associated to the linear application F with respect to the bases Bv and Bw.

We can also say that the matrix associated with a linear application
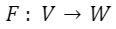
compared to the bases
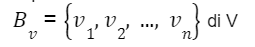
and
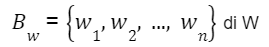
is that matrix whose columns are the coordinates with respect to the arrival base Bw of the images according to F of the vectors of the starting base Bv.
Conclusions
In conclusion we can say that linear applications of matrices are mathematical transformations that act on vectors within a vector space, respecting linearity properties: that is, they preserve the sum of the vectors and the multiplication by scalars.
Question
Have you ever tried to do linear applications on matrices?

[ITALIAN]
13-11-2024 - Education - Algebra lineare - Applicazioni lineari e matrici [EN]-[IT]
Con questo post vorrei fornire alcune brevi nozioni a riguardo dell’argomento tecnico citato in oggetto.
Il contesto in cui operiamo è quello della geometria analitica o algebra lineare
(code notes: MOD-78)
Applicazioni lineari e matrici
Una matrice associata ad un’applicazione rappresenta la trasformazione lineare cui è riferita rispetto a due fissate basi degli spazi vettoriali di partenza e d’arrivo. Questa matrice fornisce le informazioni relative alla trasformazione cui è associata, dunque riveste un ruolo da protagonista nell’ambito delle applicazioni lineari.
Esiste un metodo generale per determinare la matrice associata ad un’applicazione lineare qualsiasi. Questo metodo permette poi di analizzare nel dettaglio i casi in cui la trasformazione lineare è assegnata in forma esplicita oppure mediante immagini di vettori dominio.
Definizione di matrice rappresentativa
Al fine di dare la definizione di matrice rappresentativa di una trasformazione lineare possiamo proseguire come segue.
Consideriamo due spazi vettoriali V,W definiti sullo stesso campo K e di dimensioni rispettivamente pari a n,m.
Consideriamo un’applicazione lineare
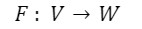
e siano
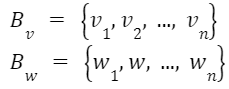
rispettivamente una base dello spazio vettoriale V e una di W
La matrice associata all’applicazione lineare
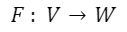
rispetto alle basi Bv e Bw
si può costruire nel seguente modo
Determinare l’immagine
Possiamo iniziare determinando l’immagine rispetto all’applicazione F di ogni vettore vi delle basi Bv e Bw
Calcoliamo quindi
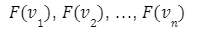
Combinazioni lineari
I vettori ottenuti sono elementi di W e possono quindi essere espressi come combinazione lineare dei vettori base Bw dello spazio W. Qui di seguito gli elementi espressi come combinazione lineare.
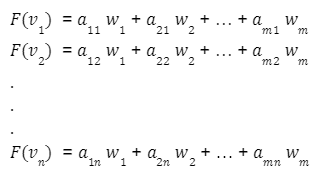
Matrice associata
La matrice che ha per j-esima colonna il vettore delle coordinate dell’immagine F(vj) rispetto alla base di W si dice matrice associata all'applicazione lineare F rispetto alle basi Bv e Bw.
La matrice verrà indicata come segue
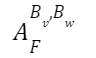
Questa dicitura si legge come A che è la matrice associata all’applicazione lineare F rispetto le basi Bv e Bw.

Possiamo dire anche che la matrice associata a un’applicazione lineare
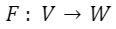
rispetto alle basi
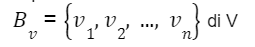
e
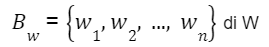
è quella matrice che ha per colonne le coordinate rispetto alla base d’arrivo Bw delle immagini secondo F dei vettori della base di partenza Bv.
Conclusioni
In conclusione possiamo dire che le applicazioni lineari di matrici sono trasformazioni matematiche che agiscono su vettori all'interno di uno spazio vettoriale, rispettando proprietà di linearità: cioè, preservano la somma dei vettori e la moltiplicazione per scalari.
Domanda
Avete mai tentato di fare delle applicazioni lineari su matrici?
THE END
Education is really vital and should not be joked with right now. We need to pay close attention to and make sure and that is what I love so
I consider this type of education as gymnastics for our brain.
Sì, l'ho fatto, presenti ogni operazione molto bene nel post, molto organizzato, facile da capire
grazie per aver lasciato un commento. Ogni volta che scrivo un articolo di questo genere mi rendo conto che avrei potuto spiegarlo meglio, ma mi fa piacere che tu abbia compreso
Aspetto un post con la tua musica.
Ti auguro una notte felice
hai ragione è da un po' di tempo che non faccio un post sui miei brani musicali. Mi hai dato una buona idea.
This post has been upvoted by @italygame witness curation trail
If you like our work and want to support us, please consider to approve our witness
Come and visit Italy Community
Hi @stefano.massari,
my name is @ilnegro and I voted your post using steem-fanbase.com.
Come and visit Italy Community