19-11-2024 - Education - Linear Algebra - Mutual Position [EN]-[IT]

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
[ENGLISH]
19-11-2024 - Education - Linear Algebra - Mutual Position [EN]-[IT]
With this post I would like to provide some brief notions about the technical topic mentioned in the subject.
The context in which we operate is that of analytical geometry or linear algebra
(code notes: MOD-69)
Mutual position of affine subspaces
The mutual position of affine subspaces is quite similar to that of vector subspaces.
Let's recall the concept of a vector subspace. In analytical geometry and linear algebra, a vector subspace is a subset of a vector space that is itself a vector space with respect to the operations of vector addition and scalar multiplication defined in the original space.
There is an important difference between affine subspaces and vector subspaces in fact contrary to what happens with vector subspaces, affine subspaces may not intersect.
Notation
Two affine subspaces S1 and S2 are said to be coincident if S1=S2
Definition
Two affine subspaces S1 = P1+W1 and S2 = P2+W2 are said to be parallel if
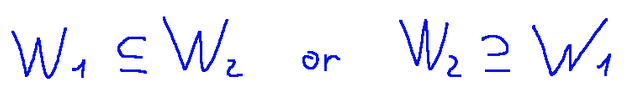
Note:
The following writing means that J is a subset of I
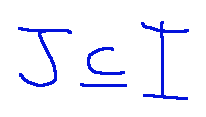
In analytic geometry, the mutual position of affine subspaces describes how two affine subspaces "relate" or "intersect" in space. This relationship is based on their dimension, their direction (i.e. the associated vector subspaces), and the relative position of the points that define them.
Formally, an affine subspace A can be written as:
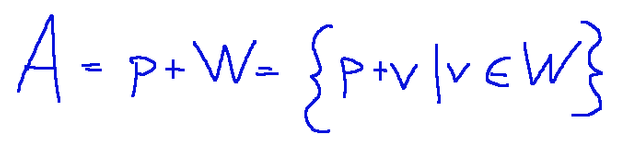
Example
Let's try to find the mutual position of the following pair of lines of V 2 G, defined with implicit or parametric forms.
(x + 2Y -1 = 0) and (3x - y -2 = 0)
The lines are implicitly defined as:
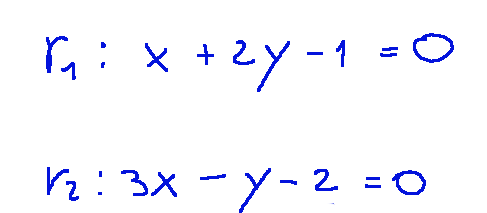
1-Calculation of directional vectors
The lines are expressed in implicit form ax+by+c=0, so the normal vectors are:
For r1: the normal vector n1 = (1,2)
For r2: the normal vector n2 = (3,-1)
The directional vectors of the lines are orthogonal to the normal vectors:
For r1: v1 = (-2,1)
For r2: v2 = (1,3)
2-Comparison of directional vectors
In this phase Let's determine whether the lines are parallel or not by checking whether the vectors v1 and v2 are proportional:
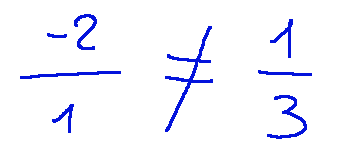
Since the directional vectors are not proportional, therefore the lines are not parallel. This implies that the lines intersect.
3-Calculating the point of intersection
To find the point of intersection we must solve the system formed by the two equations.
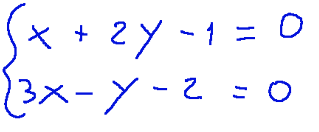
Calculation procedure

We proceed with the calculation of y by substituting x
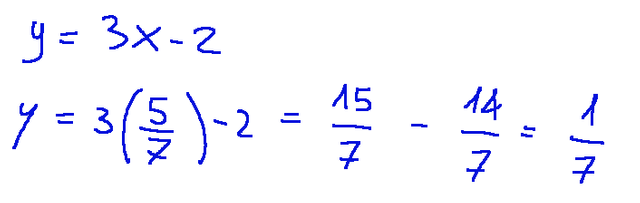
Now we know the point of intersection is
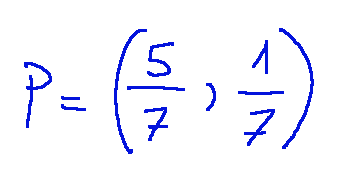
Result
The lines r1 and r2 are incident, that is, they intersect and the point of intersection is P = (5/7,1/7)
Conclusions
In conclusion we can summarize the following. The mutual position of affine subspaces describes how two affine subspaces relate or intersect in space.
Question
Do you remember studying these concepts in school?

[ITALIAN]
19-11-2024 - Education - Algebra lineare - Mutua posizione [EN]-[IT]
Con questo post vorrei fornire alcune brevi nozioni a riguardo dell’argomento tecnico citato in oggetto.
Il contesto in cui operiamo è quello della geometria analitica o algebra lineare
(code notes: MOD-69)
Mutua posizione di sottospazi affini
La mutua posizione dei sottospazi affini è abbastanza simile a quella dei sottospazi vettoriali.
Ricordiamo il concetto di un sottospazio vettoriale. In geometria analitica e algebra lineare, un sottospazio vettoriale è un sottoinsieme di uno spazio vettoriale che è esso stesso uno spazio vettoriale rispetto alle operazioni di somma vettoriale e moltiplicazione scalare definite nello spazio originale.
Tra sottospazi affini e sottospazi vettoriali c'è una differenza importante infatti contrariamente a quanto succede con i sottospazi vettoriali, i sottospazi affini possono non intersecarsi.
Notazione
Due sottospazi affini S1 e S2 sono detti coincidenti se S1=S2
Definizione
Due sottospazi affini S1 = P1+W1 e S2 = P2+W2 sono detti paralleli se vale
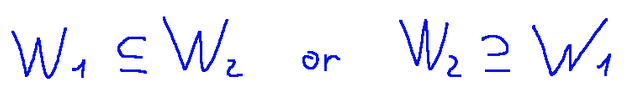
Note:
La seguente scrittura significa che J è un sottoinsieme di I
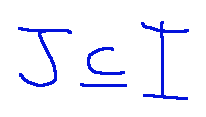
In geometria analitica, la mutua posizione di sottospazi affini descrive come due sottospazi affini si "relazionano" o si "intersecano" nello spazio. Questa relazione si basa sulla loro dimensione, sulla loro direzione (ossia i sottospazi vettoriali associati) e sulla posizione relativa dei punti che li definiscono.
Formalmente, un sottospazio affine A può essere scritto come:
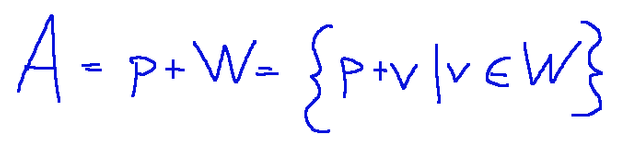
Esempio
Proviamo a trovare la mutua posizione della seguente coppia di rette di V 2 G, definite con forme implicite o parametriche.
(x + 2Y -1 = 0) e (3x - y -2 = 0)
Le rette sono definite implicitamente come:
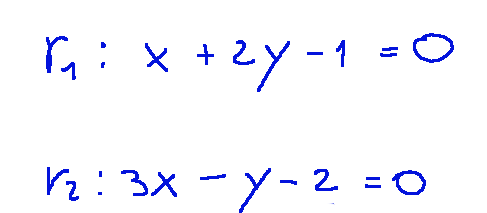
1-Calcolo dei vettori direzionali
Le rette sono espresse in forma implicita ax+by+c=0, per cui i vettori normali sono:
Per r1: il vettore normale n1 = (1,2)
Per r2: il vettore normale n2 = (3,-1)
I vettori direzionali delle rette sono ortogonali ai vettori normali:
Per r1: v1 = (-2,1)
Per r2: v2 = (1,3)
2-confronto dei vettori direzionali
In questa fase determiniamo se le rette sono parallele o meno andando a verificare se i vettori v1 e v2 sono proporzionali:
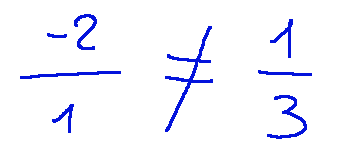
Siccome i vettori direzionali non sono proporzionali, quindi le rette non sono parallele. Questo implica che le rette si intersecano.
3-Calcolo del punto di intersezione
Per trovare il punto di intersezione dobbiamo risolvere il sistema formato dalle due equazioni.
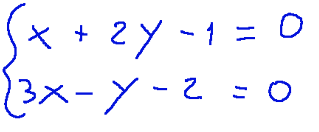
Procedura di calcolo

Procediamo con il calcolo di y sostituendo x
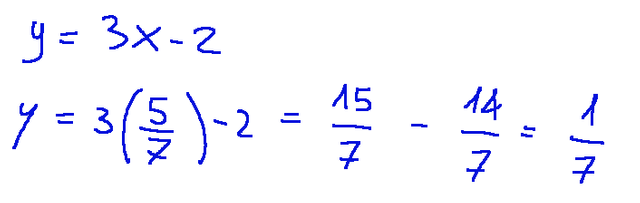
Ora sappiamo che il punto di intersezione è
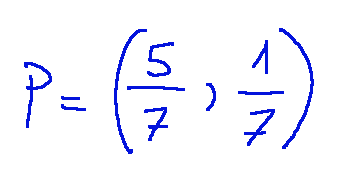
Risultato
Le rette r1 e r2 sono incidenti, cioè si intersecano e il punto di intersezione è P = (5/7,1/7)
Conclusioni
In conclusione possiamo sintetizzare quanto segue. La mutua posizione di sottospazi affini descrive come due sottospazi affini si relazionano o si intersecano nello spazio.
Domanda
Ricordate di aver studiato questi concetti a scuola?
THE END
Thank you so much for always taking adequate of your time to explain that which we need to understand and also helping to explain it in a much more better way for us to actually understand. Thank you for this piece of information
0.00 SBD,
0.64 STEEM,
0.64 SP
Thanks for leaving a comment. Linear algebra may seem easy to understand at first, but the deeper you delve into the subject, the more complicated it gets, and this complication always increases throughout the entire field of linear algebra. At least in my opinion.
Algebra lineare, ho visto la materia, ho studiato con alcuni compagni di classe, ricordo che SANTIAGO ha imparato subito, eravamo un gruppo di 5 compagni di classe, ci aiutavamo a vicenda, ma SANTIAGO era il più intelligente, attualmente hanno una loro azienda, ci incontravamo ancora per bere qualche drink
0.00 SBD,
0.09 STEEM,
0.09 SP
La prima parte dell'algebra lineare la capisco, poi fatico a comprendere invece tutta l'altra parte. Grazie che ci hai raccontato la storia del tuo amico. Evidentemente era intelligente ed ha saputo sfruttare questa sua caratteristica creando un impresa. Per quanto mi riguarda, metà dell'algebra lineare non la comprendo, quindi probabilmente non ho le capacità di fare impressa, oppure diciamo che è meglio che non mi assuma il rischio.
0.00 SBD,
0.52 STEEM,
0.52 SP
Ammetto che a scuola non abbiamo mai trattato questi argomenti così complessi ma questo post esplicativo si capiscono un po’ di nozioni !
Anche se sarebbe meglio avere nozioni basilari più solide
Grazie per la condivisione di informazioni 🙋♀️
0.00 SBD,
0.06 STEEM,
0.06 SP
grazie per essere passato di qua. L'algebra lineare ad un certo punto si fa complessa, ed io dico che non è per tutti... ma quando dico che non è per tutti, intendo per tutti gli insegnanti. Io stesso dopo che ho scritto questo post mi sono accorto che avrei potuto fare di meglio ed ho ommesso di spegnare alcune cose importanti.
0.00 SBD,
0.02 STEEM,
0.02 SP