24-11-2024 - Education - Linear Algebra - Projective Spaces [EN]-[IT]

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
[ENGLISH]
24-11-2024 - Education - Linear Algebra - Projective Spaces [EN]-[IT]
With this post I would like to provide some brief notions about the technical topic mentioned in the subject.
The context in which we operate is that of analytical geometry or linear algebra
(code notes: MOD-61)
Projective Spaces
Projective geometry is useful for studying curves and surfaces.
Projective spaces are a fundamental concept of analytical and algebraic geometry and are used to extend Euclidean space. They are also used to study geometric properties in a more general way.
Projective geometry is based on perspective. For example, it formalizes the fact that two parallel lines (for example, railroad tracks) seem to meet at some point. This point will be called the point at infinity, in fact it cannot be reached, so it seems to be at a finite distance.
Projective line
The projective line
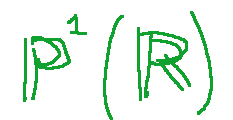
is the quotient set of the set
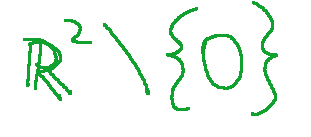
for the given equivalence relation ~ from

if and only if
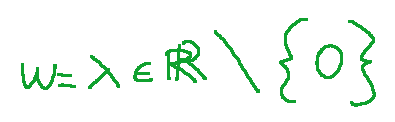
Consideration
The point
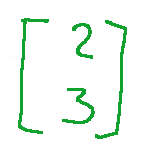
Of
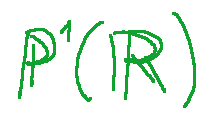
can also be represented by
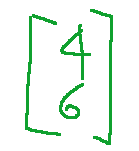
and
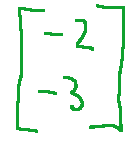
that is, we have that
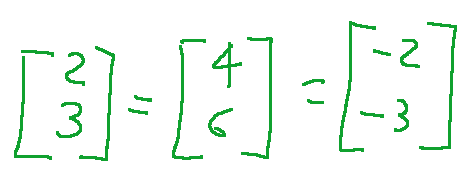
Definition of projective space
A projective space
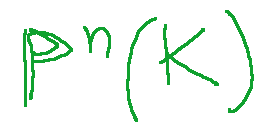
defined on a field K is the set of lines passing through the origin in the vector space
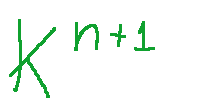
Each point of the projective space corresponds to a direction in the space vector
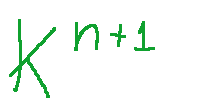
Formally we have the following writing
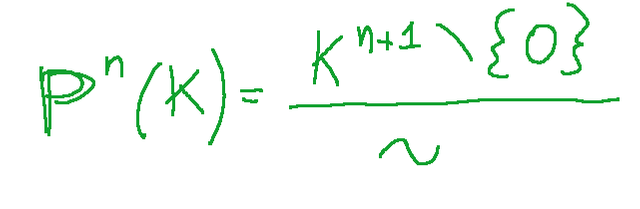
Conclusions
Projective spaces represent a natural extension of affine spaces that allows us to study geometry in a more complete and general way. Introduced to solve problems such as parallelism and to unify the treatment of points "at infinity", these spaces offer a rich and powerful mathematical structure.
Question
Have you ever studied projective spaces at school?

[ITALIAN]
24-11-2024 - Education - Algebra lineare - Spazi proiettivi [EN]-[IT]
Con questo post vorrei fornire alcune brevi nozioni a riguardo dell’argomento tecnico citato in oggetto.
Il contesto in cui operiamo è quello della geometria analitica o algebra lineare
(code notes: MOD-61)
Spazi proiettivi
La geometrica proiettiva è utile per studiare le curve e le superfici.
Gli spazi proiettivi sono un concetto fondamentale della geometria analitica e algebrica e vengono utilizzati per estendere lo spazio euclideo. Con essi si studiano anche le proprietà geometriche in modo più generale.
La geometria proiettiva è basata sulla prospettiva. Ad esempio, formalizza il fatto che due rette parallele (esempio i binari della ferrovia) sembrano incontrarsi in un qualche punto. Questo punto sarà detto punto all’infinito, infatti non può essere raggiunto, quindi sembra essere a una distanza finita.
Retta proiettiva
La retta proiettiva
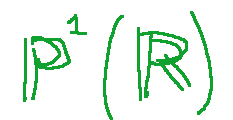
è l’insieme quoziente dell’insieme
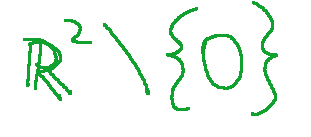
per la relazione di equivalenza ~ data da

se e solo se
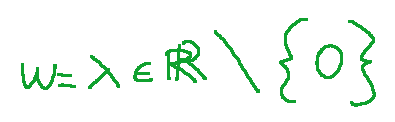
Considerazione
Il punto

di
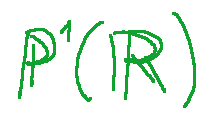
può essere anche rappresentato da

e

ossia, abbiamo che
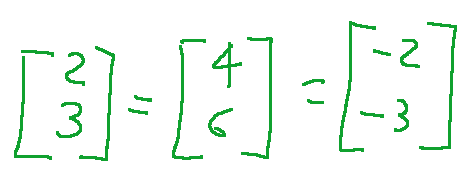
Definizione di spazio proiettivo
Uno spazio proiettivo
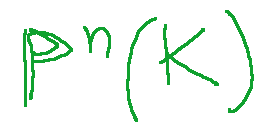
definito su un campo K è l’insieme delle rette passanti per l’origine nello spazio vettoriale
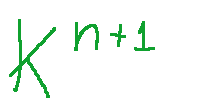
Ogni punto dello spazio proiettivo corrisponde a una direzione nello spazio vettoriale
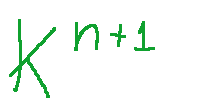
Formalmente abbiamo la seguente scrittura
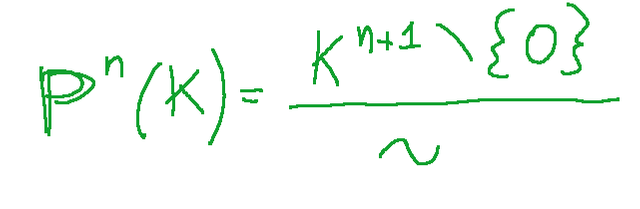
Conclusioni
Gli spazi proiettivi rappresentano una naturale estensione degli spazi affini che consente di studiare la geometria in modo più completo e generale. Introdotti per risolvere problematiche come il parallelismo e per unificare il trattamento dei punti "all'infinito", questi spazi offrono una struttura matematica ricca e potente.
Domanda
Avete mai studiato a scuola gli spazi proiettivi?
THE END
This post has been upvoted by @italygame witness curation trail
If you like our work and want to support us, please consider to approve our witness
Come and visit Italy Community
Hi @stefano.massari,
my name is @ilnegro and I voted your post using steem-fanbase.com.
Come and visit Italy Community