COMENZANDO 1ER TEMA FACTORIZACIÓN
Para entrar en el mundo de la matemática universitaria es importante conocer ciertos temas básicos que nos ayudarán a desarrollar todo tipo de ejercicios desde lo mas sencillos hasta los mas complicados a lo largo de este tutorial en matemáticas podremos aprender todo lo referente a ello COMENZAMOS.
FACTORIZACIÓN POR FACTOR COMÚN
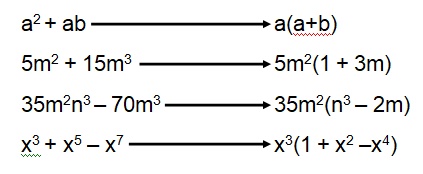
Un polinomio posee factor común, cuando en todos sus términos se encuentra el mismo factor. La factorización es igual al factor común que multiplica a la suma algebraica de los cocientes de cada término entre el factor común.
Ejemplos:
FACTORIZACION POR AGRUPACIÓN DE TÉRMINOS
En este tipo de factorización, se saca un factor común a la mitad de los términos y otro factor común a la otra mitad, procurando que los dos paréntesis sean iguales, para finalmente sacar como factor común el paréntesis.
Ejemplos:
- xa + xb + ya + yb
xa + xb + ya + yb = xa + xb + ya + yb
- mx + my - ya + yb
Sacamos como factor común m; m(x + y) + (x + y) y finalmente (x + y); así: (x + y)(m + 1).
mx + my - ya + yb = (x + y)(m + 1)
FACTORIZACIÓN POR CUADRADO PERFECTO
Un trinomio es cuadrado perfecto cuando dos de sus términos son raíces exactas y el tercero es igual al producto de dichas raíces. La factorización es igual a la suma algebraica de las raíces elevadas al cuadrado.
Ejemplos:
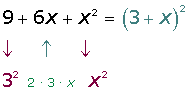
FACTORIZACIÓN POR DIFERENCIA DE CUADRADOS
Una diferencia de cuadrados es igual a la suma por la diferencia de sus raíces.
Ejemplos:
FACTORIZACIÓN del trinomio de la forma
Para que este trinomio sea factorizale es necesario que el segundo término sea igual a la suma algebraica de dos números, y el tercer término igual al producto de dichos números.
Ejemplo:
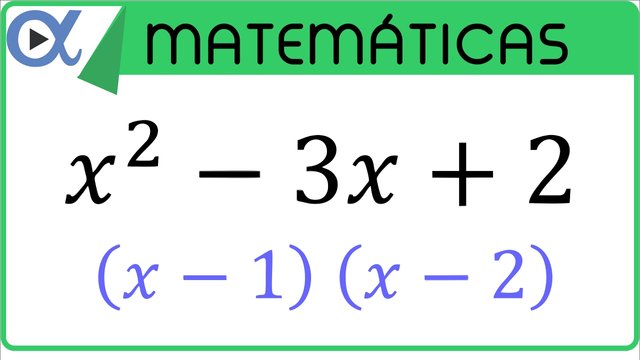
Una manera sencilla de resolver es buscar dos números que multiplicados me den 2 y sumados me den 3 por lo que el resultados sería (x - 1)(x - 2).
Otro ejemplo tenemos:
FACTORIZACIÓN DE SUMAS O DIFERENCIAS DE CUBOS
Se aplican las siguientes identidades para esta factorización:

Ejemplos:
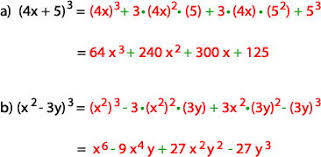
FACTORIZACIÓN POR RUFFINI
Aplicando Ruffini podemos calcular las raíces enteras de una ecuación de grado superior al segundo, para lo cual procedemos así:
- Descomponemos el término independiente de la ecuación en sus divisores.
- Aplicamos Ruffini tanteando con dichos divisores, hasta que el residuo de 0.
- El número de raíces de la ecuación es igual al mayor exponente de la incógnita.
Ejemplos:
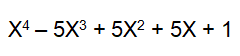
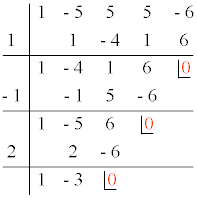
Dando como resultado: X1=1 , X2=-1 , X3=2
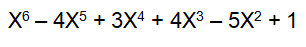

Dando como resultado: X1=1 , X2=1 , X3=1 , X4=-1
Observaciones:
Al tantear con los divisores del término independiente, se consideran como positivos o como negativos, según convenga.
No importa en qué orden se tomen los divisores.
Cuando el polinomio no está completo, al aplicar Ruffini, los términos que falten se completan con ceros.
Cuando el cociente sea una ecuación de segundo grado, se puede resolver aparte con la formula de segundo grado.
Esto será todo por hoy nos vemos en una próxima publicación donde veremos como aplicar todos lo métodos de factorización nombrados hoy HASTA LA PRÓXIMA.
- Descomponemos el término independiente de la ecuación en sus divisores.
- Aplicamos Ruffini tanteando con dichos divisores, hasta que el residuo de 0.
- El número de raíces de la ecuación es igual al mayor exponente de la incógnita.
Ejemplos:

Dando como resultado: X1=1 , X2=-1 , X3=2

Dando como resultado: X1=1 , X2=1 , X3=1 , X4=-1
Observaciones:
Al tantear con los divisores del término independiente, se consideran como positivos o como negativos, según convenga.
No importa en qué orden se tomen los divisores.
Cuando el polinomio no está completo, al aplicar Ruffini, los términos que falten se completan con ceros.
Cuando el cociente sea una ecuación de segundo grado, se puede resolver aparte con la formula de segundo grado.
Esto será todo por hoy nos vemos en una próxima publicación donde veremos como aplicar todos lo métodos de factorización nombrados hoy HASTA LA PRÓXIMA.
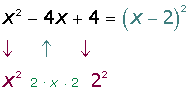
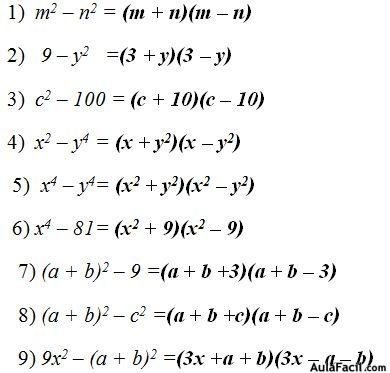
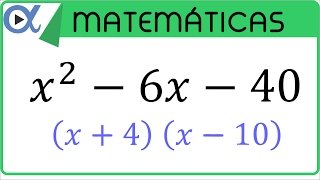
Mucho potencial en tu artículo te recomiendo colocar referencias
Congratulations @caosjesus! You received a personal award!
Click here to view your Board
Congratulations @caosjesus! You received a personal award!
You can view your badges on your Steem Board and compare to others on the Steem Ranking
Vote for @Steemitboard as a witness to get one more award and increased upvotes!