The flight of the bumblebee - Il volo del bombo [EN] / [ITA]

There is a common myth about bumblebees’ capability to fly, often claimed as an argument to stress the limits of science. It can be found in various forms and in various places (even on the internet) but generally it affirms that bumblebees should not be able to fly because their structure is too bold and their wings too tiny, so it is aerodynamically impossible for them to achieve flight. It is commonly known that bumblebees (Bombus terrestris) actually can fly but the real challenge is to explain how this is perfectly possible. First of all, we can easily affirm that the common mistake done by the supporters of this wrong myth is to consider only the shape of the bumblebee and trying to explain its flying in a similar manner to the one used for fixed wing aircraft. Being a long time aerodynamics teacher, I will try to tell You something about both ways of flying (airplanes and bumblebees) in order to explain differences and similitudes in a comparative way. It will not be so hard but a little knowledge is required so I will start from the very basic flight principles and then I will guide the reader through the wonderful world of fluid mechanics. It will also not be a quantitative calculation about aerodynamic forces but a qualitative description of the physics involved. I will try to explain this using the right arguments but I will also try to keep the things easy fore those who are not so familiar with the principles of flying.	Esiste una leggenda metropolitana sul volo dei bombi (anche se spesso in Italia vengono confusi con i calabroni che però sono anatomicamente molto diversi) spesso citata da qualche mal informato come argomento per esporre al pubblico i limiti della scienza: si può trovare ormai ovunque e spesso anche su internet. Semplicemente si afferma che il bombo non potrebbe volare a causa del suo corpo troppo tozzo e delle ali troppo piccole e per questo il fatto stesso che voli sfugge alle leggi conosciute dell'aerodinamica (il bombo - Bombus terrestris - è effettivamente un insetto che visto con superficialità potrebbe apparire piuttosto sproporzionato anche se, come vedremo in seguito, la Natura non ha sbagliato nulla nei suoi riguardi). Lo stesso fatto che il bombo sia in grado di volare è la migliore testimonianza che il suo volo sia possibile ma la vera sfida è spiegarne il perchè. Prima di tutto, l'errore comune è di considerare il volo del bombo, che ha una forma un po' insolita, esattamente con le stesse metodologie che si applicherebbero al funzionamento di un aeroplano qualsiasi. Da vecchio insegnante di aerodinamica cercherò di spiegare comparativamente entrambe le metodologie di volo (aerei e bombi) per identificarne similitudini e differenze. Non è difficile ma per farlo occorre la conoscenza di alcuni concetti di base che spiegherò all'inizio, guidando poi il lettore nel fantastico mondo della fluidodinamica. Non sarà uno studio quantitativo sul calcolo delle forze aerodinamiche ma piuttosto qualitativo, impostato sulla comprensione dei principi: cercherò di condurlo in modo rigoroso ma allo stesso tempo accessibile a chiunque.
Air and its components	L'aria e i suoi componenti
Let’s talk about air: we all breath this complex gas mixture formed primarily by nitrogen (N2) and oxygen (O2) molecules. For our scopes we can simple consider a mixture composed by N2 at 80% and O2 at 20%, disregarding the presence of other elements like vapors of water (H2O) and so on. Since we have this great variety of molecules in the air, we have to define the concept of air particle: this is a very little three-dimensional region of space containing a very great number of gas molecules. I often joke in my classes about how many molecules we can found in a particle and I say that we must consider at least 80 molecules of nitrogen and 20 of oxygen. Since the mean distance between molecules in a gas varies in accordance to its pressure and temperature, it is impossible to know the exact volume of this particle but I assure this is extremely small because a single molecule of oxygen has a covalent radius of 0.66 Å and the covalent radius of a single molecule of nitrogen is 0.71 Å. An angstrom [Å] is the equivalent of 10-10 m and it is the commonly unit used when dealing with atoms and molecules. It is exactly 0.000001 mm.	Parliamo dell'aria. Tutti respiriamo questa miscela composta di gas formata principalmente da molecole di azoto N2 ed ossigeno O2. Per i nostri scopi possiamo semplicemente accontentarci di una composizione pari all' 80% di N2 ed il 20% di O2 trascurando la presenza di altre molecole come il vapore acqueo H2O e l'anidride carbonica CO2. Dal momento che abbiamo a che fare con questa grande quantità di molecole cerchiamo di definire il concetto di particella: essa è una regione tridimensionale di spazio arbitrariamente piccola che però contiene al suo interno un numero molto grande di molecole. Scherzosamente dico ai miei studenti che per fare una particella servono almeno 20 molecole di ossigeno e 80 di azoto. La distanza media tra molecole in un gas dipende principalmente da pressione e temperatura quindi nessuno conosce esattamente le sue dimensioni anche se siamo sicuri che sia estremamente piccola in quanto una singola molecola di ossigeno ha un raggio covalente di 0.66 Å mentre quella di azoto 0.71 Å. Un angstrom [Å] è l'equivalente di 10-10 m ed è l'unità di misura comunemente usata quando si ha a che fare con atomi e molecole. Equivale esattamente a 0.000001 mm: unità molto piccole ma utilizzate nel micromondo.

Particles	Particelle
In the image above some bright dots represent the air particles at rest in a two-dimensions region of space. Even if very low, each particle has its own mass. In a square cube of air at 15°C at sea level, we have enough particles to produce a global mass of 1.225 kg. We can introduce the concept of air density (mass divided by volume) defining its standard value as 1.225 kg/m3. Another important fact that can be easily understood is friction: there is friction even between contacting particles, like between every other couple of contacting objects. This friction, as Ludwig Prandtl, a German Physicist, demonstrated in the ‘30s, is the main responsible of drag (the resistance of the fluid to the motion of objects) but we need to look deeper in its meaning in order to understand some phenomena. Let’s start a crazy conceptual experiment: just imagine to milk a cow in order to obtain a liter of milk. It will weight something around 1 kg. If You stir the milk with a spoon, You can feel some opposing friction forces. Now take that milk and, adding some very light (almost weightless) cocoa powder, prepare a hot chocolate in the right way . At the end, if You try to stir the chocolate, the opposite forces should be much more intense (if not, You absolutely have to change Your receipt). Note that the density of the fluid is almost the same as before (roughly 1 kg/dm3) but what is changed - the friction between particles - is called viscosity. Viscosity can be measured in the simplest way for liquids using a viscosimeter, a funnel in which the fluid can be poured: more time the fluid takes to pass through the funnel, greater is its viscosity. All fluids have some viscosity, even if it is very low (this is the case of the air). There is a simple challenge at this point: understanding how much viscosity influences the fluid motion patterns. The real strange thing is that if a particle of a viscous fluid (and every real fluid is at some point viscous) is located on a solid surface, like a tube wall or a glass plate, it remains in the same place (it sticks on the surface) even if the other particles not contacting that surface are moving: note how a drizzle droplet on the windshield of a car barely moves even speeding up: the air particles sticking on the windshield keeps the droplet there: wipers should not be required only in a zero viscosity environment! In the next picture we will see the effect of viscosity on a streak of particles flowing left to right down a flat plate section. On the left the viscosity is low, on the right it is high. Note the pattern of the streak. The rounded geometry of it near the plate is due to differences of speeds between zero (the particle sticking on the surface the plate) and the others at the free-flow (the region of the stream not interested by the plate) speed.	Nell'immagine sopra i puntini chiari rappresentano le particelle stazionarie in una regione di spazio bidimensionale. Anche se è molto bassa, ogni particella è dotata di una certa massa: in un metro cubo di aria a 15° C al livello del mare troviamo abbastanza particelle da produrre una massa globale di 1.225 kg. Introduciamo il concetto di densità (massa divisa per il volume o massa volumica) che in questo caso standard corrisponde proprio a 1.225 kg/m3. Altro argomento importante ma facile da capire è l'attrito: esso si esercita anche per contatto tra particelle come per qualsiasi altri corpi. Questo attrito, come ha dimostrato negli anni '30 Ludwig Prandtl, un fisico tedesco, è il principale responsabile della resistenza aerodinamica al moto degli oggetti ma occorre approfondire l'argomento per capire meglio alcuni fenomeni. Mettiamo in atto un curioso esperimento concettuale: immaginate di mungere un litro di latte da una mucca. Avrà una massa di circa 1 kg. A questo latte aggiungete un po' di polvere di cacao che ha massa praticamente trascurabile e preparate nella giusta maniera una cioccolata calda. Alla fine, se provate a mescolare con un cucchiaino la cioccolata calda sentirete una maggiore resistenza da parte del fluido rispetto al caso in cui vogliate mescolare solo il latte (se non fosse così dovete assolutamente cambiare la vostra ricetta per la cioccolata calda). Va notato che la densità dei fluidi è praticamente la stessa (circa 1 kg/dm3 ma quello che è cambiato è l'attrito tra le particelle, ovvero la viscosità. La viscosità dei liquidi può essere misurata con un semplice viscosimetro ovvero un imbuto nel quale si rovescia il liquido cronometrandone il tempo di attraversamento: maggiore sarà e più grande risulterà la viscosità del liquido. Tutti i fluidi hanno una certa viscosità, anche se piccola come per l'aria. La sfida sta nel capire come la viscosità influenzi il moto delle particelle fluide. La cosa davvero strana è che se la particella di un fluido viscoso (tutti i fluidi lo sono) è a contatto con una superficie solida come una parete di tubazione o una lamina di vetro, essa rimane appiccicata nella stessa posizione rispetto al solido anche se le particelle non direttamente a contatto con lo stesso si muovono. Notate come le gocce di pioviggine rimangono attaccate al parabrezza di un'auto anche aumentando la velocità: le particelle attaccate al vetro tengono le goccioline ferme anche se le particelle non a contatto con il vetro si stanno muovendo. I tergicristalli non sarebbero stati inventati in un mondo senza viscosità! Nell' immagine sotto vedremo gli effetti della viscosità su una lamina piana investita da un flusso (raffigurando uno "strato" verticale di particelle) che viaggia orizzontalmente verso destra. Nell'immagine a sinistra la viscosità è bassa, i a destra è alta. Notate la forma dello strato. La zona arrotondata è dovuta alla variazione di velocità tra zero ( le particelle a contatto con la lamina) e quella delle particelle circostanti.
Viscosity alone is not enough to understand the motion of the fluid over an object: heuristically it is easy to understand how for a very small object the friction between particles is much more relevant than for a bigger body. We will stress this later. It is basically a scale problem. I represented the same experimental condition for a much shorter plate in the same images. Same speed, same low viscosity (left), same high viscosity (right).	La viscosità da sola non è sufficiente per comprendere il movimento di un fluido attorno a un corpo: euristicamente è facile capire come un oggetto molto piccolo sia più assoggettato all'attrito fra particelle rispetto a quanto possa accadere per un oggetto molto più grande. Approfondiremo l'argomento in seguito ma è principalmente un problema di scala. Ho rappresentato le identiche condizioni (bassa viscosità a sinistra, alta a destra) per una lamina più corta nelle prossime immagini.
Note that the region of fluid interested by friction forces for the small plate has a dimension similar to the one of the object inserted in the flow. The big object is -proportionally- less interested by this phenomena. This is of great importance because we now have to deal with scaling parameters. Generalizing, a big object is less affected by viscous phenomena than a smaller one. Scaling down to the size of a particle (whatever it will be) makes this situation more and more relevant. This is the first important conclusion: the aerodynamics of a tiger should be different from the one of a cat simply because, even if their shape is similar, they differ in size. They actually move at similar speeds but this is another history since both should not be able to fly. Note that for smaller sizes even the surface condition (rough or smooth) is important but we are not talking about golf balls, at least not now. The main scaling parameter is called the Reynolds number (Re). It is defined by the formula:	Notate come la regione del fluido interessata dalle forze di attrito abbia dimensioni similari a quelle dell'oggetto immerso nel flusso. L'oggetto più grande visto prima è -proporzionalmente- meno interessato da questo fenomeno. Questo è molto importante in quanto abbiamo ora a che fare con dei parametri di scala. Generalizzando, un oggetto grande è meno interessato dalla viscosità rispetto ad uno piccolo. Rimpicciolirsi fino alla misura di una particella (qualunque essa sia) rende questa situazione sempre più rilevante. Qui la prima importante conclusione: l'aerodinamica di una tigre è diversa da quella di un gatto perchè, anche se la loro forma è simile, hanno dimensioni diverse. Tra l'altro si muovono alla stessa velocità ma qui la questione è diversa in quanto entrambi non volano. Va detto anche che per dimensioni piccole le condizioni della superficie (liscia o corrugata) cominciano ad incidere ma non stiamo parlando (almeno non per ora) delle palline da golf. Il parametro di scala più importante è conosciuto come numero di Reynolds (Re) che è definito dalla seguente formula:
Re=(rho V l )/Mu	Re=(rho V l)/ Mu
Where rhois air density, V the flow speed, l the characterizing length the object (from the nose to the tail for aircraft) and Mu is viscosity (Mu - did You remember the cow? Moooow!). Since we have V and l at the numerator it is easily understandable how big and fast objects have a grater Reynolds number than smaller and slower ones. Air parameters like density and viscosity are not something we can modify because they vary basically only with altitude or temperature.	Dove rho è la densità dell'aria, V la velocità del flusso indisturbato, l la lunghezza caratteristica e Mu la viscosità. Ricordate di aver fatto l'esperimento con la mucca vero? Siccome V ed l sono al numeratore è facilmente comprensibile come oggetti grandi e veloci abbiano numeri di Reynolds grandi rispetto ad oggetti piccoli e lenti. Gli altri parametri dell'aria come densità e viscosità non sono qualcosa che si possa variare a piacere in quanto dipendono essenzialmente da altezza o termperatura.
Differences	Differenze
A fast and big object in a low viscosity fluid (like real aircraft in the air) may have the same Reynolds number of a smaller and slower one in a high viscosity fluid (like a model aircraft in a water filled hydrodynamic facility) and they basically are affected by the same fluids dynamics phenomena. Below it is represented the same object (a stationary cylinder-like section) in a low viscosity fluid (left) and in a high viscosity fluid (right). As you can see, the fluid behaves very differently!	Un oggetto grande e veloce in un fluido a bassa viscosità (come un vero aeromobile nell'aria) potrebbe avere lo stesso numero di Reynolds di un oggetto più piccolo e più lento in un fluido a viscosità maggiore (come un modellino in una vasca idrodinamica riempita con acqua) e sono entrambi influenzati dagli stessi fenomeni fluidodinamici. Qui sotto è rappresentato lo stesso oggetto (una sezione statica di un cilindro) in un flusso a bassa viscosità (a sinistra) e in uno ad alta viscosità (a destra): Si noti come il fluido si comporta in maniera moto differente!
Since the Reynolds number varies also with length, let’s say it should be near zero on the nose of a conventional aircraft and rises linearly up to many millions in the tail region. Now You are ready to know that a typical Reynolds number for an airplane at 100 mph can increase, in standard conditions, roughly about 1,000,000 for each foot of length. In a 5 meters (15 feet) wing chord line airfoil at 100 mph, Reynold number is about 15,000,000 (chord is the segment between wing leading edge and wing trailing edge - check the illustration in the next part of the article). It can be noted that for a Bumblebee, which doesn’t fly at 100 mph but flaps its tiny wings very fast, let’s assume at the same speed of 100 mph even if it is a quite great value, if its wing chord is, let’s say, 5 mm, its Reynolds number should not be greater than 15000, 1000 times smaller than the previous one.	Dal momento che il numero di Reynolds varia anche con la lunghezza, possiamo dire che sarà zero sul muso di un aeromobile convenzionale per aumentare linearmente fino a vari milioni nella regione di coda. Siete pronti a sapere che un tipico numero di Reynolds per un aereo a 100 mph (160 km/h) può aumentare, in condizioni standard, di circa un milione per ogni 30 cm di lunghezza. In un'ala di corda pari a 5 metri a 160 km/h il numero di Reynolds sarà di circa 15 milioni (la corda (chord) è il segmento tra i bordi di entrata e di uscita di un profilo alare ed è rappresentata in una immagine successiva). Si noti che per un bombo non vola a 160 km/h ma sbatte le alucce molto velocemente. Assumiamo che riesca a "flappeggiare" le alette a 160 km/h anche se è un valore molto alto e che abbia un'ala di soli 5 mm di corda: il suo numero di Reynolds sarà di circa 15000, mille volte più piccolo di quello dell'aereo.
Numerical notes	Considerazioni numeriche
Numerical Note: the diameter of a N2 molecule is 0.00000142 mm and the one of O2 is 0.00000132 mm: being N2 the main component of air (80%), we can assume a mean molecular diameter of 0.0000014 mm for each molecule. It is 3,571,428 times smaller than the bumblebee chord or about 3,571,428,571 smaller than the jetliner. The Bumblebee is 1000 times smaller than the jetliner and its Reynolds number is 1000 times smaller also at the same speed: this is not surprising if You double check the formulas I have written above. If we want to know the Reynolds number for the aft fuselage of the airliner, let’s say for a 20 meters long jetliner at a speed of 250 knots (125 meters per second), it will counts something around 165,500,000 but the one of a 20 mm bumblebee flying at 3 meters per second is “only” 4000: 41,375 times lower! We can so think at the Reynolds number like a sort of dimensional ratio between the object in the flow and the particles of the fluid. Simplifying: when we have to deal with a very small and very slow object, fluid molecules or particles “appear” big if related to it. I often ask my students to imagine to be in a plastic bubble pool like the ones where often children play and then to imagine to try to “fly” like a little insect using the big particles represented by bubbles while flapping the arms. This is a funny simulation that is almost valid for every low Reynolds number environment like insect’s flying scenarios.	Il diametro di una molecola di N2 è di 0.00000142 mm mentre per l' O2 è di 0.00000132 mm: essendo l'azoto (N2 ) il principale componente dell'aria potremmo assumere un diametro molecolare medio di 0.0000014 mm. Questo è 3,751,428 più piccolo della corda dell'ala del bombo e 3,571,428,571 rispetto all'aereo. Il bombo è 1000 volte più piccolo dell'aereo e il suo numero di Reynolds 1000 volte più basso se misurato alla stessa velocità. Questo non è sorprendente se si verificano le formule descritte sopra con attenzione. Se vogliamo calcolare il numero di Reynolds per la coda del jet che supponiamo lungo 20 m ad una velocità di 250 kts (450 km/h) scopriremo che sarà circa 165,5000,000 ma per un bombo di 3 cm a 3 metri al secondo (10.8 km/h) varrà circa 4000: 41,375 volte più basso!. Possiamo anche pensare al numero di Reynolds come ad un rapporto dimensionale tra oggetto immerso nel flusso e diametro delle particelle dello stesso. Semplificando: se ci rimpiccioliamo molto le particelle d'aria ci sembreranno in qualche modo più grandi. Spesso chiedo ai miei studenti di immaginarsi a nuotare in una di quelle piscine con le palline di plastica in cui spesso giocano i bambini e quindi di provare a "volare" sbattendo le braccia a mo' di ali. Questa è una curiosa ed esagerata simulazione di come possano apparire "grandi" le particelle d'aria agli insetti molto piccoli ma è valida anche per capire come si possano comportare le particelle di un fluido a basso numero di Reynolds, anche se in realtà è una similitudine un po' sproporzionata.
Flying like an airplane	Volare come un aereo
The simplest way to fly is the one of the airplane. Wings are shaped to push the air downward and, as per Newton’s third law of dynamics, an upward reaction is achieved. The section of the wing, called airfoil, is shaped in a way that is the result of decades of research. It can be different if we compare different types of airplanes but basically it does the same job. Note in the next picture the streamlines that go left to right and how the angle between them and the airfoil’s chord influences the global pattern of the flow. On the right side I will also add the basic terminology we just used.	Il metodo più semplice di volare è quello degli aeroplani. L'ala ha una forma tale da riuscire a spingere dell'aria verso il basso, ottenendo così una reazione verso l'alto grazie al terzo principio della dinamica. La sezione dell'ala, chiamata profilo, ha assunto la forma odierna grazie a decenni di ricerca. Può differire da aereo ad aereo ma di fatto compie lo stesso lavoro su ogni modello. Da notare nella prossima immagine le linee di corrente, che corrono da sinistra verso destra e come l'angolo tra le stesse ed il profilo influenzi il flusso. Sulla destra ho anche riportato la terminologia. Per l'italiano: chord=corda e angle of attack=incidenza.
Unfortunately if this angle (called angle of attack) reaches a value that is too big, the flow will be separated in two distinct flows: this condition is known as stall.	Sfortunatamente se l'angolo di incidenza raggiunge valori eccessivi il flusso verrà separato in due parti: questa condizione è conosciuta come stallo.

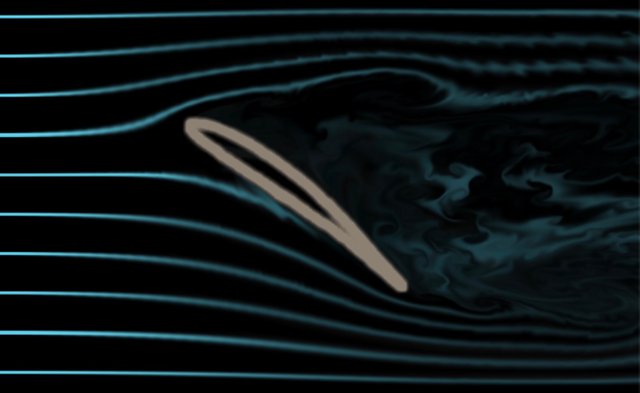
Pressure

Pressione

As a result of this turning of flow, we can easily guess how a greater distance between the particles on the upper side is the responsible for a decrease of static pressure. This is a situation very similar to the one You can achieve bending something like a plastic pen: on the outer side of the curved (bent) objects its particles (whatever them will be) are more distant each from another and in the lower side them will be somehow compressed. Stressing the bend can also result in a cracking that is not like a stall but it helps to remember that this “turning” is in some ways limited. This “bending” phenomena in a fluid like air is the main responsible of pressure variation around an airfoil. In the picture below the pressure (when it is low the color is blue). Check also the augmented distances between the upper particle’s streaks.

Il risultato di questa rotazione del flusso può far facilmente considerare come ci sia maggior distanza tra le particelle che percorrono la parte superiore del profilo e come questo sia responsabile di un abbassamento della pressione statica: questa situazione è simile a quella che si ottiene piegando un oggetto in plastica come una penna. Nel lato esterno rispetto alla curvatura le particelle della plastica saranno tese (più distanti) rispetto all'interno compresso (più vicine). Esagerare la curvatura porterebbe anche alla rottura della penna (questo non c'entra nulla con lo stallo ma è bene ricordare che anche nell'aria la possibilità di ottenere variazioni direzionali è limitata). Comunque la curvatura stessa dell'aria è responsabile delle variazioni di pressione: nella seguente immagine notiamo come nella superiore la pressione sia inferiore (colore blu=bassa pressione) rispetto alla parte inferiore (colore rosso=alta pressione). Notare anche la distanza aumentata tra le particelle nella parte superiore rispetto a quella inferiore.

Forces	Forze
The force keeping the airplane in the sky, called lift, is the result of both phenomena (pushing air down and pressure difference). A common error is to consider only pressure difference: after some calculation it is possible to discover how this difference alone is not enough to lift the airplane.	La forza che tiene in volo l'aeroplano è chiamata Portanza ed è il risultato dei due fenomeni descritti: la spinta di aria verso il basso e la differenza pressoria. Un errore comune è considerare solo la differenza tra le pressioni: con semplici calcoli si noterà che ciò non sarebbe assolutamente sufficiente per sollevare il peso dell'aeroplano.
Let's talk about bumblebees	Torniamo ai bombi
Now it’s time to discover the secrets of the bumblebee’s flight. Since the thirties we know that trying to calculate the bumblebee’s lift in the way we use for airplanes does not work. The first one to note this was probably the French entomologist Antoine Magnan and it is likely that the “impossible flight of the bumblebee” myth was originated by these considerations.	E' ora di scoprire i segreti del volo del bombo. Dagli anni '30 sappiamo che se proviamo a calcolare la portanza del bombo utilizzando il metodo che useremmo per un aereo il risultato sarebbe insufficiente per permettere il volo. Il primo ad accorgersene fu probabilmente l'entomologo francese Antoine Magnan ed è possibile che il mito del volo impossibile per i bombi sia nato da queste considerazioni
Bumblebees are short winged if compared to an airplane. This basically is not a problem for their dimension as we will see in a moment. For now note that a bumblebee as big as an airplane will be supercool but it will not be able to fly, exactly like a very small airplane model scaled down to the size of the bumblebee.	I bombi hanno le ali piccole se paragonate a quelle di un aereo convenzionale. Questo non è certo un problema per le loro dimensioni come vedremo tra poco. Per adesso si noti che un aereo di linea a forma di bombo sarebbe bellissimo da vedere ma non volerebbe, esattamente come non volerebbe mai un insetto a forma di piccolo aereo.
Flapping its tiny winks many and many time per seconds, bumblebee is perfectly able to fly. Let’s say that it is possibile combining the phenomena already described with something we will discover now. Think at the wing of this insect: when it goes down (downstroke) it simply pushes the air down (and sometimes, angling the wing, also pushes the air behind or in front to develop horizontal motion and positional control). This surely create some lift, specially in this low Reynolds number environment (remember: if You are small You can see the particles bigger than if You are big). Sometimes the angle of attack is greater than the one of the stall condition but this works just because the air is pushed down anyway. Then the wing, in its lower flapping run, is rotated quickly to generate a vortex and moved a little forward. Even a vortex acts on the airflow like a wing does. In this simple experiment (see the video below) I put a clockwise turning fidget spinner near a candle’s flame. Note that the air particles, also turning clockwise because affected by the ones sticking on the spinner under the effects of viscosity) sucked the flame to the right in a similar way the airfoil does. In this case the flow was vertical and the lift component of the system was leftward but it can be easily understood how a vortex can deviate an airflow. It is the same effect, sometimes called Magnus effect, that we can see in sports: think at the baseball “curved ball”, at the horizontal trajectory of a spinning frisbee or at the draw and the fade (that are better than hooks and slices) in golf.	Sbattendo le sue piccole alucce molte volte per ogni secondo il bombo è perfettamente capace di volare. Diciamo che questo è possibile grazie ad una combinazione dei fenomeni già descritti con qualcosa di nuovo che scopriremo tra poco. Pensate all'ala degli insetti. Quando "rema" verso il basso semplicemente spinge in giù dell'aria (a volte, variando l'incidenza, anche un po' indietro o in avanti se necessitano traslazioni o correzioni posizionali): questo senza dubbio genera una certa portanza specialmente in condizioni di basso numero di Reynolds (ricordate che più siete piccoli e più grandi vi sembreranno le particelle d'aria). A volte l'angolo di incidenza è addirittura superiore a quello di stallo ma la cosa funziona ugualmente semplicemente perchè sta spingendo dell'aria verso il basso. A questo punto l'aletta, nel punto più basso della sua corsa, è velocemente ruotata e spostata in avanti in modo da generare un vortice. Anche il vortice agisce sull'aria come potrebbe agire un profilo alare: nell'esperimento riportato nel prossimo video ho posizionato un fidget spinner ruotante in senso orario vicino alla fiamma di una candela. Notate che le particelle d'aria attaccate allo spinner si trascineranno dietro molte altre particelle creando un vero e proprio vortice destrogiro e che di conseguenza devieranno la fiamma della candela verso destra in modo analogo a quello che farebbe un profilo alare. In questo caso il flusso è verticale dal basso verso l'alto (la candela) e la componente di portanza sarebbe diretta a sinistra in quanto il flusso viene deviato verso destra ma è comunque facilmente comprensibile immaginare cosa avverrebbe quando un flusso orizzontale incontra un vortice. E' lo stesso effetto, chiamato appunto effetto Magnus che notiamo negli sport, come ad esempio nel "tiro ad effetto" dei giocatori di football, il "topspin" delle palline da tennis o i numerosi effetti possibili con le palline da golf o con i freesbee.

Even this vortex must be considered for lift calculations in this kind of insects, like the vortex that are eventually generated by the downstroke of the wing. Only recent technology permitted to discover the exact rotating motion at this point of the stroke.	Anche questo vortice va considerato per i calcoli della portanza su queste specie di insetti così come i vortici eventualmente generatesi dal movimento verso il basso con incidenza superiore allo stallo. Solo la recente tecnologia ha permesso di capire l'esatto movimento di rotazione dell'ala dei bombi in questa fase.
During the upstroke the wing is not so efficient because, to not push the air up and to not generate a downward reaction force, the intrinsic flexibility of its structure permits to do that with almost zero angle of attack in an almost vertically oriented fashion, almost like a blade in the upward movement egressing from an object after the cut.	Durante il movimento di ritorno verso l'alto l'ala non è così efficiente perchè, per non spingere aria verso l'alto creando una deportanza, la sua flessibilità intrinseca permette di risalire con un incidenza quasi nulla per via di un orientamento verticale un po' come farebbe la lama di un coltello che sale verso l'alto dopo aver tagliato qualcosa.
The wing is now at the top of the upstroke with an almost vertical chord. It is the moment when it is simply pushed forward, decreasing its angle of attack below the one of stall and acting almost like an airplane’s wing but as You have seen only in this last third of the action.	L'ala è ora nel punto più alto del suo movimento con una corda quasi verticale. Questo è il momento ove è semplicemente spinta in avanti, riducendo il suo angolo di incidenza al di sotto di quello di stallo e funzionando finalmente come una normale ala di aereo ma solo per questo ultimo terzo di azione.
Let's try to imagine a bumblebee flying to the left as the one depicted in the next photo: in the animation below You can find the motion of the wing	Immaginiamo ora un bombo volare verso sinistra come quello ritratto nella foto: nella successiva animazione sarà visibile il movimento dell'ala

In this final animated gif I tried to simplify the motion of the wing. The bumblebee is flying to the left (if You prefer, its head is on the left). The only part that it is not presented here is the passive upstroke when it acts like a knife. I described the active phases of the action only. Note that the bumblebee’s wing is not airfoil shaped but I created this image to show exactly the leading (forward) and the trailing (rear) edges.

In questa animazione finale ho cercato di semplificare il movimento dell'ala. L'unica parte non rappresentata è la risalita passiva, quando l'ala si comporta come un coltello: ho inserito quindi solo le fasi attive del volo. Va anche notato che l'ala del bombo non ha questo tipo di profilo ma l'ho rappresentata così per distinguere il bordo d'entrata (anteriore) da quello di uscita (posteriore). La testa del bombo si troverebbe a sinistra e sta anche volando verso sinistra

The yellow arrows represents the motion, the white ones the vortex. You could note the greater intensity of the clockwise leading edge generated vortex (green areas) if compared with the trailing edge generated ones (red areas). So actually bumblebees can fly using three different ways: pushing the air downward (let’s call this brute force way) in the downstroke, creating some vortex (ehm… vortex way?) and turning streamlines downward (conventional way). At a higher Reynolds number (greater dimensions or faster speeds) this combination of factor is simply not efficient and it is why we will never see a spectacular bumblebee shaped big aircraft. I hope this can be, if not easy, at least fun to understand and I remain tuned in the comment section below for every consideration You want to share with us.

Le frecce gialle rappresentano il movimento, quelle bianche i vortici. Si può notare la maggiore intensità dei vortici orari generati dal bordo di entrata (colore verde) rispetto a quelli antiorari generati dal bordo di uscita (colore rosso). Possiamo affermare infine che il bombo utilizza tre differenti metodi per ottenere la condizione di volo: effetto di reazione dovuto alla spinta dell'aria verso il basso generata dalla battuta dell'ala (in un certo senso, forza bruta), effetto Magnus (vorticità) e solo alla fine la convenzionale (per gli aeroplani) interazione tra ala e vena fluida (incidenza). A numeri di Reynolds più grandi (dimensioni maggiori o velocità più elevate) questa combinazione di fattori sarebbe semplicemente inutile e questo è il motivo per cui purtroppo non vedremo mai spettacolari aerei a forma di bombo. Spero che tutto questo possa essere stato se non proprio facile almeno interessante e rimango disponibile nella sezione commenti per ogni considerazione vorrete condividere con noi.

---

SOURCES / FONTI:

• R. Dudley, C.P. Ellington, Mechanics of forward flight in bumblebees, Journal of Experimental Biology 148, 53-88 (1990)
• Wind tunnel simulations: wind tunnel app by Algorizk
• Animated gif: Makeagif
• Biographies: Wikipedia
• Photos: CC0 Pixabay
• Anatomy of insects: many posts of @phage93

---