확률론 or 실해석 (1): 두 가지 변수변환 정리
측도론을 공부하면 비슷하게 생긴 정리 둘을 마주칩니다.
첫 번째는 Rudin의 Real and Complex Analysis의 1장에 나오는 정리 1.29

두 번째는 Durrett의 Probability: Theory and Examples의 1장 6절에 나오는 정리 1.6.9

생긴 것도 비슷한데 증명도 똑같습니다. 그래서 더 헷갈렸던 것 같습니다.
- Characteristic Function(특성 함수)에 대해서 성립함을 보인다.
- Simple Function(단순함수)에 대해서 성립함을 보인다.
- Monotone Convergence Theorem을 써서 양함수에서 성립함을 보인다.
- 일반적인 함수에는 정의를 써서 잘 된다는 걸 보인다.
RCA의 첫 번째 정리는 동일한 공간 X위에 주어진 측도 μ와 φ의 관계를 기술하고 있습니다.
반면, Durrett는 서로 다른 공간 Ω와 S 위에 각각 주어진 측도 P와 μ사이의 관계를 기술하고 있습니다.
예시로 이 글을 마무리 하겠습니다.
Ω=R, X: 평균 = 0, 표준편차 = 1인 정규분포를 따라는 확률변수, S=R, f:R→R, f(x)=x라는 세팅을 생각해보도록 하죠. 그리고 Ω위의 측도를 P, S위의 측도를 φ, R위의 르벡측도를 μ로 표기합시다.
따라서 Ef(X)=EX이므로 단순히 기댓값을 구하는 문제입니다.
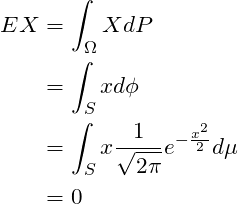
두 번째 줄에서 Durrett의 정리, 세 번째 줄에서는 RCA의 정리가 쓰였습니다. 적분이 일어나는 공간(인테그랄의 아래첨자)를 보시면 두 정리의 미묘한 차이가 뭔지 알 수 있을 것입니다.