문과 아재도 쉽게하는 R 데이터 분석 – (8) PCA(Principle Component Analysis)
Principal Component Analysis
안녕하세요. 오늘도 재미는 없지만 열심히 쓴 글을 풀러왔습니다. 어디서 따온글도 아니고 다 직접 쓴 글이구요, 좋아요를 받든말든 저는 제 갈길 갑니다 꺄하하하하
변수가 너무 많을때.
우리는 데이터 분석을 할때, 정말 많은 데이터 종류를 넣어서 예측을 합니다. 예를들어, 실제 물건이 얼마나 팔리는지 예측을 할때 이에 필요한 데이터는 광고데이터, 영업사원 데이터, 유행 데이터등 활용할만한 데이터들이 참 많습니다. 다만, 이러한 데이터들 하나하나가 차원으로 작동하게 되는데, 스캐터 차트등으로 확인하기가 힘듭니다.
그리고 설명변수들이 서로 상관이 더욱 높을때는 굳이 높은 차원으로 하나하나 구별해놓을 필요가 없습니다. 어차피 깔끔하게 공통적인 요인 하나만 분석하는것이 심플하고 예측력도 높아질것이기 때문이죠.
또한 초끈이론으로 13차원 분석을 할수가 없으니, 우리는 그냥 주요한 몇개의 특성만을 다시 추려내 데이터를 저차원 데이터로 변환해볼수 있습니다. PCA는 주요 컴포넌트 분석의 약자이며, 1차원부터 차례데로 현재의 데이터들을 잘 설명할수 있도록 지금 변수의 조합으로 다시 재조합합니다.
어떻게 줄이나?
일단 데이터 분산이 제일 많은 항목을 하나 뽑아내 이를 다시 한 축으로 둡니다. 분산이 크다는건, 해당하는 변수에 따라 데이터가 뭔가 잘 흩어진다는 뜻이므로, 제일 설명력이 높다고 볼수 있습니다. 이를 PC1로 두고 이에 수직인 축들을 PC2, PC3...로 나눕니다. PC는 차원수만큼 존재하게 됩니다.
항상 줄일수 있나?
만약 데이터들이 서로 상관이 없는경우, 모두 독립인 경우는 사실 PCA로 해서 차원을 줄여보았자 별 의미가 없습니다. 각자 다 나름대로의 이유를 가지고 있는데, 이를 차원을 확 줄이게 된다면 서로 잘 섞이지도 않을 뿐더러 그냥 변수하나의 설명력만 뭉텅 잘라내는 것밖에 되지 않습니다.
범죄 데이터로 살짝 맛보기
이번에의 데이터는 USArrests 데이터셋입니다. 이를 다음과 같은 코드로 간단하게 PCA를 돌려볼수 있습니다. USArrests데이터는 사실, 비슷한 종류의 변수들이 존재합니다. Murder, Assault, UrbanPop, Rape는 아무래도 상관관계가 높은 범죄종류일수밖에 없습니다.
p <- prcomp(USArrests, scale = TRUE)
이 결과를 바로 plot으로 찍어보면,
summary(p)
Importance of components%s:
PC1 PC2 PC3 PC4
Standard deviation 1.5749 0.9949 0.59713 0.41645
Proportion of Variance 0.6201 0.2474 0.08914 0.04336
Cumulative Proportion 0.6201 0.8675 0.95664 1.00000
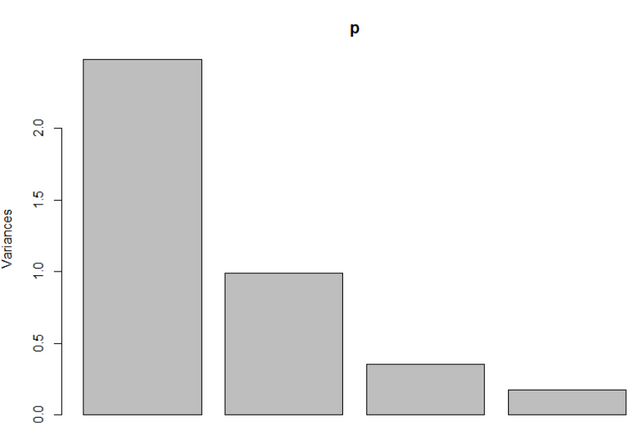
plot(p)
실제로 모든 USArrests의 변동이 한 첫번째 PC에 몰빵된것을 알수있습니다. 만약 모델을 짜려면,
y = ax1 + bx2 + cx3 + dx4 + e
같은 복잡한 식이 아닌
y = a * p + e
와같은 간단한식으로도 대부분 변수들의 움직임이 설명될수 있게 짤수 있을겁니다.
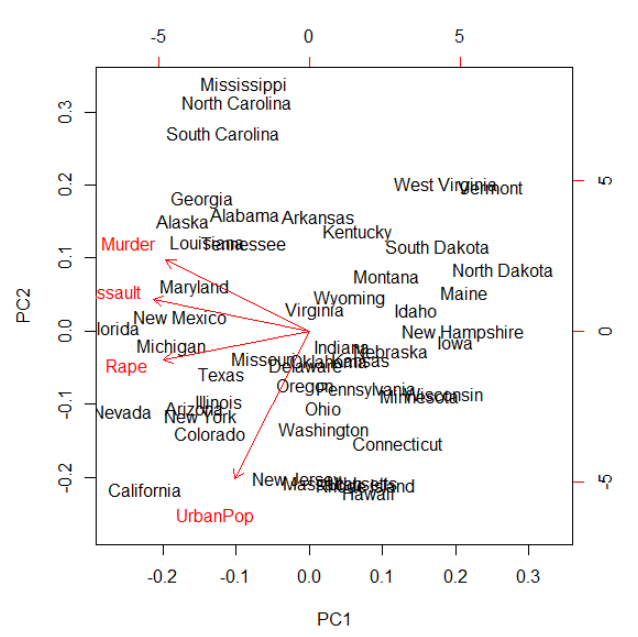
biplot(prcomp(USArrests, scale = TRUE))
위의 그래프를 통하면, 원래의 변수들이 어떤식으로 흩어져 있었는지도 확인할수 있습니다. 물론 차트는 제일 중요한 PC1과 그다음으로 중요한 PC2로 축들이 결정됩니다. 그이상의 우리 눈알에 보이지 않으니까요 ^.^
디시전트리로 이해하기
데이터를 주성분으로 표현하는 것은 결정 트리(decision tree)의 단계를 결정 단계를 밟아나가는 것과 유사합니다. 잘 만들어진 결정 트리는 첫번째 가지의 if-then-else가 가장 대표적인 질문이 되어야 하는데, 이것은 마치 PCA의 첫번째 주성분이 가장 엔트로피를 감소시키는 차원을 고르는 것과 같습니다.
분산이 낮아진다는것은 엔트로피가 감소하는것을 의미합니다. 데이터의 분포를 주성분으로 나타내면 성분의 차수가 낮아질수록 분산감소. 즉 하나로만 설명할수 있다는것입니다.
참조 및 시각화 사이트
밑의 사이트에서는 PCA를 쉽게 시각화해서 이해할 수 있습니다.
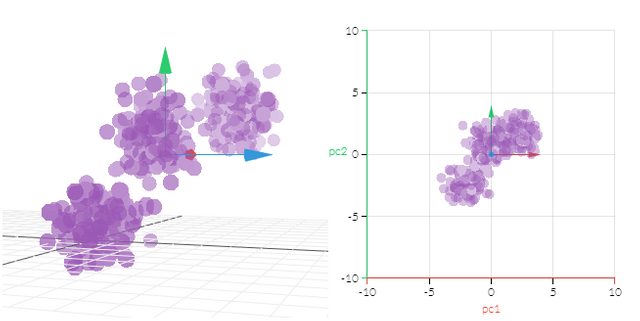
어렵네요. ㅎㅎㅎ
PCA는 아노말리 데이타에 직접 SVD를 적용하여 계산했었는데, 저렇게 펑션 하나로 딱 계산이 나오니 편하긴 정말 편하네요.
이론이 이해하기가 어려운데, 함수로 너무 손쉬워서 오히려 문제가 아닌가도 싶습니다 ㅋㅋ