백준 온라인 저지에서 문제를풀어보자 #4(2747번: 피보나치 수)
https://www.acmicpc.net/problem/2747
문제
피보나치 수는 0과 1로 시작한다. 0번째 피보나치 수는 0이고, 1번째 피보나치 수는 1이다. 그 다음 2번째 부터는 바로 앞 두 피보나치 수의 합이 된다.
이를 식으로 써보면 Fn = Fn-1 + Fn-2 (n>=2)가 된다.
n=17일때 까지 피보나치 수를 써보면 다음과 같다.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597
n이 주어졌을 때, n번째 피보나치 수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 n이 주어진다. n은 45보다 작거나 같은 자연수이다.
출력
첫째 줄에 n번째 피보나치 수를 출력한다.
풀이
이번문제는 피보나치 수열 문제입니다.
일단 기본적으로 생각해 볼 수 있는 방법은 가장 기본적인생각은 재귀함수 호출을 통한 방법이 있습니다.
실제로 학부생때 교수님 께서는 재귀함수에 관련된 부분을 강의해 주실때 피보나치수열을 구하는
메소드를 만드는 것으로 재귀함수에 대해 알려주셨었습니다.
재귀함수란?
자기가 자기를 부르는 함수 입니다.
예를들어 간단하게 구현해 본다면
이런식으로 tmp에 숫자 10을 담아서 주면 recursive함수 안에서 10에서 1을뺀값을
다시 recursive에 넣어서 n이 0일떄 리턴될때까지 돌아갈 수 있도록 만드는 방법입니다.
이 프로그램을 실제로 돌려보게 된다면
이런식으로 10에서 숫자를 하나씩 감소시키면서 돌아가는 모습을 볼수가 있습니다.
다시 돌아와서 피보나치 수열을 재귀함수로 구현하기위해서는
피보나치함수를 알아야 합니다.
피보나치 함수는
피보나치 수는 0과 1로 시작하며, 다음 피보나치 수는 바로 앞의 두 피보나치 수의 합이 된다.
라고 정의되어 있는데 이걸 수식으로 표현하게되면
f(n)=f(n-2)+f(n-1)로 나타낼 수 있습니다.
이 내용을 소스코드로 옮기게 된다면 이런 모양이 되는데요
n==0 일때는 0 n==1일때는 1 로 값을 돌려준다는 ==> 피보나치 수는 0과 1로 시작한다
fibo(n-1)+fibo(n-2); 이부분은 다음 피보나치 수는 바로 앞의 두 피보나치 수의 합이 된다. 라는 걸 구현해 놓은 부분입니다.
다만 해당소스에는 큰 문제가 있습니다. 바로 입력에서 n은 45개나 주어진다는 것인데요 이 값의 결과는
재귀를 통해 들어가 결국 0과 1을 더해서
1134903170
라는 큰수를 만들어야하는 구조입니다. 아주 비효율적이고
백준알고리즘에서 주어진
시간제한과 메모리제한을 통과할 수가......

얼라.. 통과하네요 흠흠...
무튼 좀더 빠른 프로그램을위해 계속 진행 하겠습니다.
재귀함수가 아닌 다른방법을 이용한다면 여기서 가장효율적인 방법은 다이나믹 프로그래밍
즉 DP 메모이제이션을 이용해 프로그램을 작성하는 것 입니다.
기존 재귀에서는 5번째 피보나치수인 3을 구하기위해서
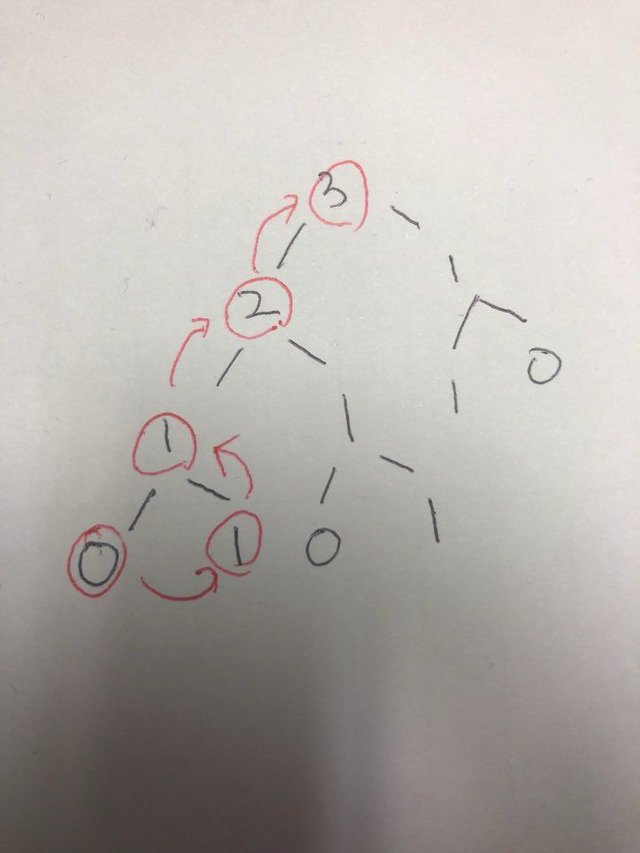
여기서 보이는 연산들을 전부 쌓아서 3이라는 숫자들을 만들게 됩니다.
매우 비효율 적이죠
그래서 이런 중복되는 연산을 피하기위해서 메모이제이션을 이용 할 수 있습니다.
원하는 피보나치수의 갯수만큼 배열을만들고
0번째 피보나치수인 0 은 0번째에 저장
1번쨰 피보나치수인 1 은 1번째에 저장
이런식으로 배열에 저장을 하면서 만들게되면 기존의 재귀함수보다 매우 빠른속도로
피보나치수열에 대한 연산을 할 수 있습니다.
결과적으로 작성한 소스코드는
이런식으로 작성 하시면 됩니다.
실제로 문제에 제출을 하게된다면 무려 60배가까이되는 큰 성능차이를 보여줍니다.
긴글 읽어주셔서 감사합니다. ㅎㅎ
문제를 많이 푸셨군요...
문제 풀기 번개라도 한번~~
ㅎㅎㅎ 스터디진행중이라 사실푼문제는 300문제가량됩니다 다만 쉬운것들만풀어서.....ㅎㅎ 번개치시면 꼭참석하겠습니닿ㅎ
@resteemator is a new bot casting votes for its followers. Follow @resteemator and vote this comment to increase your chance to be voted in the future!