[논문 소개] Size-constraint loss for weakly supervised CNN segmentation
- 논문 정보
- 논문 제목: Size-constraint loss for weakly supervised CNN segmentation
- 학회 정보: MIDL 2018 Conference Submission
- 논문 링크: https://openreview.net/forum?id=BkIBHb2sG
오늘 소개드릴 논문은 "Size-constraint loss for weakly supervised CNN segmentation" (https://openreview.net/forum?id=BkIBHb2sG) 입니다. MIDL에 제출된 논문입니다. MIDL은 Medical Imaging with Deep Learning의 약자입니다. 그냥 보시기에도 딱 의료 영상에 딥러닝 쓴 논문입니다.
이제 늘 그렇듯 제목을 보면, 3개의 주요 키워드로 구분됩니다. CNN segmentation.. CNN을 써서 segmentation하는 것이고, weakly supervised.. supervised 학습을 줄만한 상황이 아니라 annotation 정보가 어딘가 모지라보입니다. 이 두 단어는 어떤 문제를 풀건지에 관한 것이니, Size-constraint loss.. 이게 이 논문의 아이디어입니다. weakly supervised CNN segmentation에서 문제를 더 잘 풀기 위해서 segmentation 결과에 대한 size에 관한 constraint를 주는 loss를 추가하여 해결하겠다. 이 논문의 내용입니다.
그런데, 위 단어들 중 모호하게 정의된 것이 있다면, weakly supervised 입니다. 나머지는 하나는 지가 제안한거고, 하나는 CNN segmentation이라서.. 모호할게 없는데 이 놈은 좀 모호합니다. 실험 그림을 보면.. 아래와 같이 설명되어 있습니다.
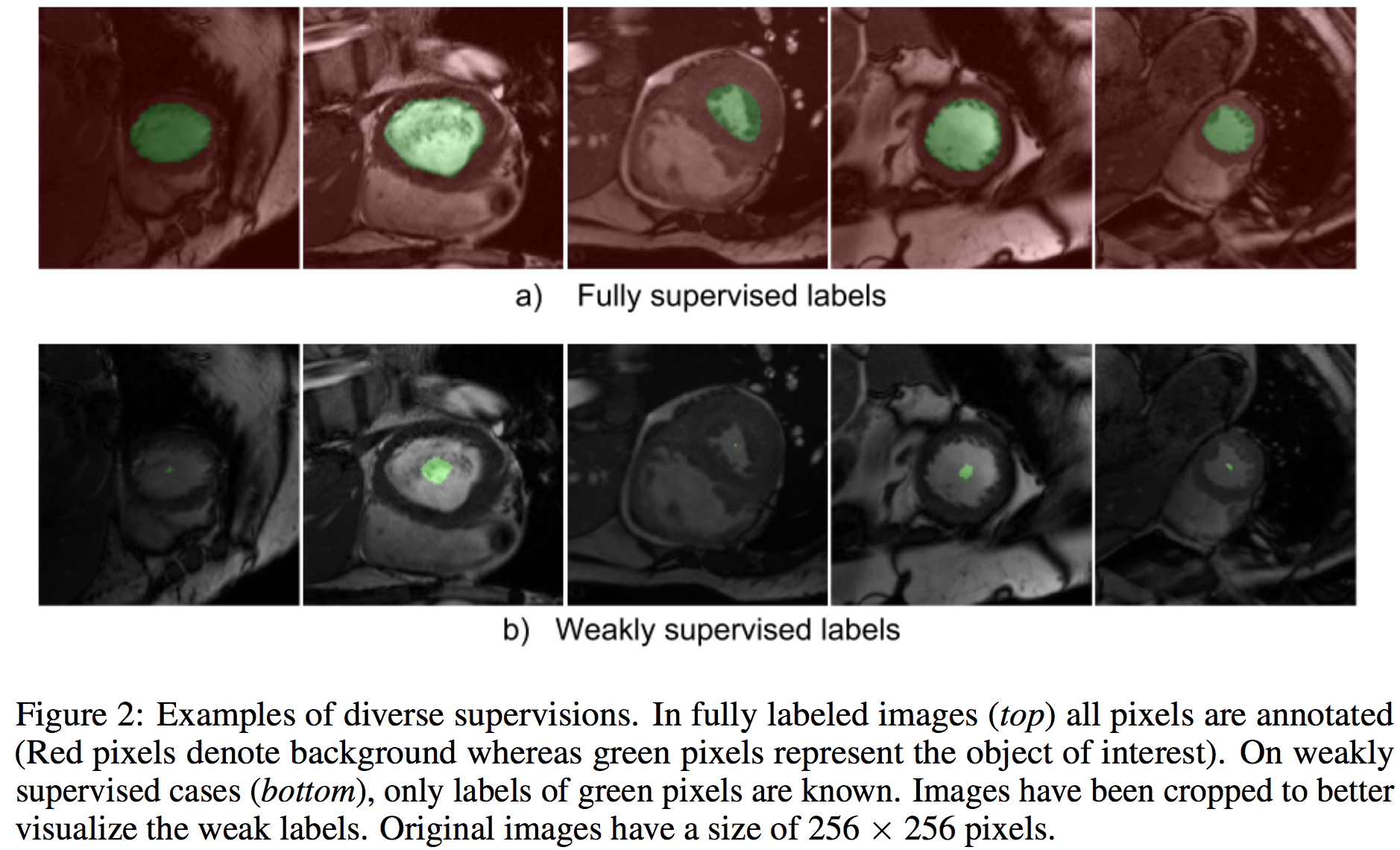
이 논문에서 주로 다루는 weakly label의 정의는 "a fraction of the ground-truth labels with image-level tags" 입니다. 그러니깐, 이 논문의 weakly는 기존 사람들이 사용하던 weakly.. 그러니깐 image-level tags의 정의와 partial 혹은 fraction된 label의 정의를 사용하고 있습니다. 그래서 위 그림처럼 실험을 위해서 기존의 제공된 ground-truth 영역을 모폴로지 필터같은 방식으로 작게 만들어 이게 weakly supervised라고 합니다.
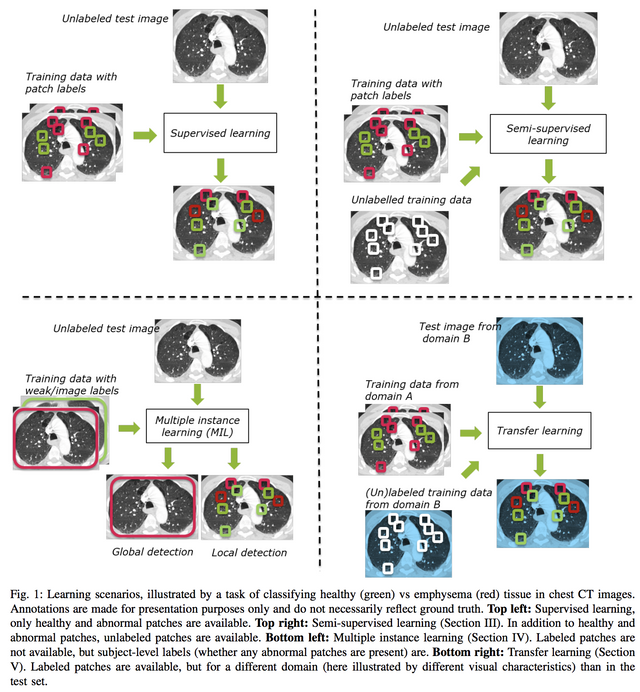
그럼 의료 영상에서 이런 개념이 헷갈리기 시작하실건데.. 언제는 semi고 언제는 partial이고 언제는 weakly냐.. 난 모르겠다.. 이러시면.. 최근 "Not-so-supervised: a survey of semi-supervised, multi-instance, and transfer learning in medical image analysis" (https://arxiv.org/pdf/1804.06353.pdf, 아직 어디에 투고전인 논문으로 읽다가 이상한거 있으면 저자에게 멜 보내야 하는 논문)을 보시면 아래 그림이 있습니다. 아래 그림에서 Multiple instance learning 부분을 보시면 아시겠지만 보통은 이미지 레벨에서의 뭔가 있다 없다의 정보만 있고 그 것의 local한 위치정보가 없을 시에는 weak라고 합니다. 그러니 이 논문의 weakly와는 약간의 차이가 있습니다.
다시 논문으로 돌아와서.. 돌다 와도 되는게 이 논문 단순하면서 재밋으니깐.. 기본적인 아이디어는 아래와 같습니다. 이렇게 segmentation에 대한 annotation이 fraction되었다고 보면, 일반적인 cross-entropy loss에 이 segmentation이 어느 정도의 크기여야 하는지 prior 정보를 그 segmentation의 size 구간 a,b로 주자 입니다.

그러니깐 a가 lower bound, b가 upper bound라고 보시면, 아래와 같이 범위를 벋어나면 혼나는 loss를 주자.. 입니다.

자 .. 이제 아이디어와 내용 설명 끝. 정말 단순합니다. 그런 범위의 구간이란 prior를 주는 것만으로도 fraction된 정보를 리커버하는데 도움을 줄 수 있다라는 내용입니다.

성능을 보시면, 상당히 효과가 있습니다. 그림으로 보면..
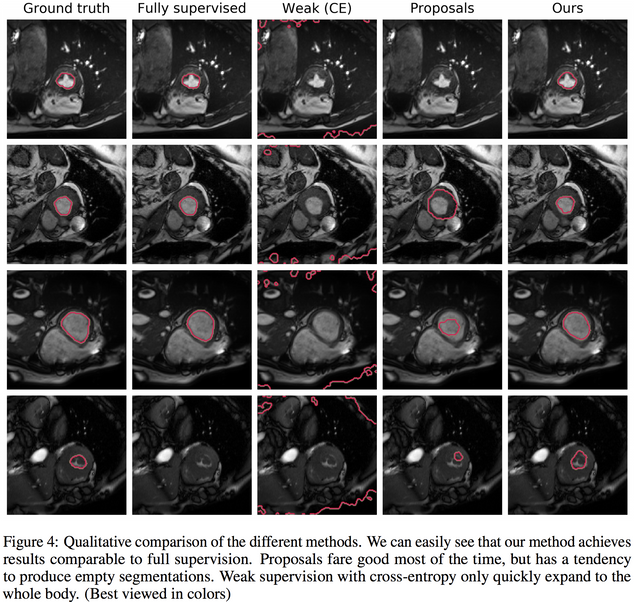
잘 됩니다. 해봐야지.. -_-
상당히 단순한 아이디어로 좋은 결과를 이끌어낸거 같습니다. 그닥 어려운 수식이 없어서 한번 바로 고민하던 문제에 적용이 가능한지 고민이 되네요. 오늘도 어렵지 않은 논문 리뷰 끝.