[수학] 제곱근의 근삿값 구하기 2 – 산술-기하평균

안녕하세요! ryanhan입니다.
저번 포스팅에서는 제곱근의 근삿값을 구하는 방법으로
‘바빌로니아 방법’이라고 불리우는 방법을 소개했습니다.
바빌로니아 방법은 루트2의 값을 구할 때,
루트2와 가까운 값(가까울수록 빠르게 구할 수 있어요~)
을 다음과 같은 점화식에 대입해서
루트2의 값을 구하는 방법이었습니다.
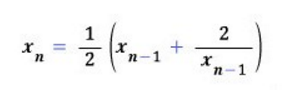
예를 들어, 루트2와 가까운 값으로 X0 = 1이라고 한다면,
X1 = 1.5
X2 = 1.417
두 번의 대입만에 참값과 매우 가까운 값을 구할 수 있었습니다.
오늘은 저 점화식이 나오게 된 이유를 생각해보겠습니다.
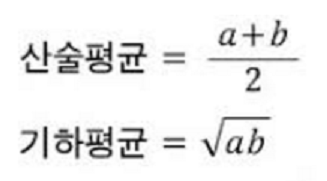
산술평균, 그리고 기하평균
고등학교에서 배우는 아주 중요한 부등식이 하나 있습니다.
바로 산술-기하평균 부등식인데요,
산술평균이 기하평균보다 언제나 더 크다는 것 입니다.
산술 평균이란, 우리가 평소에 사용하는 평균으로
각각의 값을 더한 뒤, 개수만큼 나눠주는 것입니다.
기하 평균이란, 곱에 대한 평균이라고 생각할 수 있습니다.
각각의 값을 곱한 뒤, 개수만큼 거듭제곱근을 취해주는 것입니다.
두 개의 수 a, b가 있을 때,
산술평균은 (a+b)/2 이고, 기하평균은 √ab 가 되겠습니다.
산술-기하평균 부등식의 증명은 완전제곱식을 이용해서 할 수 있습니다.
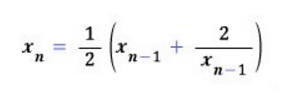
바빌로니아 방법을 바라보면
바빌로니아 방법에서 우변을 보시면,
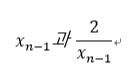
의 ‘’산술’’평균값임을 알 수 있습니다.
그런데, 두 값의 ‘’기하’’평균 값을 생각해보면,
그 값이 바로 루트2라는 것을 생각해볼 수 있겠습니다.
이 점화식은 두 값의 산술평균을 Xn값으로 사용합니다.
이것은 어떤 의미가 있을까요?
수직선위에 표현하면 다음과 같습니다.
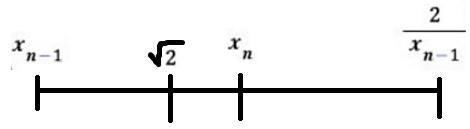
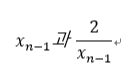
이 양 끝에 있다고 한다면,
산술평균인 Xn이 정중앙에 있겠고,
기하평균인 루트2가 그것보다 약간 왼쪽에 있게 됩니다.
이제 이 다음을 생각해보면,
Xn+1은 루트2와 Xn 사이에 있게 됩니다.
이 말은 Xn+1이 Xn보다 루트2에 가깝다는 뜻이겠죠.
따라서 바빌로니아 방법으로 근삿값을 구할 수 있게 되는 것입니다.
오늘은 바빌로니아 방법이 나오게 된 이유를
산술-기하평균 부등식과 관련 지어 설명해보았습니다.
바빌로니아 사람들이 ‘’기하’’평균에 대한 개념까지
있었다고 생각해볼 수 있겠습니다.
재미있게 보셨나요?
감사합니다.
ryanhan이었습니다.
로팀 당첨되셨네요!!! 축하드립니다!!!^,^
a post that is very admiring and very beautiful
바빌로니아의 추정연도를 생각하면 엄청난 문명이었죠. 그런 문명이 무색하게 멸망해서 과실은 그리스가 먹은것같지만....
짱짱맨 태그 사용에 감사드립니다^^
존버앤캘리 이번편은 왠지 찡함..^^
https://steemit.com/kr/@mmcartoon-kr/20180307
[골든티켓x짱짱맨x워니프레임] 10차 옴팡이 이모티콘 증정
https://steemkr.com/kr/@goldenticket/x-x-10-100
Your level lowered and you are now a Red Fish!
Congratulations @ryanhan! You received a personal award!
Click here to view your Board
Do not miss the last post from @steemitboard:
Congratulations @ryanhan! You received a personal award!
You can view your badges on your Steem Board and compare to others on the Steem Ranking
Vote for @Steemitboard as a witness to get one more award and increased upvotes!