Romans 8:28-30 – Logical Chain Argument
Romans 8:28-30
A logical chain argument, or, a Categorical Sorites.
Rom. 8:28-30 LEB
And we know that all things work together for good for those who love God, for those who are called according to his purpose,
because those whom he foreknew [i.e. Foreloved], he also predestined to be conformed to the image of his Son, so that he should be the firstborn among many brothers.
And those whom he predestined, these he also called, and those whom he called, these he also justified, and those whom he justified, these he also glorified.[1]
The logical deduction Paul uses here is called a Sorites. This is simply a normal bullseye syllogism (i.e. A.A.A, where A is a proposition that = All Subject is in the Predicate), but it continues to add additional categories, where the previous category is placed inside the next one. (All A is inside of B, and all B is inside of C; Thus, all A is inside the category of C.) What needs to happen is that the predicate of the previous proposition needs to be the subject of the next with affirmative propositions. This will create a circle diagram where one circle will be placed in the next. The circles do not lie; they give a visual demonstration of the deduction; to show if it is invalid or not. In this case, it is valid. Because this is a normal AAA bullseye type syllogism but only longer (i.e. A.A.A.A.A.), one is able (if the sorites is done correctly) to take any two premises and form an independent AAA syllogism.
There are exceptions for a particular premise, for a negative one, and when it is stated in the form of a hypothetical (If P, then Q) but that is for another time. Also, this type of syllogism may be stated in a reverse format. [2]
The form looks like this with a 6 premise sorites.
All A is inside the category of B
All B is inside the category of C
All C is inside the category of D
All D is inside the category of E
All E is inside the category of F
Thus, All A is inside the category of F.
A to F Sorites
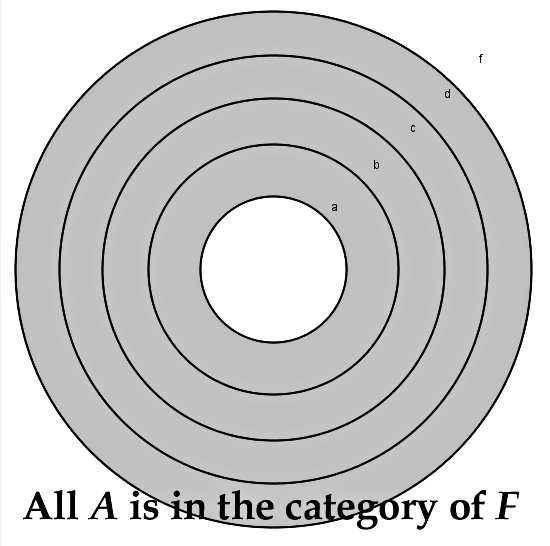
I see examples of other people mentioning this sorites in Romans 8:30, however, they are prone to leave out verse 29, and thus only make this a 4-premise syllogism. This is a mistake, because the first premise comes from verse 29; and thus, the syllogism is in fact 5 premises.
At any rate, the first premise starts with, Those whom God foreloved are those He predestined.” The rest of the verse gives us extra insight as to what this predestination results in for both Jesus and for the ones predestined; however, this is not relevant for the immediate syllogism being made by Paul, because the next verse simply picks up at the category of, “whom He predestined … .” The predicate of premise is the subject of the starting premise in verse 30. Paul does not give the conclusion of this syllogism. However, in my experience of reading Paul he normally does gives the conclusion. I suspect that he does not here simply because he so exactly spells out the rest of this enthymeme sorites that the conclusion it is not needed, for it is obvious.
In summary, we are told all things work for our good who are called by God in verse 28. Paul then gives a sorites to show the undeniability of this reality. We are told from the initial love of God to glorification the saints are directed by God’s decree to love them, and that this decreeing leads to a good end, without any falling through the cracks or mishaps. Whom God foreloves He glorifies. God direct and absolute sovereignty is the totality of all Christian metaphysics and ontology. Soteriology is in fact a sub-category under metaphysics. That is, it is how God uses existence and causality toward this particular group of elect persons.
Also, it is in this syllogism that Paul shows the reality of verse 28’s category of “the called.” Paul shows us that this category needs to be seen in the larger logical and metaphysical reality of God’s decrees. He desires for them to see it all put together in a chain argument. Here we find being “Called” is in the middle of the decreeing, and that the decree starts with being foreloved first, and then finally ends –without fail—being glorified with Christ.
See my book or article called, The Order of the Divine decrees to see how this fits together in an even larger view of the Divine Decrees. Foreloved would be in decree 2. Predestination would be decree 3. Called would be 8. Justification would be 9. And Glorification would be point 10.
(A) Those whom God foreloved are (B) those whom God predestined.
(B) Those whom God predestined are (C) those whom God called.
(C) Those whom God called are (D) those whom God justified.
(D) Those whom God justified are (E) those whom God glorified.
Therefore, (A) those whom God foreloved are (E) those whom God glorified.
Predicate Logic.
Chain syllogism Rule for Natrual Deduction

HCS = Hypothetical Chain Syllogism rule for Natural Deduction. (see pic)
Terms:
L = Foreloved. g = God. P=predestined. C = Called. J = Justified. G = glorified. s = Sally.
For every x, if x is fore-loved by God, then x is predestined by God; and, if x is predestined by God, then x is called by God; and if x is called by God, then x is Justified by God; and if x is Justified by God, then x is glorified by God.
- Ɐx (Lgx ⸧ Pgx) • Ɐx(Pgx ⸧ Cgx ) • Ɐx (Cgx ⸧ Jgx) • Ɐx (Jgx ⸧ Ggx )
- Lgs ⸫ Ggs
- (Lgs ⸧ Pgs) • (Pgs ⸧ Cgs ) • (Cgs ⸧ Jgs) • (Jgs ⸧ Ggs ) 1,2 UI
- Ggs 3. HCS