New Theory May Explain Why Neural Networks Work [Revised]
Machine learning has enjoyed many successes in recent years, surpassing milestones like beating Go champions at their own game, driving autonomous vehicles down busy city streets in the rain at night, recognizing different types of objects in digital photographs, recognizing words in spoken language, and generating translations from one language to another. But a somewhat disquieting notion about the whole enterprise has been lurking in the shadows for a number of years. To be honest, no one truly understands why it works.
To be sure, there are scores of online MOOCs, video college lectures, and research papers explaining how to construct any of the several types of neural networks. And there are indeed several variations, identified by a veritable alphabet soup of acronyms: CNN, RNN, LSTM, GAN, GRU, VAE, RBM, and so forth. But we don't start from a complete understanding of biological intelligence and build applications based on that. Work in the field has been largely experimental. For example, a researcher will take one of the old architectures of a neural network from the 1980s, make some structural changes to it, and then perform a series of experiments to ascertain whether the new construction achieves a faster learning rate or a higher task accuracy.
We know that neural networks have the ability to look at thousands of examples of a particular type of data (e.g., pictures of dogs, the details of past real estate sales, or a collection of speeches delivered in a parliamentary assembly) and then perform some mathematical magic to create generalizations from those specific instances. The generalizations enable the machine to make decisions about new data it hasn't seen before (e.g., identifying objects in a new photo, predicting the sales price for a house currently on the market, or generating a string of characters that looks like a plausible sentence).
But the precise reason why this method of computation works, and gives the semblance of intelligence, remains something of a mystery. When pressed on the question "why do neural networks do what they do," leading scientists will admit that this is still an open area for research.
So it created a stir recently at an AI conference in Berlin when a university professor announced that he may have an answer. Naftali Tishby, a computer scientist and neuroscientist from the Hebrew University of Jerusalem, maintains that deep neural networks learn because of a phenomenon he calls the “information bottleneck." According to Tishby, a neural network continually gets rid of "noise" in the input data. At each layer of the network, the learning algorithm eliminates extraneous details that are not relevant to a general principle, as if by squeezing the information through a bottleneck.
This could very well be a fundamental idea for intelligence and learning. Whether you’re a human being, or a jellyfish, or a mathematical algorithm, Tishby states that “the most important part of learning is actually forgetting.”
The video of Tishby's talk at this conference is included below. It presumes a certain level of knowledge about the subject, so if you're not already familiar with concepts like Markov chains, information entropy, and stochastic gradient descent, the material might appear to be quite rigorous. However, the goal of this Steemit article is to provide some background and make Tishby's theory more accessible.
Credit: "Deep Learning: Theory, Algorithms, and Applications," Berlin, June 2017
What Was Old Has Become New Again
In the interest of full disclosure, the "information bottleneck" idea isn't really new. It dates back to some of Tishby's earlier work from years ago, especially a collaboration in 1999 with Fernando Pereira and William Bialek (see https://arxiv.org/pdf/physics/0004057.pdf).
The 1999 paper attempts to lay a mathematical foundation for the information bottleneck concept. But it has a rocky start, dealing out some slights against Claude Shannon, the widely respected founder of information theory back in the late 1940s. To paraphrase Tishby, Shannon was only concerned with the communication of information, not on its effects upon the receiver of the information. And because information theory became so dominant in academia, people in the field never applied the mathematics and tools of information theory to our common sense notions of "meaning" and "relevancy."
This claim is a bit clumsy, if not overbroad. It's true that information theory got its start by answering such questions as the amount of information that can be pushed through a noisy communications channel (e.g., a telegraph wire, an FM radio broadcast, a telephone wire). See A Mathematical Theory of Communication, C.E. Shannon (1948). And it is true that Shannon said that "[the] semantic aspects of communication are irrelevant to the engineering problem." But Shannon identified concepts and theories that have a direct historic connection to the AI machines we are building today.
For one thing, Shannon himself gave us the notion of information entropy, which he analogized from statistical thermodynamics. Entropy is a measure of the amount of uncertainty involved in the value of a random variable or the outcome of a random process. For example, if you flip a coin, there is one of two possible outcomes. The act of flipping the coin has less entropy than rolling a die, since the die has six possible outcomes. Entropy is associated with the amount of information communicated. If we eliminate one coin side, we communicate less information that if we eliminate five sides of die. Information entropy, Wikipedia.
Information theory also gives us the notion of cross entropy, which is fundamental to the construction of certain neural networks, especially those that solve classification problems. Examples include: identifying an image as belonging to one of a number of animal classes (dog, cat, bird), or identifying whether a particular EKG matches one of a number of heart rhythms indicating a disorder or illness.
Cross entropy enjoys a solid historical line in the academic literature all the way back to Shannon's seminal work. We could start with Hinton and others, who recognized the value of cross entropy when talking about deep belief nets. See A Fast Learning Algorithm for Deep Belief Nets, Geoffrey Hinton, Simon Osindero, and Yee-Whye Teh, 2006. Taking a step back, Shore and Johnson treated cross entropy as being synonymous with KL minimum directed divergence in their work. See Axiomatic Derivation of the Principle of Maximum Entropy and the Principle of Minimum Cross-Entropy, John Shore and Rodney Johnson, 1980. And taking one more step back, Kullback and Liebler drew inspiration for their minimum directed divergence from the formulas in Shannon's 1948 paper. See On Information and Sufficiency, S. Kullback and R. Leibler, 1951.
A Brief Review of Neural Networks
Let's review neural networks by briefly considering the layout of a multilayer perceptron, which has a rather simple structure. An example is shown in the diagram below.
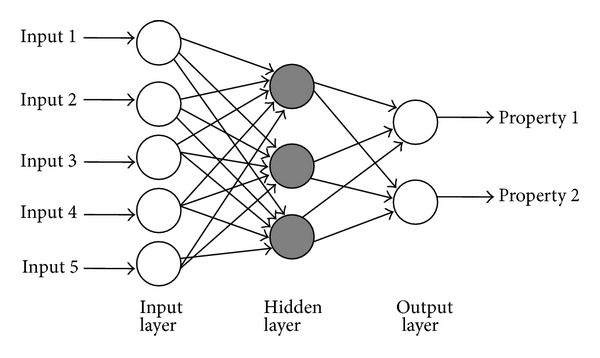
Each node in the diagram represents the idea of a neuron. A neuron consists of a weight, a cell value, an activation function, and an output value. It's biologically inspired (based on neuroscience circa 1980) to the extent that one can imagine an input signal (perhaps an electrical voltage from the retina) traveling along a dendrite, entering the neural cell and changing the voltage within (as modified by a weighted value), and then building up there until an activation threshold is reached. The output electrical voltage is discharged from the cell and travels down the axon. All of this is simulated with math: the input is multiplied by the weight and then supplied to an activation function to determine the output value. Popular activation functions include the sigmoid and rectified linear unit (ReLU).
As shown in the diagram, the neurons are arranged in layers. The neurons in the first layer are connected to every input signal, but not to each other. Consequently, each neuron in the first layer receives every input signal, as modified by the appropriate weighted value. These weights have the intuitive effect of increasing or decreasing the signal strength. The value is stored in the cell and then supplied to the activation function. The result is then passed as a new input to the next layer of neurons. Incidentally, we can optimize the processing of all of these multiplication operations using matrix multiplication. One matrix stores the input signals, and another matrix stores the weights.
The outputs are passed to the next layer, and the process repeats. At the final step, we perform an evaluation of all of the output signals to arrive at a predicted output value. During supervised training, we know what the model should have predicted because we know the real world value for this set of inputs: perhaps the inputs represented the pixel image of a dog. We apply a cost function to determine how far the predicted value strayed from the "right answer," and then distribute the error backwards through the network in a process called backpropagation. Each weight is adjusted upward (rewarded) or downward (punished) based on the extent to which that particular weight contributed to the final prediction.
And this is basically how a neural network "learns." We take a massive set of training data (e.g., pictures of animals), where each sample contains all of the input values (e.g., pixel values) as well as the "correct" output value (e.g., a string label identifying the type of animal), plug each sample into the network, and then perform backpropagation to adjust the weights.
Incidentally, a better architecture for classifying digital images is the convolutional neural network (CNN). However, that architecture would have introduced a level of complexity that is not required to understand Tishby's theory.
Peering Inside the Black Box
We would like to know what's going on inside of a neural network--what is making it learn. But you can't just open it up and watch gears turn. The "gears" are mathematical transformations on numeric data. We have a fuzzy, general idea that a neural network identifies "features" from the input data. Features are parts of an image that are generally shared across other similar images. For images of the number "9", one feature could be the closed loop at the top of the symbol. For images of a dog, a feature could be part of a pointy ear, or wet nose, or paw.
If you train a convolutional neural network (CNN) on different types of images, you will see a pattern develop in the early layers. Each of the neurons in the first layer appears to identify edges (i.e., transitions from a dark area to a light area). The second layer will look like it's morphing the features from the first layer together, somehow. But as we go through layers 3 and beyond, all bets are off. We honestly cannot tell what the machine has identified as higher-level features, and things get more strange the deeper you go into the network.
One approach, of course, would be to add code to the network that collects some sort of statistic during training. For example, we always capture and plot the values coming out of the cost function. By review, we use a cost function in supervised training to measure how far off the network's prediction is from the real world observation. We create an equation based on cross entropy, and then repeatedly try to minimize it. That is, for every batch of data read into the network, we determine the error and distribute it back through the network, layer by layer, and adjust all of the neural weights via backpropagation.
So error is an important statistic. We plot the error as is changes from batch (epoch) to batch. Now what?
The Core Ideas in Tishby's Theory
In Tishby's view of things, we take a step back and view each layer as an entity. One could view it as an affine transformation of the inputs from the previous layer, but Tishby views it as a partition of the original information. Each layer represents some clump of information. As such, he would assign a variable to each layer: the input layer is X, any of the successive layers which apply weights (typically called hidden layers) is an H, and the output layer is Y.
As Tishby trained neural networks over and over again, he looked at the amount of information being stored in each layer (in each variable). He looked at the mutual information shared between one layer and the next. In information theory, the mutual information of two random variables is a measure of the mutual dependence between the two variables. In other words, this concept measures the information that X and Y share. It measures how much knowing one of these variables reduces uncertainty about the other. For example, if X and Y are completely independent, then knowing X does not give any information at all about Y, and vice versa, so their mutual information is zero. In that case, we would say that I(X; Y) = 0.
We can also think of mutual information in terms of entropy. That is, the mutual information between random variables X and Y is the same as the entropy of X minus the conditional entropy of X given Y. We would write this in formula form as I(X; Y) = H(X) - H(X | Y). That is, the mutual information between these two variables is equal to the amount of uncertainty in variable X that is removed once you know the information in variable Y.
And this idea about mutual information led to an interesting observation: the amount of mutual information between one layer (H1) and the next (H2) always decreases as a neural network is trained. Also, for the purpose of making the final prediction, the only layer that is important is the final layer (Hn).
Further, Tishby also found that two statistical measures (and only two) effectively capture the learning behavior of the network:
- Sample complexity.
- Accuracy (generalization precision).
Sample complexity measures how many samples of input data are needed during training to achieve a certain level of accuracy. Tishby's experiments revealed that this measurement is completely determine by the amount of mutual information between the input layer (X) and the last hidden layer (Hn). Tishby refers to this portion of the network, from X to Hn, as the "encoder." Mathematically, we say that: Complexity = I(X; Hn).
Accuracy, also known as generalization precision, measures the probability that the network will make a correct prediction of output value when it encounters new inputs (inputs that it had not seen during any training). The network never saw these inputs before, and yet it can make a a correct decision/prediction anyway. And it dues this because it formed a generalized idea of what the training data represents. For example, it reads in a new digital image and predicts that it contains a horse. Tishby's experiments revealed something interesting about this statistic as well. Accuracy is completely determined by the amount of mutual information between the last hidden layer (Hn) and the final output (Y). Tishby refers to this portion of the network as the "decoder." Mathematically, we say that: Accuracy = I(Hn; Y).
Wouldn't be interesting if we plotted these two statistics as we trained neural networks?
Well, Tishby did precisely that. Starting about 13:44 minutes into the lecture video, Tishby shows an animation of this data. Sampling complexity is plotted as I(X; Hn) on the x-axis, and accuracy is plotted as I(Hn; Y) on the y-axis. Each data pointa point represents a separate training run using different initial conditions (most likely by using different nd by reading the training samples in different order). Data points sharing the same color represent measurements taken from the same layer in the network.
But Tishby didn't just train the network once. He ran the input data through the network multiple times. Each training run of the complete set of training data is referred to as an *epoch". Tishby treated the data plot from each epoch as a slide in an animation, which permits us to watch how sample complexity and accuracy change over time during a training sequence of thousands of epochs.
Putting the animation in motion, you can see that each of the data points on the graph migrates upward. This was completely expected. The mutual information shared between the last hidden layer and the output layer is increasing. And that means that, once the network has transformed a set of input data from layer to layer and has created the information in the final hidden layer, that's all you need to make a good prediction of the output value. Put another way, if the system is truly learning anything, accuracy should be on the rise.
And here is where things get interesting. After a large number epochs, the data points start a different migration, all shifting to the left. This behavior was unexpected and represents one of the major contributions from this research. Tishby interprets this migration as signifying that the network is compressing the data. In other words, it takes fewer and fewer bits of input data to make the logical jump from the information in X to the information in Hn. If it takes fewer bits of input data to make its decisions, the network must be throwing away noise--bits of information that are irrelevant to the predictions made by the network.
Toward the Higher Goal of Relevancy, Not Just Accuracy
Although neural networks have made great progress in recent years, there is no question that they are very slow learners. A neural network requires thousands of different images of dogs before it can reliably identify them in other photographs. Yet, a human child can perform the task after looking at just one photo. As we continue work on improving neural networks and their learning speed, it might be useful to monitor the statistics from Professor Tishby's information bottleneck theory as we train our prototypes. Rather than just striving for generalization accuracy, we might consider aiming for a higher goal: making decisions that maximize relevance.
@cryptohustlin has voted on behalf of @minnowpond. If you would like to recieve upvotes from minnowponds team on all your posts, simply FOLLOW @minnowpond.
As a follower of @followforupvotes this post has been randomly selected and upvoted! Enjoy your upvote and have a great day!
@minnowpond1 has voted on behalf of @minnowpond. If you would like to recieve upvotes from minnowponds team on all your posts, simply FOLLOW @minnowpond.
@originalworks
The @OriginalWorks bot has determined this post by @terenceplizga to be original material and upvoted it!
To call @OriginalWorks, simply reply to any post with @originalworks or !originalworks in your message!
To enter this post into the daily RESTEEM contest, upvote this comment! The user with the most upvotes on their @OriginalWorks comment will win!
For more information, Click Here!
Special thanks to @reggaemuffin for being a supporter! Vote him as a witness to help make Steemit a better place!
Congratulations @terenceplizga! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOP@eileenbeach has voted on behalf of @minnowpond. If you would like to recieve upvotes from minnowponds team on all your posts, simply FOLLOW @minnowpond.
@royrodgers has voted on behalf of @minnowpond.
If you would like to recieve upvotes from minnowponds team on all your posts, simply FOLLOW @minnowpond.