[math,computation] Riemann geometry: Ricci scalar written in metric explicitly

This is a English version of my former post
The purpose of this posting is to express Ricci scalar in terms of metric only. i.e., derive
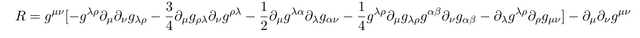
Convention
Define Covariant derivative as follows
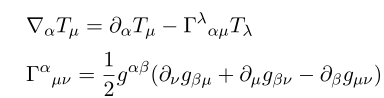
Under this convention we can define Riemann tensor as follows
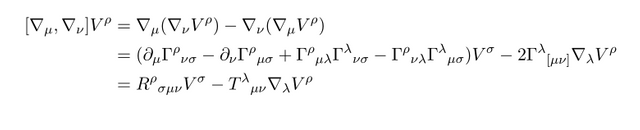
Note that T term be vanishes due to torsion-free condition.
From this we can define Ricci tensor and Ricci scalar as follows
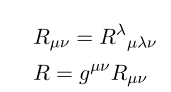
Computation
Now let's compute
First express Ricci scalar in terms of connection
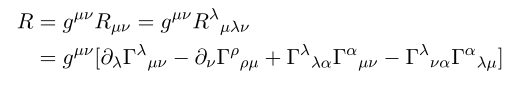
and the form of connection is given as
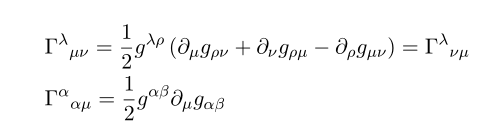
[The derivation of this connection was post in Korean in this post, since i use different notation, i did not translate it into English, but you can follow the math equation and get hints]
Now let's plugging in

Note that the red term get doubled due to the symmetric properties of metric g.
For blue terms re-ordering terms properly,
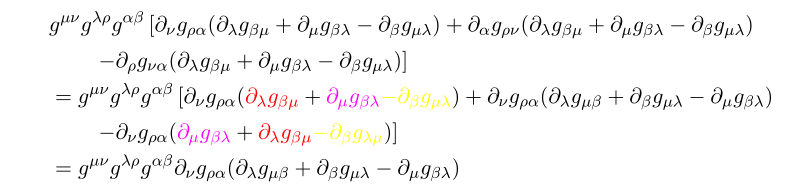
at this case each colored term cancel out.
And the purple term in the long computation of R reduces to
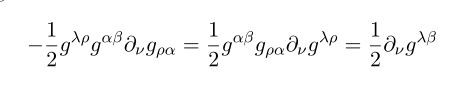
Now Let me keep doing this
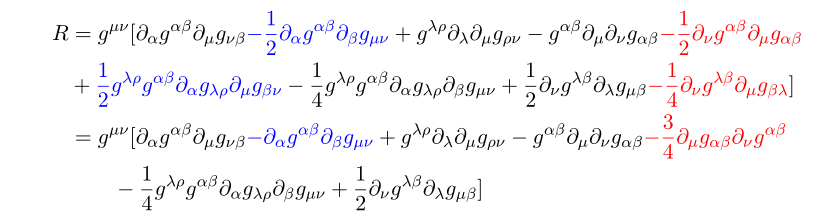
Note in the process we used

Now we are almost done. To make the desired form we need

with this, finally we obtain
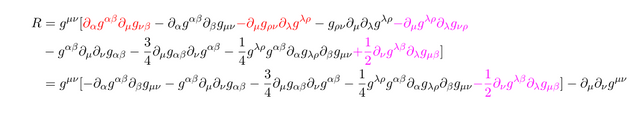
I am not sure where this equation comes from, i think i saw this equation from French Mathematician's textbook, which i am not sure of it. Anyway this equation is written in some parts of my notes, so i tried to derive.
Anyway i want to leave my effort in somewhere.
Thank you for your post.
Congratulations @beoped! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOPThis is a good complement to Leonard Susskinds lectures on general relativity, as he skips the above details.