Sophism #15: All Triangles are Isosceles
Consider an arbitrary triangle ABC. Let G be the midpoint of AB and let D be the intersection of the midpoint perpendicular of AB with the bisector of ∠C. Drop perpendiculars DE and DF to the sides AC and BC correspondingly.
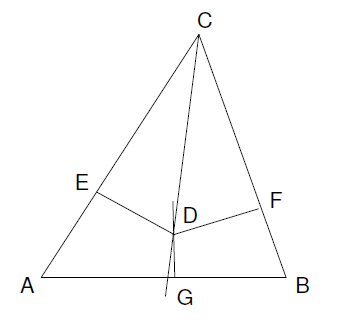
Now observe that, because CD is a bisector,
DE = CD sin(∠ECD) = CD sin(∠DCF) = DF (2)
Next, consider the triangle ADB. As DG is both a median and a height in this triangle, it must be isosceles, and thus DA = DB. From the equalities DE=DF and DA=DB follows the equality of the right triangles AED and BFD. Consequently:
Finally, add equations (1) and (3) together to obtain:
AC=BC
In other words, ABC is an isosceles triangle.
For other sophisms check out my other posts.