Paradox is fun! #2 - Will you switch the door? 趣味悖論 #2 - 你會換另一道門嗎?
The Game Time! 遊戲時間!
Imagine that you are participating in a game show. There are 3 doors in front of you. Only 1 of the 3 doors has a Benz behind while there is nothing behind the other 2 doors. The host asks you to choose to open 1 of the doors only and you can get the Benz if you open the right door. You then choose Door 1. When you are ready to open that door, the host stops you and he opens one of the other 2 doors for you to see, which shows nothing behind that door. The host now offers you a chance to switch to another door. Here comes the question:
Will you stay with Door 1, or will you switch to another door?
想像一下你在玩一個遊戲節目。你面前有三道門,當中只有其中一道門的背後有輛奔馳,而其餘兩道門後面都是空的。主持讓你從三道門中選擇去開一道門。如果你的運氣好的話,你就可以得到那輛名車。你隨便選擇了第一道門。當你想開門之際,主持人叫停了你並打開了另一道門給你看。裡面甚麼都沒有。這時候主持人給你一個機會: 你可以改為選擇另一道門。現在問題來了:
你會維持現狀選擇第一道門,抑或會改選另一道門?

The Monty Hall Problem 蒙提霍爾問題
The interesting paradox above is the well-known Monty Hall Problem. The name of this riddle is somehow due to the original host of the American television game show "Let's Make a Deal", namely Monty Hall.
這個有趣的悖論正是有名的蒙提霍爾問題。由於這個遊戲是源於一個美國電視節目"Let's Make a Deal"而最初的主持人叫蒙提霍爾,因而得此名。

Monty Hall in the 1970s 七十年代的蒙提霍爾
(Image 圖源: https://en.wikipedia.org/wiki/Monty_Hall)
Will you switch the door? 你會換另一道門嗎?
Most people, intuitively, will think that it makes no difference to switch the door or not. However, this is WRONG!!! Switching to another door will double your chance to get the nice car! How is that possible?
很多人會直覺地認為換門與否並沒有分別。然而,這是完全不正確的! 轉而選擇另一道門會讓你有兩倍機會獲得那輛名車! 這有可能嗎?
The Simple Maths 簡單數學
If you know elementary statistics, you can solve this problem using Bayes' Theorem. But let's put it in the simplest way by drawing a simple table as follow.
如果你知道一些基本統計學,你可以運用貝葉斯定理。以免簡單複雜化,讓我們用一個簡單的表格去解答這個問題。
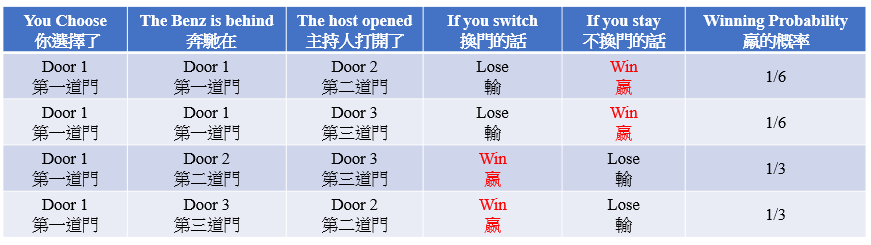
We can consider several different cases. In the first scenario, the Benz is really behind your door, i.e. Door 1. The host is equally likely to open Door 2 or Door 3 for you to see. If he opens Door 2 and you stay with your initial choice, you win and this event has a probability of 1/6. Why? Because the host chooses to open Door 2 with a chance of 1/2 and the chance of the Benz behind Door 1 is 1/3. It follows that the probability of the event in Row 1 is 1/2 * 1/3 = 1/6. Similarly, the probability of the event in Row 2 is 1/6 as well.
我們可以考慮幾個情景。在第一個情景中,假設名車在你選擇的門後面,亦即第一道門後面。那麼主持人有一半機會開第二道門或第三道門給你看。如果他開第二道門而你維持第一道門的選擇,那麼你就得到名車。而這個情況發生的機會率是1/6. 原因是主持人開第二道門的機會是1/2而名車在第一道門後面的機會是1/3,因此得1/2 * 1/3 = 1/6。如果他開的是第三道門而你的選擇不變,那麼我們可以相同的邏輯推論。
Consider another case where the Benz is behind Door 2. In this case, the host is forced to open Door 3 for you to see (Otherwise he will let you see the Benz). If you switch the door, you will win. The event happens with 1/3 of the time because the chance that the Benz is behind Door 2 is 1/3 and this time the host must choose Door 3 to open so there is no randomness here. The logic is the same for the event in the last row.
另一個情況,假設名車在第二道門的後面。那麼,主持人必然是要打開第三道門 (不然他就會讓你看到名車在第二道門的背後)。這個情況發生的機會率是1/3,因為名車有1/3的機會在第二道門的後面,而且主持人是強制性要開第三道門而並非隨機。同樣地上表的最後一行也以相同邏輯推論。
To conclude, the winning probability of a switch is 1/3 + 1/3 = 2/3 (Third and fourth row of the table) while the winning probability of keeping the initial choice is only 1/6 + 1/6 = 1/3 (First and second row of the table)!
因此,如果轉選另一道門,嬴的機會率為1/3 + 1/3 = 2/3 (表第三及第四行)。如果維持不變,嬴的機會率則只有1/6 + 1/6 = 1/3 (表第一及第二行)!
What causes the illusion? 為何我們會有錯覺?
It is natural to think that it makes no difference to choose another door or not. But what drives us to think in this way? Note that the host has full information of where the Benz is. By taking into account the information given by the host, this game is no longer fair in nature. I think no one will disagree that your initial choice must be wrong 2/3 of the time. In other words, the Benz is behind one of the 2 other doors 2/3 of the time. Now the host opens one empty door for you. If you switch to another door, it's like you choose the other 2 doors at the same time, with 2/3 of the time being right! It's the negligence of the information from the host that leads to the illusion of a half-half winning chance.
我們很自然會認為轉門與否沒有分別。但為何我們會有這種錯覺? 主要原因在於主持人是知道車在哪裡的。如果考慮主持人給的資訊,這個遊戲便不是一個公平的遊戲了。我想大家也同意自己原來的選擇有2/3機會是錯的。換句話說,名車有2/3的機會在其餘兩道門的其中一道背後。現在主持人給你打開一道空門,同時如果你轉為選擇另一道門,那麼情況就好似你同時打開2道門一樣,有2/3機會是正確的! 所以錯覺其實是源於一般我們會忽略了主持人給的資訊。
I write articles on machine learning, applied statistics, maths and economics to the best of my knowledge. If you like my posts, please upvote, resteem and follow me @manfredcml!
CN區的朋友大家好! 如果喜歡小弟的文章,可以upvote, resteem或follow @manfredcml支持!
English articles 英語文章:
Be a smart gambler! #1 - Gambler's fallacy
Let's play a game #1 - Prisoner's Dilemma
Paradox is fun! #1 - Boy or Girl?
No solution! #1 - Prime numbers
Everyday Tech Series
Bilingual articles 雙語文章:
Welcome to the world of mahjong! 歡迎來到麻雀教室! #1
No solution! #2 - P vs NP Problem / 無解 #2 - P vs NP問題
Here comes the monty hall problem! This one is a must-known for all statistics major students and the situation is just very counter intuitive which makes it interesting. The great lesson we can learn from the problem is that our intuitions could lead to fallacy if we do not build a good foundation in mathematics and this means a great loss, especially when we're always surrounded by numbers!
Yes this problem is really an interesting paradox in applied statistics. Many classes of elementary statistics will touch this simple yet confusing problem . If someone is learning Bayes' Theorems or related concepts abt conditional probabilities, this example will be a good illustration.
True. Back then when I was a student conditional probabilities and distributions were the first few topics to learn and in studying the topic actually there were lot more other confusing problems than the monty hall. Remind me of those days long ago!!
Seem like you are also a statistics major! To me, some statistical concepts are quite counter-intuitive but share really cool ideas. Like when we want to compare the number of points in [0, 1] and [0, 1] x [0,1], the latter is similar "larger" in some intuitive sense but they contain the same infinitely many points. So this partly leads to studies of measure theory which defines sizes in strictly math sense.
yes i'm a statistics major. But I didn't really touch the measure theory.. that sounds interesting. Do you have more to share about it as an introduction? Maybe you would want to write the next post on it, giving some examples and applications. That'd be great!
yes I have come across this problem in my University study as well. it's really a confusing problem when I first read it! but it's really interesting. I think probability is really one of the most interesting topic in maths.
that's really interesting! thanks for you great effort in writing this article!
Thanks for your support!
you are welcome! keep it up
Great article. The Monty Hall problem is very entertaining when discussed in groups, due to its counterintuitive nature.
Thank you for your support. Ya when I heard of this problem for the first time it would be really confused but when would soon realize that there must be something wrong and then tried doing the math! I always think math paradoxes are really interesting when sometimes our so-called intuition is not logically valid.
Very interesting.