[CS and Math #21] Matrix Multiplication - Strassen's Algorithm
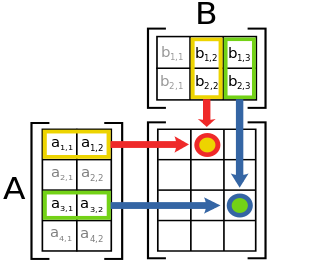
[1]
Matrix Multiplication Technique
Difficulty of Matrix Multiplication
Simply, a matrix is nothing but rectangular array of numbers. We say a matrix has
rows and
columns if it is of the form
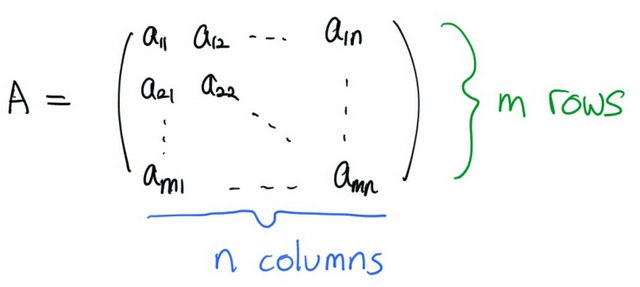
Now suppose we have two square matrices both of size
. What we want to calculate is the product,
which is another matrix. We can directly calculate
using the definition of matrix multiplication. If we denote the entries of
as
, then
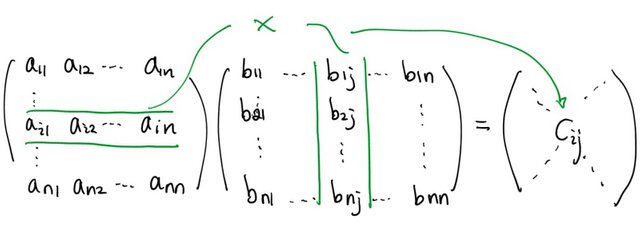
which can be expressed as formula
As many of us are familiar with four basic arithmetic operations; +, -, x, and /, it is reasonable to assume that these four basic operations are unit operations , which are fundamental and indecomposable operations. This brings up a question,
First, for an arbitrary entry ,
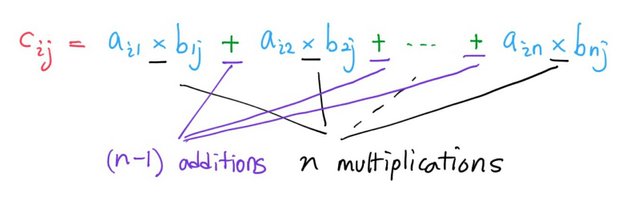
we need unit operations, so that in total,
number of unit operations for multiplying two square matrices. (Because there are
number of entries in
matrix)
Some say this is reasonable, but when gets large, the dominating term
diverges in fast speed, so that only supercomputers can handle them.
Obvious Lower Bound
We already proved that the obvious upper bound is , now what is the obvious lower bound for matrix multiplication? If there are no additional information about
, we need to examine all the entries (at least!). Each entry of
need at least constant number of unit operations, so this gives an obvious lower bound of the form
where is a constant.
Between Upper and Lower bound
So what we are trying to seek is a matrix multiplcation algorithm which has total number of unit operations between and
. At first, you might think that any matrix multiplication algorithm must have at least as much unit operations as obvious upper bound. But in 1969, German mathematician Volker Strassen published a remarkable algorithm for matrix multiplication that runs in
time, or in equivalent form, the number of unit operations satisfies
for large enough , where
are constants. It is clear that
for large enough
Strassen's algorithm
To keep things simple, let be a power of 2. If not, pad
number of zeros to matrix
where
is an unique integer satisfying
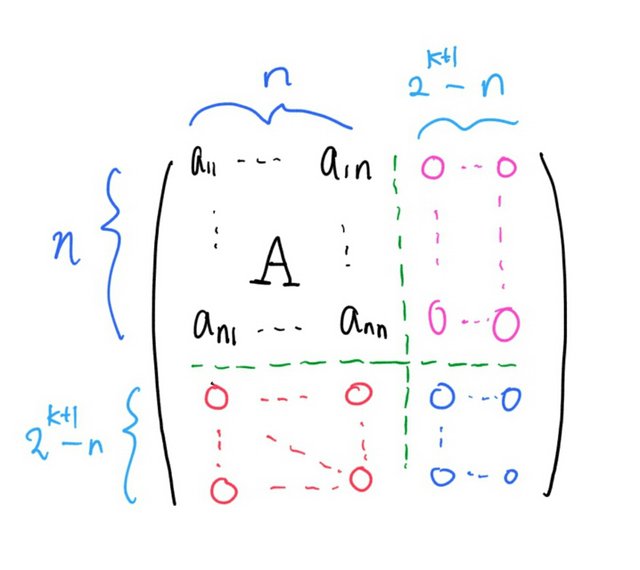
First Step
We divide each into four submatrices, as follows.
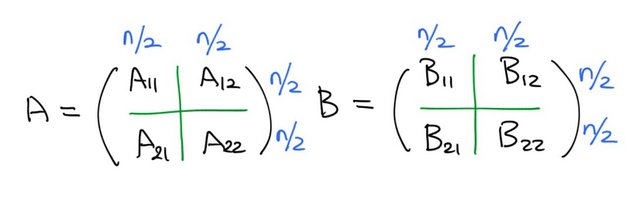
Now, the result would be
Second Step
This is the hardest and clever part, but it is straightforward. Create 7 matrices
Note that all submatrices have size so that additions, subtractions, and multiplications are indeed well defined.
Creating Output
From 7 matrices, we need to obtain submatrices . Look carefully.

so that .
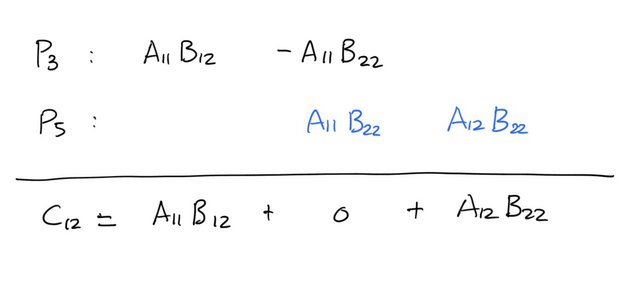
so that .
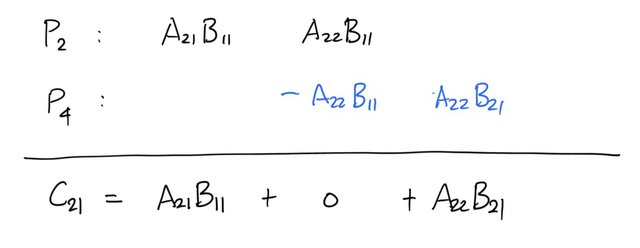
so that . Finally,

so that . Thus we've created all the entries of
using 7 submatrices.
Algorithm Analysis
Let's count how many unit operations were used in each step. Denote as the total number of unit operations on multiplication of
.
First Step Revisited
Dividing matrices does not require any operations (instead, it needs memory of course)
Second Step Revisited
is obtained by adding two
matrices twice and multiplying them each other. Addition of two
matrices needs
number of + operations, and also we need to recursively call Strassen's algorithm for multiplication, which is nothing but .

There are 3 matrices of this form, .
is obtained by single addition and multiplication.
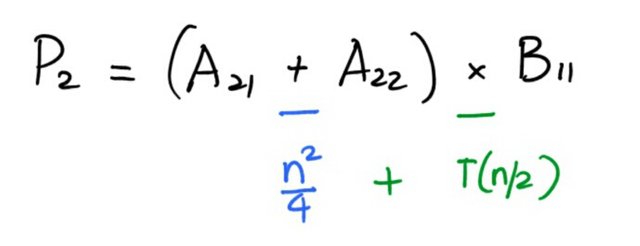
There are 4 matrices of this form, . In total,
number of operations are needed in second step.
Final Creation Step Revisited
Therefore, in this step, we need
number of unit operations.
Total sum
Adding up,
How do we solve this?
Let for some positive integer
. Then
solving the last equation gives
using geometric series formula. grows faster than
, therefore
as desired! The padding of zeros, does not affect the result, since padding increases memory requirements, not number of operations.
Example
For those who do not believe the result, let's look at particular example,
we get
matches with direct computation
Limitations
For practical reasons, Strassen's algorithm is often not the choice of matrix multiplication.
It uses a lot of memory. At each step, it produces 7 different submatrices, which is huge waste of memory.
Algorithm itself is numerically unstable. If all the entries are integers (or at least fractions), the multiplication has no error. However, due to limited precision of computer arithmetic on irrational numbers, larger errors accumulate
Conclusion
Theoretically faster but not practical enough. Still, it was a great breakthrough in matrix multiplication algorithm!
Citations
[1] Image source Link Creative Commons Attribution-Share Alike 3.0 (commercial usage allowed)
[2] Introduction to algorithms 3rd edition, Chapter 4, Section 4.2
[3] All other images are self made
Lastly I will post my implementation of Strassen's algorithm using MATLAB
function C = strassen( A, B )
[n, m ] = size(A);
% Base case
if n == 1
C = A(1,1) * B(1,1);
else
% Recursive Case
n = n / 2;
A11 = A(1:n, 1:n);
A12 = A(1:n, (n+1):end);
A21 = A((n+1):end, 1:n);
A22 = A((n+1):end, (n+1):end);
B11 = B(1:n, 1:n);
B12 = B(1:n, (n+1):end);
B21 = B((n+1):end, 1:n);
B22 = B((n+1):end, (n+1):end);
% Compute P1 to P7
P1 = strassen(A11 + A22, B11 + B22);
P2 = strassen(A21 + A22, B11);
P3 = strassen(A11, B12 - B22);
P4 = strassen(A22, B21 - B11);
P5 = strassen(A11 + A12, B22);
P6 = strassen(A21 - A11, B11 + B12);
P7 = strassen(A12 - A22, B21 + B22);
% Compute submatrices of C
C11 = P1 + P4 - P5 + P7;
C12 = P3 + P5;
C21 = P2 + P4;
C22 = P1 - P2 + P3 + P6;
C = [ C11, C12; C21, C22 ];
end
end


Great knowledge as always, both addition and subtraction of two matrices are really very simple, but multiplication is not so much easy, but you made it is easy, thanks for sharing such a great knowledge.
Thank you