[Math & Physics #12] The Harmony - Kepler's Third Law [Part 3]
[1]
Kepler's Law of Planetary Motion [Part 3]
This will be the last talk about Kepler's Law of Planetary Motion. Last two posts,<Math and Physics #10> and <Math and Physics #11> were about Kepler's first and second law. Today, I'm gonna talk about the third law, which states about the relationship between orbital period and semi-major axis of orbit.
0. What is Kepler's Third Law?
It states that
The square of the orbital period of a planet is proportional to the cube of the semi-major axis of its orbit.
Formally, a planet revolving around the sun with semi-major axis and period
obeys the following law.
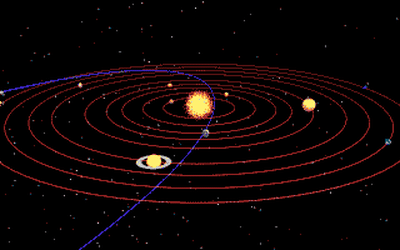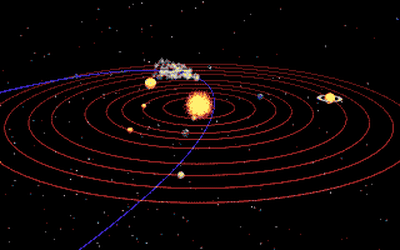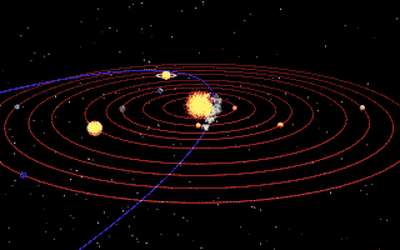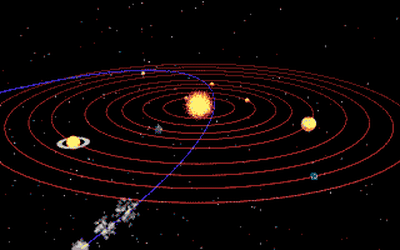
That is, as the orbit gets larger, the length of 1 year in that planet, gets longer. The following diagram shows the orbit of 5 planets - Mercury, Venus, Earth, Mars and Jupiter. As you can see, planets that are close to the sun revolves extremely fast. On the other hand, Jupiter; far away from the sun, revolves in slow pace.
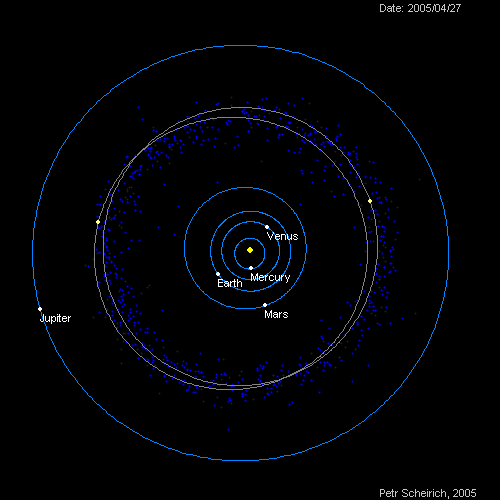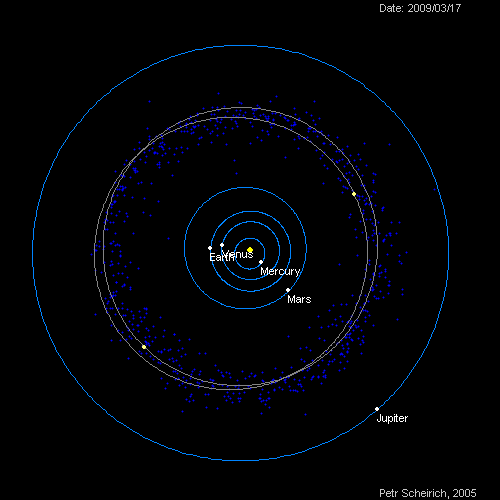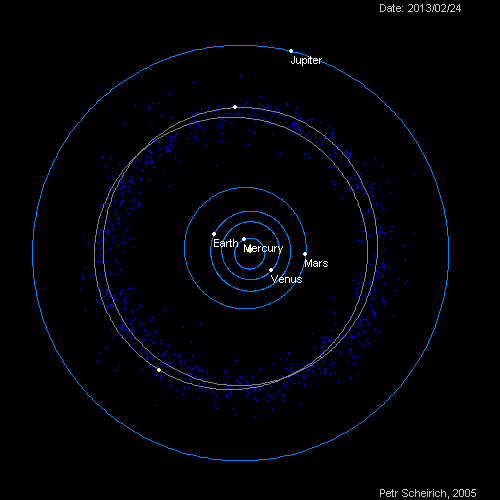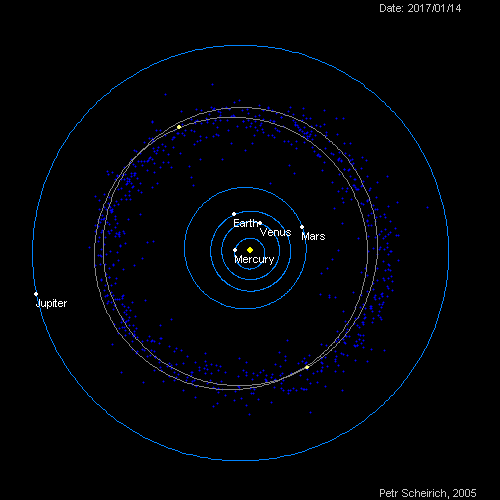
[2]
1. Why is it Important?
Kepler's third law was first published in 1619, on his paper <Harmonices Mundi>. It was about 10 years after his discovery of first and second laws. During that period, Kepler worked on finding the ultimate law of harmony of the sky using his first and second law of planetary motion. Although Kepler was not able to prove it mathematically, he was confident on his discovery of the relation
. Later, Newton - the giant - not only proved it but also found the actual proportionality constant hidden under the relation, which was
where are gravitational constants and mass of the sun respectively. Thus, if we neglect the gravitational force between the planets , the proportionality constant is independent of the variables related to specific planets. So, all the planets - Mercury to Neptune, will have same period to axis ratio,
.
2. The Law of Harmony - Verification
In order to verify Kepler's third law of motion, we need previous facts about first and second law as well as basic geometric facts about ellipse. First let's look at the diagram below.

The sun is fixed at the origin, and the planets is on elliptical orbit with semi-major axis and eccentricity
.
Kepler's first law states that the equation of the orbit in polar form is
Kepler's second law states that the rate of change of area swept by the vector respect to time is constant, so that
and we also obtained formula for speed respect to the distance by
Total Area of an Ellipse is given by
Now it's time for derivation. Distance between the sun and the planet when the planet is located at axis is given by
Also, so that
Now the area swept by the vector during one period
is equal to the total area of ellipse
. This gives
Using Newtonian mechanics, we get the proportionality constant, soley dependent on gravitational constant and mass of the sun, which is
3. Application to our Solar System
Orbital Characteristics of planets in our solar system are as follows. - [3]
| Name | Semi-major axis (AU) | Orbital Period (years) | Orbital eccentricity |
|---|---|---|---|
| Mercury | 0.39 | 0.24 | 0.206 |
| Venus | 0.72 | 0.62 | 0.007 |
| Earth | 1 | 1 | 0.017 |
| Mars | 1.52 | 1.88 | 0.093 |
| Jupiter | 5.2 | 11.86 | 0.048 |
| Saturn | 9.54 | 29.46 | 0.054 |
| Uranus | 19.22 | 84.01 | 0.047 |
| Neptune | 30.06 | 164.8 | 0.009 |
Theoretically, the proportional constant should be
The real values are
| Name | Proportionality constant (year^2 /AU^3) | Error (= differnece with 1.001) |
|---|---|---|
| Mercury | 0.971021 | -0.02998 |
| Venus | 1.029878 | 0.028878 |
| Earth | 1 | -0.001 |
| Mars | 1.006433 | 0.005433 |
| Jupiter | 1.000367 | -0.00063 |
| Saturn | 0.999586 | -0.00141 |
| Uranus | 0.994035 | -0.00696 |
| Neptune | 0.999879 | -0.00112 |
Are these errors small enough to neglect? Well, at first you can think so because the error terms look small. It can be a good approximation if you are dealing with small periods of time. But if you are considering large periods of time (such as month, year,...) actual positions of planets differ greatly with the hypothesis . You should take interplanetary gravitational forces into account, which makes the problem extremely hard (actually there is no closed form expression for velocity and orbit.) See three body problem - [4] for more information.
4. Conclusion
Kepler's third law is astonishing in the sense that it describes the relationship between the orbital period and semi-major axis without any specific considerations to the planet itself. However, it only applies to planetary system with single planet. If someone is dealing with planetary system having multiple planets, they must consider perturbations due to interplanetary gravitational forces.
5. Citations
[1] https://gfycat.com/gifs/detail/SpitefulWiltedEasternglasslizard
[2] https://superstarfloraluk.com/2756447-Planets-Solar-System-Orbits-Animation.html
[3] https://en.wikipedia.org/wiki/Planet#Planetary_attributes
[4] https://en.wikipedia.org/wiki/Three-body_problem
All other derivations and geogmetric figures are made by myself using LATEX and GeoGebra.

This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!
Hi @mathsolver!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV