Why Mathematics-- and my first Steemit post.

I am a mathematics graduate student from the Philippines, and I figured out that this site is a good platform to dump my thoughts about mathematics (and possibly other geeky stuff). What I'm planning here is pretty much to regularly write about what I currently know about mathematics while trying to explain it to the general lay audience.

So what exactly do these math people do in particular, and why do some people bother to dedicate their lives to it? You might think we've already mapped out pretty much all of mathematics right? I mean, what could we possibly need to know more about numbers? Well, for starters, mathematics spans more than the concept of numbers. Some people actually refer to mathematics as the "formal study of patterns", and while patterns are predominant in numbers, we certainly do not only see patterns in numbers. Furthermore, we currently do not know everything about numbers. But just to demonstrate, let us first look at something that we do know about numbers, thus we'll define what a prime number is: it is simply any positive whole number p greater than 1 that cannot be divided by any other positive number except for itself and the number 1. For example, 7 is a prime number because it cannot be divided evenly by 2, 3, 4, 5, or 6, and it is divisible by itself, because 7 divided by 7 is just 1, and it is divisible by 1 because 7 divided by 1 is just 7. Similarly, 11, 13, 17 are primes. So we have a good idea of what primes are, and we will now state an important result about them: "for every positive number greater than 1, we can find a prime number that divides it". So for example, 6 can be divided by the prime 3 because 6/3=2, and similarly 25 is divisible by prime 5 since 25/5=5. We will use this fact, to prove that there are "infinitely many primes". To prove this, we are going to use a technique that is pretty well known among mathematicians, it's called "proof by contradiction", that is, we assume that something we are proving is false-- in our case, that there are only finitely many primes, and we should find a contradiction if we follow along this line of reasoning. So, if we assume that there are only finitely many primes, then we should be able to list it like so:

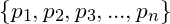
where 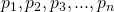are all the prime numbers that you can find. Now, we make another number using these primes, let's call it P, and define it like so: 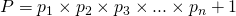which is the product of all our primes plus 1. Now, this is the important part of the trick, we can always write 1 as

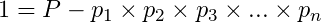
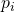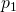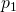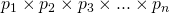We use our previous result, that all positive numbers greater than 1 can be divided by some prime, and since, we assumed that all our prime is contained in the list above, then P must be divisible by one of the 's in the list, and without loss of generality we can just assume that P is divisible by . Because P is divisible by and is also divisible by 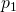, then 1, as the difference of two numbers which are divisible by 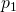, must also be divisible by the prime 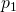. But 1 cannot be divisible by any prime number, because every prime number is greater than 1, therefore we have a contradiction, hence prime numbers cannot be listed finitely.

Even heroes fail

There you have it, that little piece of art above is what we call a proof, a bunch of statements stringed together by logic to arrive at a conclusion. If you made it until this point, I think you'll see that there is some exquisite beauty in proofs, that there is something elating about understanding a mathematical proof. Also, as a matter of fact, the proof above is pretty much the same proof that Euclid has shown thousands of years ago-- proofs transcend time, once found, they will always remain true for all eternity. This is what mathematicians really do, proving facts about mathematics-- not crunching really big numbers (some of them do that, but definitely not all), as some might think. Hence we go back to our first question, and I can say with confidence that this is the reason why some people are so hooked at math, it's just damn pretty.

Enough of my rambling, I hope you find my first post educational, and that you'll have a newfound appreciation of maths after this.