The Complex Number System: An Introduction

Our ultimate goal in this series of posts is to find all possible solutions for the nth roots of unity, and in general, for complex numbers. I anticipate this might take two or three posts, but we'll start from the basics in any case.
Background: The Fundamental Theorem of Algebra
The Fundamental Theorem of Algebra is a statement regarding the zeros of polynomial functions. It states that every polynomial P(x) of degree n has at least one complex root, and at most n solutions. Graphically, we equate these to the places where a graph crosses the x-axis. For example, if we graph
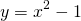 , we can very clearly see that the graph (the blue curve) crosses the x-axis at x = 1 and x = -1:
, we can very clearly see that the graph (the blue curve) crosses the x-axis at x = 1 and x = -1:
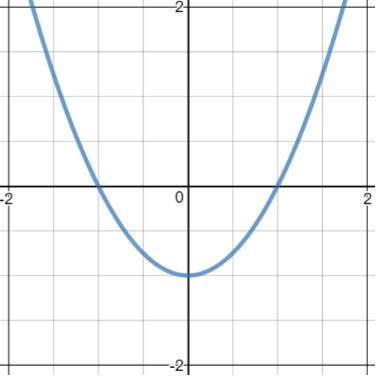
But what happens when you have a graph that doesn't cross the x-axis? For example, consider 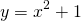 . If you try to solve it by hand you get
. If you try to solve it by hand you get 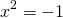 , and according to conventional wisdom, one can't have the square root of a negative number. This would seem to be a contradiction: in many functions, you can find roots simply by finding the intersection with the x axis, yet here, the graph misses it completely!
, and according to conventional wisdom, one can't have the square root of a negative number. This would seem to be a contradiction: in many functions, you can find roots simply by finding the intersection with the x axis, yet here, the graph misses it completely!
The Imaginary Unit
Around the 16th century mathematicians began to study higher order polynomials. Factoring had already been known to al-Khwarizmi in his famous algebra text, yet attempts to factor some higher order equations seemed impossible, even if irrational numbers were used, since it was required to take the square roots of negative numbers. For example, Niccolò Tartaglia had developed the method of solving certain cubic equations. Using his method, solutions to an equation like 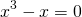 could be written with the rather unwieldly form:
could be written with the rather unwieldly form:
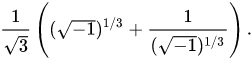
At the same time it was known that there were real solutions -1, 0, and 1 by factoring. Clearly, the square root of -1 must have had some mathematical meaning. Otherwise, it could not be possible to obtain a real number by manipulating it.
The solution, it turned out was simple enough. In order to solve 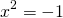 , it was simply necessary to extend the real numbers to include a definition of the square root of -1. In other words, one can simply define a new value, the imaginary unit, where
, it was simply necessary to extend the real numbers to include a definition of the square root of -1. In other words, one can simply define a new value, the imaginary unit, where 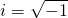 .
.
At first, this might seem a bit like "cheating," but it is in fact no less valid than using negative numbers to represent a financial debt. You might not be able to have a "negative five dollar bill", but you can certainly owe someone five dollars. Similarly, imaginary numbers are perfectly valid from a mathematical standpoint, and there are indeed real-world applications that use i, most notably electrical engineering and signal analysis. Complex numbers can also be used to produce beautiful fractals such as the Mandlebrot Set and the Julia Set.
Combining imaginary numbers with real numbers numbers, you can get complex numbers. Complex numbers can have the form 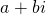 , where a and b are real numbers and i is the imaginary unit. We call a the real part and bi the imaginary part, and although they are joined by a plus sign, the entire value a+bi ought to be considered a single value, and not the sum of two values.
, where a and b are real numbers and i is the imaginary unit. We call a the real part and bi the imaginary part, and although they are joined by a plus sign, the entire value a+bi ought to be considered a single value, and not the sum of two values.
Representing Complex Numbers
Now that we know complex numbers exist, the question is on how to represent them. How can something that's "imaginary" be represented visually? If you recall your first grade math class, you had a number line that looked something like this:
Negative numbers went on the left, and positive numbers went on the right, and the number you wanted to plot went right on the line. When we represent complex numbers, we need some more space to show the complex part, so we add another dimension, and our "complex number plane" ends up looking like this:
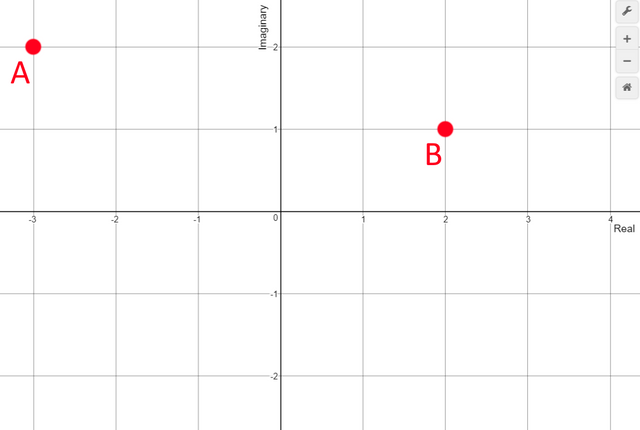
You can now plot any complex number as a coordinate, using the horizontal axis as the real axis and the vertical axis as the imaginary axis. For example, point A represents the complex value -3 + 2i, while B represents 1 + i. Keep in mind that even though we use the addition formula, they are really one single value rather than two.
Look closely at the complex plane. If I wanted to, I could draw a triangle to any point on the complex plane, using that point as the "tip" of the triangle and vertical and horizontal lines as legs. For example, to plot 3 + 4i, I could draw the following:
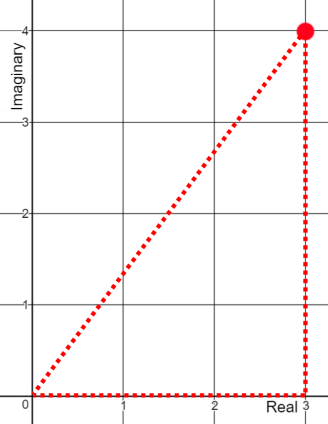
The angle between the slanted line is obviously atan(b/a), based on the definition of the tangent function and the length is 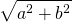 based on the Pythagorean theorem. We've now just defined the same point in terms of its angle and its distance from the origin. We call this the polar form of a complex number. Thus, to convert any complex number, a + bi, to its rectangular form, you can simply rely on trigonometry, and write:
based on the Pythagorean theorem. We've now just defined the same point in terms of its angle and its distance from the origin. We call this the polar form of a complex number. Thus, to convert any complex number, a + bi, to its rectangular form, you can simply rely on trigonometry, and write: 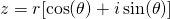 , where
, where 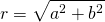 and
and 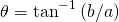 . We'll see why this is relavent in the next post.
. We'll see why this is relavent in the next post.
To be continued...
In the next post, we'll take a look at some of the operations on complex numbers, and then talk about how it ties in with the unit circle. In the meantime, you can look at @drifter1's take on complex numbers)
Good introductory on Complex numbers..!
U might want to conclude ur article a little better. May b some hints about next post or at least with some concluding thoughts.
Anyways, best regards...! 🙌
Nice introduction to complex numbers :)
Thanks for mentioning me!